Kaniadakis statistics (also known as κ-statistics) is a generalization of Boltzmann–Gibbs statistical mechanics,[1] based on a relativistic[2][3][4] generalization of the classical Boltzmann–Gibbs–Shannon entropy (commonly referred to as Kaniadakis entropy or κ-entropy). Introduced by the Greek Italian physicist Giorgio Kaniadakis in 2001,[5] κ-statistical mechanics preserve the main features of ordinary statistical mechanics and have attracted the interest of many researchers in recent years. The κ-distribution is currently considered one of the most viable candidates for explaining complex physical,[6][7] natural or artificial systems involving power-law tailed statistical distributions. Kaniadakis statistics have been adopted successfully in the description of a variety of systems in the fields of cosmology, astrophysics,[8][9] condensed matter, quantum physics,[10][11] seismology,[12][13] genomics,[14][15] economics,[16][17] epidemiology,[18] and many others.
Mathematical formalism
The mathematical formalism of κ-statistics is generated by κ-deformed functions, especially the κ-exponential function.
κ-exponential function

The Kaniadakis exponential (or κ-exponential) function is a one-parameter generalization of an exponential function, given by:
with .
The κ-exponential for can also be written in the form:
The first five terms of the Taylor expansion of are given by:
where the first three are the same as a typical exponential function.
Basic properties
The κ-exponential function has the following properties of an exponential function:
For a real number , the κ-exponential has the property:
- .
κ-logarithm function
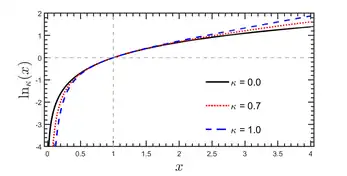
The Kaniadakis logarithm (or κ-logarithm) is a relativistic one-parameter generalization of the ordinary logarithm function,
with , which is the inverse function of the κ-exponential:
The κ-logarithm for can also be written in the form:
The first three terms of the Taylor expansion of are given by:
following the rule
with , and
where and . The two first terms of the Taylor expansion of are the same as an ordinary logarithmic function.
Basic properties
The κ-logarithm function has the following properties of a logarithmic function:
For a real number , the κ-logarithm has the property:
κ-Algebra
κ-sum
For any and , the Kaniadakis sum (or κ-sum) is defined by the following composition law:
- ,
that can also be written in form:
- ,
where the ordinary sum is a particular case in the classical limit : .
The κ-sum, like the ordinary sum, has the following properties:
The κ-difference is given by .
The fundamental property arises as a special case of the more general expression below:
Furthermore, the κ-functions and the κ-sum present the following relationships:
κ-product
For any and , the Kaniadakis product (or κ-product) is defined by the following composition law:
- ,
where the ordinary product is a particular case in the classical limit : .
The κ-product, like the ordinary product, has the following properties:
The κ-division is given by .
The κ-sum and the κ-product obey the distributive law: .
The fundamental property arises as a special case of the more general expression below:
- Furthermore, the κ-functions and the κ-product present the following relationships:
κ-Calculus
κ-Differential
The Kaniadakis differential (or κ-differential) of is defined by:
- .
So, the κ-derivative of a function is related to the Leibniz derivative through:
- ,
where is the Lorentz factor. The ordinary derivative is a particular case of κ-derivative in the classical limit .
κ-Integral
The Kaniadakis integral (or κ-integral) is the inverse operator of the κ-derivative defined through
- ,
which recovers the ordinary integral in the classical limit .
κ-Trigonometry
κ-Cyclic Trigonometry

The Kaniadakis cyclic trigonometry (or κ-cyclic trigonometry) is based on the κ-cyclic sine (or κ-sine) and κ-cyclic cosine (or κ-cosine) functions defined by:
- ,
- ,
where the κ-generalized Euler formula is
- .:
The κ-cyclic trigonometry preserves fundamental expressions of the ordinary cyclic trigonometry, which is a special case in the limit κ → 0, such as:
- .
The κ-cyclic tangent and κ-cyclic cotangent functions are given by:
- .
The κ-cyclic trigonometric functions become the ordinary trigonometric function in the classical limit .
κ-Inverse cyclic function
The Kaniadakis inverse cyclic functions (or κ-inverse cyclic functions) are associated to the κ-logarithm:
- ,
- ,
- ,
- .
κ-Hyperbolic Trigonometry
The Kaniadakis hyperbolic trigonometry (or κ-hyperbolic trigonometry) is based on the κ-hyperbolic sine and κ-hyperbolic cosine given by:
- ,
- ,
where the κ-Euler formula is
- .
The κ-hyperbolic tangent and κ-hyperbolic cotangent functions are given by:
- .
The κ-hyperbolic trigonometric functions become the ordinary hyperbolic trigonometric functions in the classical limit .
From the κ-Euler formula and the property the fundamental expression of κ-hyperbolic trigonometry is given as follows:
κ-Inverse hyperbolic function
The Kaniadakis inverse hyperbolic functions (or κ-inverse hyperbolic functions) are associated to the κ-logarithm:
- ,
- ,
- ,
- ,
in which are valid the following relations:
- ,
- ,
- .
The κ-cyclic and κ-hyperbolic trigonometric functions are connected by the following relationships:
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- .
Kaniadakis entropy
The Kaniadakis statistics is based on the Kaniadakis κ-entropy, which is defined through:
where is a probability distribution function defined for a random variable , and is the entropic index.
The Kaniadakis κ-entropy is thermodynamically and Lesche stable[19][20] and obeys the Shannon-Khinchin axioms of continuity, maximality, generalized additivity and expandability.
Kaniadakis distributions
A Kaniadakis distribution (or κ-distribution) is a probability distribution derived from the maximization of Kaniadakis entropy under appropriate constraints. In this regard, several probability distributions emerge for analyzing a wide variety of phenomenology associated with experimental power-law tailed statistical distributions.
κ-Exponential distribution
κ-Gaussian distribution
κ-Gamma distribution
κ-Weibull distribution
κ-Logistic distribution
Kaniadakis integral transform
κ-Laplace Transform
The Kaniadakis Laplace transform (or κ-Laplace transform) is a κ-deformed integral transform of the ordinary Laplace transform. The κ-Laplace transform converts a function of a real variable to a new function in the complex frequency domain, represented by the complex variable . This κ-integral transform is defined as:[21]
The inverse κ-Laplace transform is given by:
The ordinary Laplace transform and its inverse transform are recovered as .
Properties
Let two functions and , and their respective κ-Laplace transforms and , the following table presents the main properties of κ-Laplace transform:[21]
| Property | ||
|---|---|---|
| Linearity | ||
| Time scaling | ||
| Frequency shifting | ||
| Derivative | ||
| Derivative | ||
| Time-domain integration | ||
| Dirac delta-function | ||
| Heaviside unit function | ||
| Power function | ||
| Power function | ||
| Power function |
The κ-Laplace transforms presented in the latter table reduce to the corresponding ordinary Laplace transforms in the classical limit .
κ-Fourier Transform
The Kaniadakis Fourier transform (or κ-Fourier transform) is a κ-deformed integral transform of the ordinary Fourier transform, which is consistent with the κ-algebra and the κ-calculus. The κ-Fourier transform is defined as:[22]
which can be rewritten as
where and . The κ-Fourier transform imposes an asymptotically log-periodic behavior by deforming the parameters and in addition to a damping factor, namely .

The kernel of the κ-Fourier transform is given by:
The inverse κ-Fourier transform is defined as:[22]
Let , the following table shows the κ-Fourier transforms of several notable functions:[22]
| Step function | ||
| Modulation | ||
| Causal -exponential | ||
| Symmetric -exponential | ||
| Constant | ||
| -Phasor | ||
| Impuslse | ||
| Signum | Sgn | |
| Rectangular |
The κ-deformed version of the Fourier transform preserves the main properties of the ordinary Fourier transform, as summarized in the following table.
| Linearity | |
| Scaling | where and |
| -Scaling | |
| Complex conjugation | |
| Duality | |
| Reverse | |
| -Frequency shift | |
| -Time shift | |
| Transform of -derivative | |
| -Derivative of transform | |
| Transform of integral | |
| -Convolution | where |
| Modulation |
The properties of the κ-Fourier transform presented in the latter table reduce to the corresponding ordinary Fourier transforms in the classical limit .
See also
References
- ↑ Kaniadakis, G. (2009). "Relativistic entropy and related Boltzmann kinetics". The European Physical Journal A. 40 (3): 275–287. arXiv:0901.1058. Bibcode:2009EPJA...40..275K. doi:10.1140/epja/i2009-10793-6. ISSN 1434-6001. S2CID 119190011.
- ↑ Kaniadakis, G. (2002). "Statistical mechanics in the context of special relativity". Physical Review E. 66 (5): 056125. arXiv:cond-mat/0210467. Bibcode:2002PhRvE..66e6125K. doi:10.1103/PhysRevE.66.056125. ISSN 1063-651X. PMID 12513574. S2CID 45635888.
- ↑ Kaniadakis, G. (2005). "Statistical mechanics in the context of special relativity. II". Physical Review E. 72 (3): 036108. arXiv:cond-mat/0507311. Bibcode:2005PhRvE..72c6108K. doi:10.1103/PhysRevE.72.036108. ISSN 1539-3755. PMID 16241516. S2CID 18115408.
- ↑ Kaniadakis, G. (2011). "Power-law tailed statistical distributions and Lorentz transformations". Physics Letters A. 375 (3): 356–359. arXiv:1110.3944. Bibcode:2011PhLA..375..356K. doi:10.1016/j.physleta.2010.11.057. ISSN 0375-9601. S2CID 118435479.
- ↑ Kaniadakis, G. (2001). "Non-linear kinetics underlying generalized statistics". Physica A: Statistical Mechanics and Its Applications. 296 (3): 405–425. arXiv:cond-mat/0103467. Bibcode:2001PhyA..296..405K. doi:10.1016/S0378-4371(01)00184-4. ISSN 0378-4371. S2CID 44275064.
- ↑ Kaniadakis, G. (2009). "Maximum entropy principle and power-law tailed distributions". The European Physical Journal B. 70 (1): 3–13. arXiv:0904.4180. Bibcode:2009EPJB...70....3K. doi:10.1140/epjb/e2009-00161-0. ISSN 1434-6028. S2CID 55421804.
- ↑ Kaniadakis, G. (2021). "New power-law tailed distributions emerging in κ-statistics (a)". Europhysics Letters. 133 (1): 10002. arXiv:2203.01743. Bibcode:2021EL....13310002K. doi:10.1209/0295-5075/133/10002. ISSN 0295-5075. S2CID 234144356.
- ↑ Carvalho, J. C.; Silva, R.; do Nascimento Jr., J. D.; De Medeiros, J. R. (2008). "Power law statistics and stellar rotational velocities in the Pleiades". EPL (Europhysics Letters). 84 (5): 59001. arXiv:0903.0836. Bibcode:2008EL.....8459001C. doi:10.1209/0295-5075/84/59001. ISSN 0295-5075. S2CID 7123391.
- ↑ Curé, Michel; Rial, Diego F.; Christen, Alejandra; Cassetti, Julia (2014). "A method to deconvolve stellar rotational velocities". Astronomy & Astrophysics. 565: A85. arXiv:1401.1054. Bibcode:2014A&A...565A..85C. doi:10.1051/0004-6361/201323344. ISSN 0004-6361. S2CID 59375612.
- ↑ Ourabah, Kamel; Hamici-Bendimerad, Amel Hiba; Tribeche, Mouloud (2015). "Quantum entanglement and Kaniadakis entropy". Physica Scripta. 90 (4): 045101. Bibcode:2015PhyS...90d5101O. doi:10.1088/0031-8949/90/4/045101. ISSN 0031-8949. S2CID 123776127.
- ↑ Abreu, Everton M. C.; Ananias Neto, Jorge; Mendes, Albert C. R.; de Paula, Rodrigo M. (2019). "Loop quantum gravity Immirzi parameter and the Kaniadakis statistics". Chaos, Solitons & Fractals. 118: 307–310. arXiv:1808.01891. Bibcode:2019CSF...118..307A. doi:10.1016/j.chaos.2018.11.033. ISSN 0960-0779. S2CID 119207713.
- ↑ Hristopulos, Dionissios T.; Petrakis, Manolis P.; Kaniadakis, Giorgio (2014). "Finite-size effects on return interval distributions for weakest-link-scaling systems". Physical Review E. 89 (5): 052142. arXiv:1308.1881. Bibcode:2014PhRvE..89e2142H. doi:10.1103/PhysRevE.89.052142. ISSN 1539-3755. PMID 25353774. S2CID 22310350.
- ↑ da Silva, Sérgio Luiz E. F. (2021). "κ-generalised Gutenberg–Richter law and the self-similarity of earthquakes". Chaos, Solitons & Fractals. 143: 110622. Bibcode:2021CSF...14310622D. doi:10.1016/j.chaos.2020.110622. ISSN 0960-0779. S2CID 234063959.
- ↑ Souza, N. T. C. M.; Anselmo, D. H. A. L.; Silva, R.; Vasconcelos, M. S.; Mello, V. D. (2014). "A κ -statistical analysis of the Y-chromosome". EPL (Europhysics Letters). 108 (3): 38004. doi:10.1209/0295-5075/108/38004. ISSN 0295-5075. S2CID 122456729.
- ↑ Costa, M. O.; Silva, R.; Anselmo, D. H. A. L.; Silva, J. R. P. (2019). "Analysis of human DNA through power-law statistics". Physical Review E. 99 (2): 022112. Bibcode:2019PhRvE..99b2112C. doi:10.1103/PhysRevE.99.022112. ISSN 2470-0045. PMID 30934358. S2CID 91186653.
- ↑ Clementi, Fabio; Gallegati, Mauro; Kaniadakis, Giorgio (2012). "A new model of income distribution: the κ-generalized distribution". Journal of Economics. 105 (1): 63–91. doi:10.1007/s00712-011-0221-0. hdl:11393/73598. ISSN 0931-8658. S2CID 155080665.
- ↑ Trivellato, Barbara (2013). "Deformed Exponentials and Applications to Finance". Entropy. 15 (12): 3471–3489. Bibcode:2013Entrp..15.3471T. doi:10.3390/e15093471. ISSN 1099-4300.
- ↑ Kaniadakis, Giorgio; Baldi, Mauro M.; Deisboeck, Thomas S.; Grisolia, Giulia; Hristopulos, Dionissios T.; Scarfone, Antonio M.; Sparavigna, Amelia; Wada, Tatsuaki; Lucia, Umberto (2020). "The κ-statistics approach to epidemiology". Scientific Reports. 10 (1): 19949. arXiv:2012.00629. Bibcode:2020NatSR..1019949K. doi:10.1038/s41598-020-76673-3. ISSN 2045-2322. PMC 7673996. PMID 33203913.
- ↑ Abe, S.; Kaniadakis, G.; Scarfone, A. M. (2004) [2004]. "Stabilities of generalized entropies". Journal of Physics A: Mathematical and General. 37 (44): 10513–10519. arXiv:cond-mat/0401290. Bibcode:2004JPhA...3710513A. doi:10.1088/0305-4470/37/44/004. S2CID 16080176.
- ↑ Kaniadakis, G. (2001). "H-theorem and generalized entropies within the framework of nonlinear kinetics". Physics Letters A. 288 (5–6): 283–291. arXiv:cond-mat/0109192. Bibcode:2001PhLA..288..283K. doi:10.1016/S0375-9601(01)00543-6. S2CID 119445915.
- 1 2 Kaniadakis, Giorgio (2013-09-25). "Theoretical Foundations and Mathematical Formalism of the Power-Law Tailed Statistical Distributions". Entropy. 15 (12): 3983–4010. arXiv:1309.6536. Bibcode:2013Entrp..15.3983K. doi:10.3390/e15103983. ISSN 1099-4300.
- 1 2 3 Scarfone, A.M. (2017). "κ -deformed Fourier transform". Physica A: Statistical Mechanics and Its Applications. 480: 63–78. arXiv:2206.06869. Bibcode:2017PhyA..480...63S. doi:10.1016/j.physa.2017.03.036. S2CID 126079408.