Example of Kautz graph on 3 characters with string length 2 (on the left) and 3 (on the right); the edges on the left correspond to the vertices on the right.

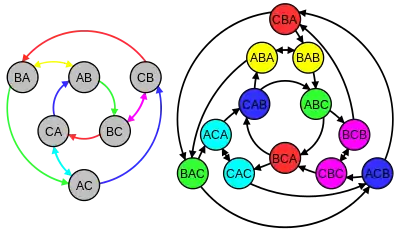
The Kautz graph ${\displaystyle K_{M}^{N+1}}$ is a directed graph of degree ${\displaystyle M}$ and dimension ${\displaystyle N+1}$, which has ${\displaystyle (M+1)M^{N}}$ vertices labeled by all possible strings ${\displaystyle s_{0}\cdots s_{N}}$ of length ${\displaystyle N+1}$ which are composed of characters ${\displaystyle s_{i}}$ chosen from an alphabet ${\displaystyle A}$ containing ${\displaystyle M+1}$ distinct symbols, subject to the condition that adjacent characters in the string cannot be equal (${\displaystyle s_{i}\neq s_{i+1}}$).

The Kautz graph ${\displaystyle K_{M}^{N+1}}$ has ${\displaystyle (M+1)M^{N+1}}$ edges

${\displaystyle \{(s_{0}s_{1}\cdots s_{N},s_{1}s_{2}\cdots s_{N}s_{N+1})|\;s_{i}\in A\;s_{i}\neq s_{i+1}\}\,}$

It is natural to label each such edge of ${\displaystyle K_{M}^{N+1}}$ as ${\displaystyle s_{0}s_{1}\cdots s_{N+1}}$, giving a one-to-one correspondence between edges of the Kautz graph ${\displaystyle K_{M}^{N+1}}$ and vertices of the Kautz graph ${\displaystyle K_{M}^{N+2}}$.

Kautz graphs are closely related to De Bruijn graphs.

Properties

• For a fixed degree ${\displaystyle M}$ and number of vertices ${\displaystyle V=(M+1)M^{N}}$, the Kautz graph has the smallest diameter of any possible directed graph with ${\displaystyle V}$ vertices and degree ${\displaystyle M}$.
• All Kautz graphs have Eulerian cycles. (An Eulerian cycle is one which visits each edge exactly once—This result follows because Kautz graphs have in-degree equal to out-degree for each node)
• All Kautz graphs have a Hamiltonian cycle (This result follows from the correspondence described above between edges of the Kautz graph ${\displaystyle K_{M}^{N}}$ and vertices of the Kautz graph ${\displaystyle K_{M}^{N+1}}$; a Hamiltonian cycle on ${\displaystyle K_{M}^{N+1}}$ is given by an Eulerian cycle on ${\displaystyle K_{M}^{N}}$)
• A degree-${\displaystyle k}$ Kautz graph has ${\displaystyle k}$ disjoint paths from any node ${\displaystyle x}$ to any other node ${\displaystyle y}$.

In computing

The Kautz graph has been used as a network topology for connecting processors in high-performance computing^[1] and fault-tolerant computing^[2] applications: such a network is known as a Kautz network.

Notes

This article incorporates material from Kautz graph on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.