The Koutecký–Levich equation models the measured electric current at an electrode from an electrochemical reaction in relation to the kinetic activity and the mass transport of reactants.

A visualization of the Koutecký–Levich equation. The graph shows the measured current as a function of the mass transport current for given kinetic current.

The Koutecký–Levich equation can be written as^[1]:

${\displaystyle {1 \over i_{m}}={1 \over i_{K}}+{1 \over i_{MT}}}$

where

• i_m is the measured current (A).
• i_K is the kinetic current (A) from the electrochemical reactions.
• i_MT is the mass transport current (A).

Note the similarity of this equation to the conductance of an electrical circuits in parallel.

The Koutecký–Levich equation is also commonly expressed as:

${\displaystyle i_{m}={i_{K}i_{MT} \over i_{K}+i_{MT}}}$

The kinetic current (i_K) can be modeled by the Butler-Volmer Equation and is characterized by being potential dependent. On the other hand, the mass transport current (i_MT) depends on the particular electrochemical setup and amount of stirring.

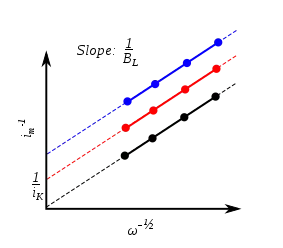
Koutecký–Levich plot

In the case a rotating disk electrode setup is used and the electrode is flat and smooth, the i_MT can modeled using the Levich equation.^[1][2] Inserted in the Koutecký–Levich equation, we get:

Koutecký-Levich Plot. The inverse measured current is plotted versus the inverse square root of rotation rate

${\displaystyle {1 \over i_{m}}={1 \over i_{K}}+{1 \over {B_{L}\omega ^{0.5}}}}$

where:

• B_L is the Levich Constant.
• ω is the angular rotation rate of the electrode (rad/s)

From an experimental data set where the current is measured at different rotation rates, it is possible to extract the kinetic current from a so-called Koutecký–Levich plot. In a Koutecký–Levich plot the inverse measured current is plotted versus the inverse square root of the rotation rate. This will linearize the data set and the inverse of the kinetic current can be obtained by extrapolating the line to the ordinate. This y-intercept corresponds to taking the rotation rate up to infinity, where the reaction is not mass-transport limited. Koutecký–Levich analysis is therefore used to determine the kinetic constants of the reaction such as the kinetic constant ${\displaystyle k^{o}}$ and the symmetry factor ${\displaystyle \alpha }$.

References