LEA (cipher)

LEA
	LEA encryption round function
General
Designers	Deukjo Hong, Jung-Keun Lee, Dong-Chan Kim, Daesung Kwon, Kwon Ho Ryu, Dong-Geon Lee
First published	2013
Cipher detail
Key sizes	128, 192, or 256 bits
Block sizes	128 bits
Structure	ARX (modular Addition, bitwise Rotation, and bitwise XOR)
Rounds	24, 28, or 32 (depending on key size)
Best public cryptanalysis
	As of 2019, no successful attack on full-round LEA is known.

The Lightweight Encryption Algorithm (also known as LEA) is a 128-bit block cipher developed by South Korea in 2013 to provide confidentiality in high-speed environments such as big data and cloud computing, as well as lightweight environments such as IoT devices and mobile devices.^[1] LEA has three different key lengths: 128, 192, and 256 bits. LEA encrypts data about 1.5 to 2 times faster than AES, the most widely used block cipher in various software environments.

LEA is one of the cryptographic algorithms approved by the Korean Cryptographic Module Validation Program (KCMVP) and is the national standard of Republic of Korea (KS X 3246). LEA is included in the ISO/IEC 29192-2:2019 standard (Information security - Lightweight cryptography - Part 2: Block ciphers).

Specification

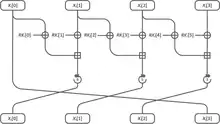
The block cipher LEA consisting of ARX operations (modular Addition: $\boxplus$ , bitwise Rotation: $\lll$ , $\ggg$ , and bitwise XOR $\oplus$ ) for 32-bit words processes data blocks of 128 bits and has three different key lengths: 128, 192, and 256 bits. LEA with a 128-bit key, LEA with a 192-bit key, and LEA with a 256-bit key are referred to as “LEA-128”, “LEA-192”, and “LEA-256”, respectively. The number of rounds is 24 for LEA-128, 28 for LEA-192, and 32 for LEA-256.

Encryption

Let $P=P[0]\|P[1]\|P[2]\|P[3]$ be a 128-bit block of plaintext and $C=C[0]\|C[1]\|C[2]\|C[3]$ be a 128-bit block of ciphertext, where $P[i]$ and $C[i]$ ( $0\leq i<4$ ) are 32-bit blocks. Let $K_{i}=K_{i}[0]\|K_{i}[1]\|K_{i}[2]\|K_{i}[3]\|K_{i}[4]\|K_{i}[5]$ ( $0\leq i<Nr$ ) be 192-bit round keys, where $K_{i}[j]$ ( $0\leq j<6$ ) are 32-bit blocks. Here $Nr$ is the number of rounds for the LEA algorithm. The encryption operation is described as follows:

$X_{0}[0]\|X_{0}[1]\|X_{0}[2]\|X_{0}[3]\leftarrow P[0]\|P[1]\|P[2]\|P[3]$
for $i=0$ $i=0$ to $Nr-1$ $Nr-1$
1. $X_{i+1}[0]\leftarrow \left(\left(X_{i}[0]\oplus K_{i}[0]\right)\boxplus \left(X_{i}[1]\oplus K_{i}[1]\right)\right)\lll 9$
2. $X_{i+1}[1]\leftarrow \left(\left(X_{i}[1]\oplus K_{i}[2]\right)\boxplus \left(X_{i}[2]\oplus K_{i}[3]\right)\right)\ggg 5$
3. $X_{i+1}[2]\leftarrow \left(\left(X_{i}[2]\oplus K_{i}[4]\right)\boxplus \left(X_{i}[3]\oplus K_{i}[5]\right)\right)\ggg 3$
4. $X_{i+1}[3]\leftarrow X_{i}[0]$
$C[0]\|C[1]\|C[2]\|C[3]\leftarrow X_{Nr}[0]\|X_{Nr}[1]\|X_{Nr}[2]\|X_{Nr}[3]$

Decryption

The decryption operation is as follows:

$X_{Nr}[0]\|X_{Nr}[1]\|X_{Nr}[2]\|X_{Nr}[3]\leftarrow C[0]\|C[1]\|C[2]\|C[3]$
for $i=(Nr-1)$ $i=(Nr-1)$ down to $0$ $0$
1. $X_{i}[0]\leftarrow X_{i+1}[3]$
2. $X_{i}[1]\leftarrow \left(\left(X_{i+1}[0]\ggg 9\right)\boxminus \left(X_{i}[0]\oplus K_{i}[0]\right)\right)\oplus K_{i}[1]$
3. $X_{i}[2]\leftarrow \left(\left(X_{i+1}[1]\lll 5\right)\boxminus \left(X_{i}[1]\oplus K_{i}[2]\right)\right)\oplus K_{i}[3]$
4. $X_{i}[3]\leftarrow \left(\left(X_{i+1}[2]\lll 3\right)\boxminus \left(X_{i}[2]\oplus K_{i}[4]\right)\right)\oplus K_{i}[5]$
$P[0]\|P[1]\|P[2]\|P[3]\leftarrow X_{0}[0]\|X_{0}[1]\|X_{0}[2]\|X_{0}[3]$

Key schedule

The key schedule of LEA supports 128, 192, and 256-bit keys and outputs 192-bit round keys $K_{i}$ ( $0\leq i<Nr$ ) for the data processing part.

Key schedule for LEA-128

Let $K=K[0]\|K[1]\|K[2]\|K[3]$ be a 128-bit key, where $K[i]$ ( $0\leq i<4$ ) are 32-bit blocks. The key schedule for LEA-128 takes $K$ and four 32-bit constants $\delta [i]$ ( $0\leq i<4$ ) as inputs and outputs twenty-four 192-bit round keys $K_{i}$ ( $0\leq i<24$ ). The key schedule operation for LEA-128 is as follows:

$T[0]\|T[1]\|T[2]\|T[3]\leftarrow K[0]\|K[1]\|K[2]\|K[3]$
for $i=0$ $i=0$ to $23$ $23$
1. $T[0]\leftarrow \left(T[0]\boxplus \left(\delta [i\mod 4]\lll i\right)\right)\lll 1$
2. $T[1]\leftarrow \left(T[1]\boxplus \left(\delta [i\mod 4]\lll \left(i+1\right)\right)\right)\lll 3$
3. $T[2]\leftarrow \left(T[2]\boxplus \left(\delta [i\mod 4]\lll \left(i+2\right)\right)\right)\lll 6$
4. $T[3]\leftarrow \left(T[3]\boxplus \left(\delta [i\mod 4]\lll \left(i+3\right)\right)\right)\lll 11$
5. $K_{i}\leftarrow T[0]\|T[1]\|T[2]\|T[1]\|T[3]\|T[1]$

Key schedule for LEA-192

Let $K=K[0]\|K[1]\|K[2]\|K[3]\|K[4]\|K[5]$ be a 192-bit key, where $K[i]$ ( $0\leq i<6$ ) are 32-bit blocks. The key schedule for LEA-192 takes $K$ and six 32-bit constants $\delta [i]$ ( $0\leq i<6$ ) as inputs and outputs twenty-eight 192-bit round keys $K_{i}$ ( $0\leq i<28$ ). The key schedule operation for LEA-192 is as follows:

$T[0]\|T[1]\|T[2]\|T[3]\|T[4]\|T[5]\leftarrow K[0]\|K[1]\|K[2]\|K[3]\|K[4]\|K[5]$
for $i=0$ $i=0$ to $27$ $27$
1. $T[0]\leftarrow \left(T[0]\boxplus \left(\delta [i\mod 6]\lll i\right)\right)\lll 1$
2. $T[1]\leftarrow \left(T[1]\boxplus \left(\delta [i\mod 6]\lll \left(i+1\right)\right)\right)\lll 3$
3. $T[2]\leftarrow \left(T[2]\boxplus \left(\delta [i\mod 6]\lll \left(i+2\right)\right)\right)\lll 6$
4. $T[3]\leftarrow \left(T[3]\boxplus \left(\delta [i\mod 6]\lll \left(i+3\right)\right)\right)\lll 11$
5. $T[4]\leftarrow \left(T[4]\boxplus \left(\delta [i\mod 6]\lll \left(i+4\right)\right)\right)\lll 13$
6. $T[5]\leftarrow \left(T[5]\boxplus \left(\delta [i\mod 6]\lll \left(i+5\right)\right)\right)\lll 17$
7. $K_{i}\leftarrow T[0]\|T[1]\|T[2]\|T[3]\|T[4]\|T[5]$

Key schedule for LEA-256

Let $K=K[0]\|K[1]\|K[2]\|K[3]\|K[4]\|K[5]\|K[6]\|K[7]$ be a 256-bit key, where $K[i]$ ( $0\leq i<8$ ) are 32-bit blocks. The key schedule for LEA-192 takes $K$ and eight 32-bit constants $\delta [i]$ ( $0\leq i<8$ ) as inputs and outputs thirty-two 192-bit round keys $K_{i}$ ( $0\leq i<32$ ). The key schedule operation for LEA-256 is as follows:

$T[0]\|T[1]\|T[2]\|T[3]\|T[4]\|T[5]\|T[6]\|T[7]\leftarrow K[0]\|K[1]\|K[2]\|K[3]\|K[4]\|K[5]\|K[6]\|K[7]$
for $i=0$ $i=0$ to $31$ $31$
1. $T[6i\mod 8]\leftarrow \left(T[6i\mod 8]\boxplus \left(\delta [i\mod 8]\lll i\right)\right)\lll 1$
2. $T[6i+1\mod 8]\leftarrow \left(T[6i+1\mod 8]\boxplus \left(\delta [i\mod 8]\lll \left(i+1\right)\right)\right)\lll 3$
3. $T[6i+2\mod 8]\leftarrow \left(T[6i+2\mod 8]\boxplus \left(\delta [i\mod 8]\lll \left(i+2\right)\right)\right)\lll 6$
4. $T[6i+3\mod 8]\leftarrow \left(T[6i+3\mod 8]\boxplus \left(\delta [i\mod 8]\lll \left(i+3\right)\right)\right)\lll 11$
5. $T[6i+4\mod 8]\leftarrow \left(T[6i+4\mod 8]\boxplus \left(\delta [i\mod 8]\lll \left(i+4\right)\right)\right)\lll 13$
6. $T[6i+5\mod 8]\leftarrow \left(T[6i+5\mod 8]\boxplus \left(\delta [i\mod 8]\lll \left(i+5\right)\right)\right)\lll 17$
7. $K_{i}\leftarrow T[6i\mod 8]\|T[6i+1\mod 8]\|T[6i+2\mod 8]\|T[6i+3\mod 8]\|T[6i+4\mod 8]\|T[6i+5\mod 8]$

Constant values

The eight 32-bit constant values $\delta [i]$ ( $0\leq i<8$ ) used in the key schedule are given in the following table.

Constant values used in the key schedule
$i$	0	1	2	3	4	5	6	7
$\delta [i]$	0xc3efe9db	0x44626b02	0x79e27c8a	0x78df30ec	0x715ea49e	0xc785da0a	0xe04ef22a	0xe5c40957

Security

As of 2019, no successful attack on full-round LEA is known. As is typical for iterated block ciphers, reduced-round variants have been attacked. The best published attacks on LEA in the standard attack model (CPA/CCA with unknown key) are boomerang attacks and differential linear attacks. The security margin to the whole rounds ratio is greater than 37% against various existing cryptanalytic techniques for block ciphers.

Security of LEA-128 (24 rounds)
Attack type	Attacked rounds
Differential^[2]	14
Truncated differential^[2]	14
Linear^[1]	13
Zero correlation^[1]	10
Boomerang^[1]	15
Impossible differential^[1]	12
Integral^[1]	9
Differential linear^[1]	15
Related-key differential^[1]	13

Security margins of LEA
Block ciphers	Rounds (Attacked / Total)	Security margins
LEA-128	15 / 24	37.50%
LEA-192	16 / 28	42.85%
LEA-256	18 / 32	43.75%

Performance

LEA has very good performance in a general-purpose software environment. In particular, it is possible to encrypt at a rate of about 1.5 to 2 times on average, compared to AES, the most widely used block cipher in various software environments. The tables below compare the performance of LEA and AES using FELICS (Fair Evaluation of Lightweight Cryptographic Systems),^[3] a benchmarking framework for evaluation of software implementations of lightweight cryptographic primitives.

FELICS scenario 1 – Enc. + Dec. + KeySetup / 128-byte CBC-Encryption^[4] (Code: bytes, RAM: bytes, Time: cycles)
Platform		LEA-128	LEA-192	LEA-256	AES-128
AVR	Code	1,684	2,010	2,150	3,010
	RAM	631	943	1,055	408
	Time	61,020	80,954	92,194	58,248
MSP	Code	1,130	1,384	1,468	2,684
	RAM	626	942	1,046	408
	Time	47,339	56,540	64,001	86,506
ARM	Code	472	536	674	3,050
	RAM	684	968	1,080	452
	Time	17,417	20,640	24,293	83,868

FELICS scenario 2 – Enc. / 128-bit CTR-Encryption^[4] (Code: bytes, RAM: bytes, Time: cycles)
Platform		LEA-128	LEA-192	LEA-256	AES-128
AVR	Code	906	1,210	1,306	1,246
	RAM	80	80	80	81
	Time	4,023	4,630	5,214	3,408
MSP	Code	722	1,014	1,110	1,170
	RAM	78	78	78	80
	Time	2,814	3,242	3,622	4,497
ARM	Code	628	916	1,012	1,348
	RAM	92	100	100	124
	Time	906	1,108	1,210	4,044

Test vectors

Test vectors for LEA for each key length are as follows.^[5] All values are expressed in hexadecimal form.

LEA-128
- Key: 0f 1e 2d 3c 4b 5a 69 78 87 96 a5 b4 c3 d2 e1 f0
- Plaintext: 10 11 12 13 14 15 16 17 18 19 1a 1b 1c 1d 1e 1f
- Ciphertext: 9f c8 4e 35 28 c6 c6 18 55 32 c7 a7 04 64 8b fd
LEA-192
- Key: 0f 1e 2d 3c 4b 5a 69 78 87 96 a5 b4 c3 d2 e1 f0 f0 e1 d2 c3 b4 a5 96 87
- Plaintext: 20 21 22 23 24 25 26 27 28 29 2a 2b 2c 2d 2e 2f
- Ciphertext: 6f b9 5e 32 5a ad 1b 87 8c dc f5 35 76 74 c6 f2
LEA-256
- Key: 0f 1e 2d 3c 4b 5a 69 78 87 96 a5 b4 c3 d2 e1 f0 f0 e1 d2 c3 b4 a5 96 87 78 69 5a 4b 3c 2d 1e 0f
- Plaintext: 30 31 32 33 34 35 36 37 38 39 3a 3b 3c 3d 3e 3f
- Ciphertext: d6 51 af f6 47 b1 89 c1 3a 89 00 ca 27 f9 e1 97

Implementations

LEA is free for any use: public or private, commercial or non-commercial. The source code for distribution of LEA implemented in C, Java, and Python can be downloaded from KISA's website.^[6] In addition, LEA is contained in Crypto++ library, a free C++ class library of cryptographic schemes.^[7]

KCMVP

LEA is one of the cryptographic algorithms approved by the Korean Cryptographic Module Validation Program (KCMVP).^[8]

Standardization

LEA is included in the following standards.

KS X 3246, 128-bit block cipher LEA (in Korean)^[5]

ISO/IEC 29192-2:2019, Information security - Lightweight cryptography - Part 2: Block ciphers^[9]

References

1 2 3 4 5 6 7 8 Hong, Deukjo; Lee, Jung-Keun; Kim, Dong-Chan; Kwon, Daesung; Ryu, Kwon Ho; Lee, Dong-Geon (2014). "LEA: A 128-Bit Block Cipher for Fast Encryption on Common Processors". Information Security Applications. Lecture Notes in Computer Science. Vol. 8267. Springer International Publishing. pp. 3–27. doi:10.1007/978-3-319-05149-9_1. ISBN 978-3-319-05149-9.
1 2 Song, Ling; Huang, Zhangjie; Yang, Qianqian (2016). "Automatic Differential Analysis of ARX Block Ciphers with Application to SPECK and LEA". Information Security and Privacy. Lecture Notes in Computer Science. Vol. 9723. Springer International Publishing. pp. 379–394. doi:10.1007/978-3-319-40367-0_24. ISBN 978-3-319-40367-0.
↑ Dinu, Daniel; Corre, Yann Le; Khovratovich, Dmitry; Perrin, Léo; Großschädl, Johann; Biryukov, Alex (14 July 2018). "Triathlon of lightweight block ciphers for the Internet of things" (PDF). Journal of Cryptographic Engineering. 9 (3): 283–302. doi:10.1007/s13389-018-0193-x. S2CID 1578215.
1 2 "CryptoLUX > FELICS". cryptolux.org.
1 2 "KS X 3246, 128-bit block cipher LEA (in Korean)".
↑ "KISA 암호이용활성화 - 암호알고리즘 소스코드". seed.kisa.or.kr.
↑ "Crypto++ Library 8.2 | Free C++ Class Library of Cryptographic Schemes". www.cryptopp.com.
↑ "KISA 암호이용활성화 - 개요". seed.kisa.or.kr.
↑ "ISO/IEC 29192-2:2019, Information security - Lightweight cryptography - Part 2: Block ciphers".

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[HLK+13-1] 1 2 3 4 5 6 7 8 Hong, Deukjo; Lee, Jung-Keun; Kim, Dong-Chan; Kwon, Daesung; Ryu, Kwon Ho; Lee, Dong-Geon (2014). "LEA: A 128-Bit Block Cipher for Fast Encryption on Common Processors". Information Security Applications. Lecture Notes in Computer Science. Vol. 8267. Springer International Publishing. pp. 3–27. doi:10.1007/978-3-319-05149-9_1. ISBN 978-3-319-05149-9.

[SHY16-2] 1 2 Song, Ling; Huang, Zhangjie; Yang, Qianqian (2016). "Automatic Differential Analysis of ARX Block Ciphers with Application to SPECK and LEA". Information Security and Privacy. Lecture Notes in Computer Science. Vol. 9723. Springer International Publishing. pp. 379–394. doi:10.1007/978-3-319-40367-0_24. ISBN 978-3-319-40367-0.

[FELICS-3] Dinu, Daniel; Corre, Yann Le; Khovratovich, Dmitry; Perrin, Léo; Großschädl, Johann; Biryukov, Alex (14 July 2018). "Triathlon of lightweight block ciphers for the Internet of things" (PDF). Journal of Cryptographic Engineering. 9 (3): 283–302. doi:10.1007/s13389-018-0193-x. S2CID 1578215.

[FELICS_web-4] 1 2 "CryptoLUX > FELICS". cryptolux.org.

[KS_X_3246-5] 1 2 "KS X 3246, 128-bit block cipher LEA (in Korean)".

[LEA_source-6] "KISA 암호이용활성화 - 암호알고리즘 소스코드". seed.kisa.or.kr.

[LEA_cryptopp-7] "Crypto++ Library 8.2 | Free C++ Class Library of Cryptographic Schemes". www.cryptopp.com.

[KCMVP-8] "KISA 암호이용활성화 - 개요". seed.kisa.or.kr.

[ISO_IEC_29192-2-9] "ISO/IEC 29192-2:2019, Information security - Lightweight cryptography - Part 2: Block ciphers".

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]