Landau kernel

The Landau kernel is named after the German number theorist Edmund Landau. The kernel is a summability kernel defined as:^[1]

L_{n}(t)={\begin{cases}{\frac {(1-t^{2})^{n}}{c_{n}}}&{\text{if }}-1\leq t\leq 1\\0&{\text{otherwise}}\end{cases}}

where the coefficients $c_{n}$ are defined as follows

c_{n}=\int _{-1}^{1}(1-t^{2})^{n}\,dt

Visualisation

In these plotted functions,

L 10 (t)

represent the blue,

L 50 (t)

represent the green,

L 100 (t)

represent the turquoise, and

L 200 (t)

represent the purple curve.

Using integration by parts, one can show that:^[2]

c_{n}={\frac {(n!)^{2}\,2^{2n+1}}{(2n)!(2n+1)}}.

Hence, this implies that the Landau Kernel can be defined as follows:

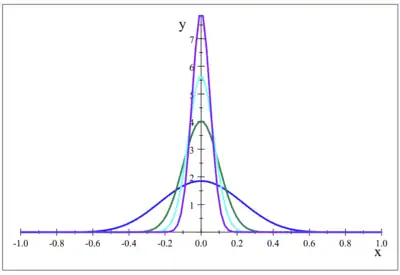
L_{n}(t)={\begin{cases}(1-t^{2})^{n}{\frac {(2n)!(2n+1)}{(n!)^{2}\,2^{2n+1}}}&{\text{for t}}\in [-1,1]\\0&{\text{elsewhere}}\end{cases}}

Plotting this function for different values of n reveals that as n goes to infinity, $L_{n}(t)$ approaches the Dirac delta function, as seen in the image,^[1] where the following functions are plotted.

Properties

Some general properties of the Landau kernel is that it is nonnegative and continuous on $\mathbb {R}$ . These properties are made more concrete in the following section.

Dirac sequences

Definition: Dirac Sequence — A Dirac Sequence is a sequence { $K_{n}(t)$ } of functions $K_{n}(t)\colon \mathbb {R} \to \mathbb {R}$ that satisfies the following properities:

$K_{n}(t)\geq 0,\,\,\forall t\in \mathbb {R} {\text{ and }}\forall n\in \mathbb {Z}$
$\int _{-\infty }^{\infty }K_{n}(t)\,dt=1,\,\forall n$
$\forall \epsilon >0,\,\forall \delta >0,\,\exists N\in \mathbb {Z} _{+}{\text{ such that }}\forall n\geq N:\int _{\mathbb {R} \setminus [-\delta ,\delta ]}K_{n}(t)\,dt=\int _{-\infty }^{-\delta }K_{n}(t)\,dt+\int _{\delta }^{\infty }K_{n}(t)\,dt<\epsilon$

The third bullet point means that the area under the graph of the function $y=K_{n}(t)$ becomes increasingly concentrated close to the origin as n approaches infinity. This definition lends us to the following theorem.

Theorem — The sequence of Landau Kernels is a Dirac sequence

Proof: We prove the third property only. In order to do so, we introduce the following lemma:

Lemma — The coefficients satsify the following relationship, $c_{n}\geq {\frac {2}{n+1}}$

Proof of the Lemma:

Using the definition of the coefficients above, we find that the integrand is even, we may write

{\frac {c_{n}}{2}}=\int _{0}^{1}(1-t^{2})^{n}\,dt=\int _{0}^{1}(1-t)^{n}(1+t)^{n}\,dt\geq \int _{0}^{1}(1-t)^{n}\,dt={\frac {1}{1+n}}

completing the proof of the lemma. A corollary of this lemma is the following:

Corollary — For all positive, real ${\displaystyle \delta$ $\int _{\mathbb {R} \setminus [-\delta ,\delta ]}K_{n}(t)\,dt\leq {\frac {2}{c_{n}}}\int _{\delta }^{1}(1-t^{2})^{n}\,dt\leq (n+1)(1-r^{2})^{n}$

References

1 2 Terras, Audrey (May 25, 2009). "Lecture 8. Dirac and Weierstrass" (PDF).
↑ Hilber, Courant. Methods of Mathematical Physics, Vol. I. p. 84.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[:0-1] 1 2 Terras, Audrey (May 25, 2009). "Lecture 8. Dirac and Weierstrass" (PDF).

[2] Hilber, Courant. Methods of Mathematical Physics, Vol. I. p. 84.

[1]

[2]

Visualisation

Properties

Dirac sequences

See also

References