Laboratory quality control is designed to detect, reduce, and correct deficiencies in a laboratory's internal analytical process prior to the release of patient results, in order to improve the quality of the results reported by the laboratory. Quality control (QC) is a measure of precision, or how well the measurement system reproduces the same result over time and under varying operating conditions. Laboratory quality control material is usually run at the beginning of each shift, after an instrument is serviced, when reagent lots are changed, after equipment calibration, and whenever patient results seem inappropriate.[1] Quality control material should approximate the same matrix as patient specimens, taking into account properties such as viscosity, turbidity, composition, and color. It should be simple to use, with minimal vial-to-vial variability, because variability could be misinterpreted as systematic error in the method or instrument. It should be stable for long periods of time, and available in large enough quantities for a single batch to last at least one year. Liquid controls are more convenient than lyophilized (freeze-dried) controls because they do not have to be reconstituted, minimizing pipetting error. Dried Tube Specimen (DTS) is slightly cumbersome as a QC material but it is very low-cost, stable over long periods and efficient, especially useful for resource-restricted settings in under-developed and developing countries.[2] DTS can be manufactured[3] in-house by a laboratory or Blood Bank for its use.

Interpretation

Interpretation of quality control data involves both graphical and statistical methods. Quality control data is most easily visualized using a Levey–Jennings chart. The dates of analyses are plotted along the x-axis and control values are plotted along the y-axis. The pattern of plotted points provides a simple way to detect increased random error and shifts or trends in calibration.[4]

The control charts

Control charts are a statistical approach to the study of manufacturing process variation for the purpose of improving the economic effectiveness of the process. These methods are based on continuous monitoring of process variation. The control chart, also known as the Shewhart chart or process-behavior chart, is a statistical tool intended to assess the nature of variation in a process and to facilitate forecasting and management. A control chart is a more specific kind of run chart. The control chart is one of the seven basic tools of quality control, which also include the histogram, pareto chart, check sheet, cause and effect diagram, flowchart and scatter diagram. Control charts prevent unnecessary process adjustments, provide information about process capability, provide diagnostic information, and are a proven technique for improving productivity.

Levey–Jennings chart

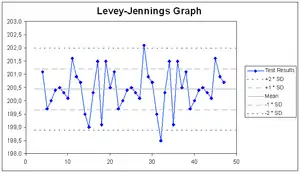
An example of a Levey–Jennings chart with upper and lower limits of one and two times the standard deviation

A Levey–Jennings chart is a graph that quality control data is plotted on to give a visual indication whether a laboratory test is working well. The distance from the mean is measured in standard deviations. It is named after Stanley Levey and E. R. Jennings, pathologists who suggested in 1950 that Shewhart's individuals control chart could be used in the clinical laboratory.[5] The date and time, or more often the number of the control run, is plotted on the x-axis. A mark is made indicating how far the actual result was from the mean, which is the expected value for the control. Lines run across the graph at the mean, as well as one, two and three standard deviations to either side of the mean. This makes it easy to see how far off the result was.

Rules such as the Westgard rules can be applied to see whether the results from the samples when the control was done can be released, or if they need to be rerun. The formulation of Westgard rules were based on statistical methods. Westgard rules are commonly used to analyse data in Shewhart control charts. Westgard rules are used to define specific performance limits for a particular assay (test) and can be used to detect both random and systematic errors. Westgard rules are programmed into automated analyzers to determine when an analytical run should be rejected. These rules need to be applied carefully so that true errors are detected while false rejections (of valid results that are outside of range) are minimized. The rules applied to high-volume chemistry and hematology instruments should produce low false rejection rates.[6][7]

The Levey–Jennings chart differs from the Shewhart individuals control chart because the standard deviation (σ, "sigma") is estimated. The Levey–Jennings chart uses the long-term (i.e., population) estimate of sigma whereas the Shewhart chart uses the short-term (i.e., within the rational subgroup) estimate.

Validation and verification

Validation and verification of medical devices ensure that they fulfil their intended purpose. Validation or verification is generally needed when a health facility acquires a new device to perform medical tests.

The main difference between the two is that validation is focused on ensuring that the device meets the needs and requirements of its intended users and the intended use environment, whereas verification is focused on ensuring that the device meets its specified design requirements.

Analytical sensitivity and specificity

"Analytical sensitivity" is defined as the smallest amount of substance in a sample that can accurately be measured by an assay (synonymously to detection limit), and "analytical specificity" is defined as the ability of an assay to measure one particular organism or substance, rather than others.[8] These definitions are different from diagnostic sensitivity and diagnostic specificity, which are measures of how well a test can identify true positives and true negatives, respectively.

See also

References

  1. ↑ Tietz, N.W. (1987). "Fundamentals of Clinical Chemistry", Third Edition, W.B. Saunder Company.
  2. ↑ Dhoot, Ashish; Mammen, Joy; Mathews, Nitty; Kannangai, Rajesh; Daniel, Dolly; S, Prasannakumar (2022-06-04). "Internal quality control for HIV testing of blood donors - Dried tube specimen as a cost-effective alternative". Asian Journal of Transfusion Science. 16 (2): 234. doi:10.4103/ajts.ajts_75_21. eISSN 1998-3565. PMC 9855207. PMID 36687551. S2CID 249252889. Retrieved August 5, 2022.
  3. ↑ Parekh, Bharat S.; Anyanwu, Juliana; Patel, Hetal; Downer, Marie; Kalou, Mireille; Gichimu, Catherine; Keipkerich, Bera Steven; Clement, Nelly; Omondi, Michael; Mayer, Oren; Ou, Chin-Yih (2010-02-01). "Dried tube specimens: A simple and cost-effective method for preparation of HIV proficiency testing panels and quality control materials for use in resource-limited settings". Journal of Virological Methods. 163 (2): 295–300. doi:10.1016/j.jviromet.2009.10.013. ISSN 0166-0934. PMID 19878697.
  4. ↑ Grant, E. L. and R. S. Leavenworth (1988). "Statistical Quality Control", Sixth Edition, McGraw-Hill Book Company.
  5. ↑ Levey, Stanley; Jennings, E. R. (November 1, 1950). "The use of Control Charts in the Clinical Laboratory". American Journal of Clinical Pathology. 20 (11): 1059–1066. doi:10.1093/ajcp/20.11_ts.1059. PMID 14783086 – via Oxford Academic.
  6. ↑ Westgard, J. O., P. L. Barry (1986). "Cost-Effective Quality Control: Managing the Quality and Productivity of Analytical Processes", AACC Press.
  7. ↑ Westgard, J. O., P. L. Barry, and M. R. Hunt (1981). "A Multi-rule Shewhart Chart for Quality Control in Clinical Chemistry", Clinical Chemistry, vol. 27, pp. 493–501.
  8. ↑ Saah AJ, Hoover DR (1998). "[Sensitivity and specificity revisited: significance of the terms in analytic and diagnostic language]". Ann Dermatol Venereol. 125 (4): 291–4. PMID 9747274.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.