| Computing devices in |
| Rabdology |
|---|
| Napier's bones |
| Promptuary |
| Location arithmetic |
Location arithmetic (Latin arithmeticae localis) is the additive (non-positional) binary numeral systems, which John Napier explored as a computation technique in his treatise Rabdology (1617), both symbolically and on a chessboard-like grid.
Napier's terminology, derived from using the positions of counters on the board to represent numbers, is potentially misleading because the numbering system is, in facts, non-positional in current vocabulary.
During Napier's time, most of the computations were made on boards with tally-marks or jetons. So, unlike how it may be seen by the modern reader, his goal was not to use moves of counters on a board to multiply, divide and find square roots, but rather to find a way to compute symbolically with pen and paper.
However, when reproduced on the board, this new technique did not require mental trial-and-error computations nor complex carry memorization (unlike base 10 computations). He was so pleased by his discovery that he said in his preface:
it might be well described as more of a lark than a labor, for it carries out addition, subtraction, multiplication, division and the extraction of square roots purely by moving counters from place to place.
Location numerals
Binary notation had not yet been standardized, so Napier used what he called location numerals to represent binary numbers. Napier's system uses sign-value notation to represent numbers; it uses successive letters from the Latin alphabet to represent successive powers of two: a = 20 = 1, b = 21 = 2, c = 22 = 4, d = 23 = 8, e = 24 = 16 and so on.
To represent a given number as a location numeral, that number is expressed as a sum of powers of two and then each power of two is replaced by its corresponding digit (letter). For example, when converting from a decimal numeral:
- 87 = 1 + 2 + 4 + 16 + 64 = 20 + 21 + 22 + 24 + 26 = abceg
Using the reverse process, a location numeral can be converted to another numeral system. For example, when converting to a decimal numeral:
- abdgkl = 20 + 21 + 23 + 26 + 210 + 211 = 1 + 2 + 8 + 64 + 1024 + 2048 = 3147
Napier showed multiple methods of converting numbers in and out of his numeral system. These methods are similar to modern methods of converting numbers in and out of the binary numeral system, so they are not shown here. Napier also showed how to add, subtract, multiply, divide, and extract square roots.
Abbreviated and extended form
As in any numeral system using sign-value notation (but not those using positional notation), digits (letters) can be repeated such that multiple numerals can represent a single number. For example:
- abbc = acc = ad = 9
Additionally, the order of digits does not matter. For example:
- abbc = bbca = bcba = ... = 9
Because each digit in a location numeral represents twice the value of its next-lower digit, replacing any two occurrences of the same digit with one of the next-higher digit does not change the numeral's numeric value. Thus, repeatedly applying the rules of replacement aa → b, bb → c, cc → d, etc. to a location numeral removes all repeated digits from that numeral.
Napier called this process abbreviation and the resulting location numeral the abbreviated form of that numeral; he called location numerals containing repeated digits extended forms. Each number can be represented by a unique abbreviated form, not considering the order of its digits (e.g., abc, bca, cba, etc. all represent the number 7).
Arithmetic
Addition
Location numerals allow for a simple and intuitive algorithm for addition:
- join the numerals end-to-end
- when necessary, rearrange this conjoined numeral's digits so they are in ascending order
- abbreviate this rearranged and conjoined numeral
For example, to add 157 = acdeh and 230 = bcfgh, join the numerals end-to-end:
- acdeh + bcfgh → acdehbcfgh
rearrange the digits of the previous result (because the digits of acdehbcfgh are not in ascending order):
- acdehbcfgh → abccdefghh
and abbreviate the previous result:
- abccdefghh → abddefghh → abeefghh → abffghh → abgghh → abhhh → abhi
The final result, abhi, equals 387 (abhi = 20 + 21 + 27 + 28 = 1 + 2 + 128 + 256 = 387); this is the same result achieved by adding 157 and 230 in decimal notation.
Subtraction
Subtraction is also intuitive, but may require expanding abbreviated forms to extended forms to perform borrows.
Write the minuend (the largest number you want to diminish) and remove from it all the digits appearing in the subtrahend (the smallest number). In case the digit to be removed does not appear in the minuend, then borrow it by expanding the unit just larger. Repeat until all the digit of the subtrahend have been removed.
A few examples show it is simpler than it sounds :
- Subtract 5 = ac from 77 = acdg :
- acdg - ac =
acdg = dg = 8+64 = 72.
- Subtract 3 = ab from 77 = acdg :
- acdg - ab = abbdg - ab =
abbdg = bdg = 2+8+64 = 74.
- Subtract 7 = abc from 77 = acdg :
- acdg - abc = abbccg - abc =
abbccg = bcg = 2+4+64 = 70.
Doubling, halving, odd and even
Napier proceeded to the rest of arithmetic, that is multiplication, division and square root, on an abacus, as it was common in his times. However, since the development of micro-processor computer, a lot of applicable algorithms have been developed or revived based on doubling and halving.
Doubling is done by adding a numeral to itself, which mean doubling each of its digit. This gives an extended form, which has to be abbreviated if needed. This operation can be done in one step by changing each digit of a numeral to the next larger digit. For example, the double of a is b, the double of b is c, the double of ab is bc, the double of acfg is bdgh, etc.
Similarly, multiplying by a power of two, is just translating its digits. To multiply by c = 4, forexample, is transforming the digits a → c, b → d, c → e,...
Halving is the reverse of doubling: change each digit to the next smaller digit. For example, the half of bdgh is acfg.
One sees immediately that it is only feasible when the numeral to be halved does not contain an a (or, if the numeral is extended, an odd number of as). In other words, an abbreviated numeral is odd if it contains an a and even if it does not.
With these basic operations (doubling and halving), we can adapt all the binary algorithms starting by, but not limited to, the Bisection method and Dichotomic search.
Multiplication
Napier performed multiplication and division on an abacus, as was common in his times. However, Egyptian multiplication gives an elegant way to carry out multiplication without tables using only doubling, halving and adding.
Multiplying a single-digit number by another single-digit number is a simple process. Because all letters represent a power of 2, multiplying digits is the same as adding their exponents. This can also be thought of as finding the index of one digit in the alphabet (a = 0, b = 1, ...) and incrementing the other digit by that amount in terms of the alphabet (b + 2 => d).
For example, multiply 4 = c by 16 = e
c * e = 2^2 * 2^4 = 2^6 = g
or...
AlphabetIndex(c) = 2, so... e => f => g
To find the product of two multiple digit numbers, make a two column table. In the left column write the digits of the first number, one below the other. For each digit in the left column, multiply that digit and the second number and record it in the right column. Finally, add all the numbers of the right column together.
As an example, multiply 238 = bcdfgh by 13 = acd
a bcdfgh c defhij d efgijk
The result is the sum in the right column bcdfgh defhij efgijk = bcddeefffgghhiijjk = bcekl = 2+4+16+1024+2048 = 3094.
It is interesting to notice that the left column can also be obtained by successive halves of the first number, from which the even numbers are removed. In our example, acd, bc (even), ab, a. Noticing that the right column contains successive doubles of the second number, shows why the peasant multiplication is exact.
Division, remainder
Division can be carried out by successive subtractions: the quotient is the number of time the divisor can be subtracted from the dividend, and the remainder is what is left rest after all the possible subtractions.
This process, which can be very long, may be made efficient if instead of the divisor we subtract multiple of the divisor, and computations are easier if we restrict to multiple by a power of 2.
In fact, this is what we do in the long division method.
The grid
Location arithmetic uses a square grid where each square on the grid represents a value. Two sides of the grid are marked with increasing powers of two. Any inner square can be identified by two numbers on these two sides, one being vertically below the inner square and the other to its far right. The value of the square is the product of these two numbers.
| 32 | ||||||
| 16 | ||||||
| 8 | ||||||
| 32 | 4 | |||||
| 2 | ||||||
| 1 | ||||||
| 32 | 16 | 8 | 4 | 2 | 1 |
For instance, the square in this example grid represents 32, as it is the product of 4 on the right column and 8 from the bottom row. The grid itself can be any size, and larger grids simply permit us to handle larger numbers.
Notice that moving either one square to the left or one square up doubles the value. This property can be used to perform binary addition using just a single row of the grid.
Addition
First, lay out a binary number on a row using counters to represent the 1s in the number. For example, 29 (= 11101 in binary) would be placed on the board like this:
| 0 | 1 | 1 | 1 | 0 | 1 |
The number 29 is clearly the sum of the values of the squares on which there are counters. Now overlay the second number on this row. Say we place 9 (= 1001 in binary) on it like this.
| 0 | 0 | 1 | 0 | 0 | 1 |
The sum of these two numbers is just the total value represented by the counters on the board, but some of the squares have more than one counter. Recall however, that moving to the left of a square doubles its value. So we replace two counters on a square with one counter to its left without changing the total value on the board. Note that this is the same idea used to abbreviate location numerals. Let's start by replacing the rightmost pair of counters with a counter to its left, giving:
| ← |
We still have another square with two counters on it, so we do it again:
| ← |
But replacing this pair created another square with two counters on it, so we replace a third time:
| ← | |||||
| 1 | 0 | 0 | 1 | 1 | 0 |
Now each square has just one counter, and reading off the result in binary 100110 (= 38) gives the correct result.
Subtraction
Subtracting is not much more complicated than addition: instead of adding counters on the board we remove them. To "borrow" a value, we replace a counter on a square with two to its right.
Let's see how we might subtract 12 from 38. First place 38 (= 100110 in binary) on a row, and then place 12 (= 1100 in binary) under it:
| 38 | ||||||
| 12 |
For every counter on the lower row that has a counter above it, remove both counters. We can remove one such pair on the board, resulting in:
| ↓ | |||||
| ↓ |
Now we need to "borrow" counters to get rid of the remaining counter on the bottom. First replace the leftmost counter on the top row with two to its right:
| → | |||||
Now replace one of the two counters with two more to its right, giving:
We can now take away one of the counters on the top row with the remaining counter on the bottom row:
| ↓ |
and read off 26, the final result.
Some properties of the grid
Unlike addition and subtraction, the entire grid is used to multiply, divide, and extract square roots. The grid has some useful properties utilized in these operations. First, all the squares on any diagonal going from the bottom left to the top right have the same value.
| 256 | 32 | |||||
| 256 | 16 | 16 | ||||
| 256 | 16 | 8 | ||||
| 16 | 4 | |||||
| 16 | 2 | |||||
| 16 | 1 | |||||
| 32 | 16 | 8 | 4 | 2 | 1 |
Since a diagonal move can be broken down into a move to the right (which halves the value) followed by a move up (which doubles the value), the value of the square stays the same.
In conjunction with that diagonal property, there is a quick way to divide the numbers on the bottom and right edges of the grid.
| 32 | ||||||
| 16 | ||||||
| 8 | ||||||
| → | → | → | 4 | |||
| 2 | ||||||
| 1 | ||||||
| 32 | 16 | 8 | 4 | 2 | 1 |
Locate the dividend 32 along the right side and the divisor 8 on the bottom edge of the grid. Extend a diagonal from the dividend and locate the square where it intersects a vertical line from the divisor. The quotient lies at the right end of the grid from this square, which for our example is 4.
Why does this work? Moving along the diagonal does not change the value; the value of the square on the intersection is still the dividend. But we also know it is the product of the squares along the bottom and right edge. Since the square on the bottom edge is the divisor, the square on the right edge is the quotient.
Napier extends this idea to divide two arbitrary numbers, as shown below.
Multiplication
To multiply a pair of binary numbers, first mark the two numbers on the bottom and the right side of the grid. Say we want to multiply 22 (= 10110) by 9 (= 1001).
| 1 | ||||||
| 0 | ||||||
| 0 | ||||||
| 1 | ||||||
| 1 | 0 | 1 | 1 | 0 |
Now place counters at every "intersection" of vertical and horizontal rows of the 1s in each number.
| 1 | ||||||
| 0 | ||||||
| 0 | ||||||
| 1 | ||||||
| 1 | 0 | 1 | 1 | 0 |
Notice that each row of counters on the grid is just 22 multiplied by some power of two. In fact, the total value of the counters is the sum of two rows
- 22*8 + 22*1 = 22*(8+1) = 22*9
So the counters on the board actually represent the product of the two numbers, except it is not possible to "read off" the answer just yet.
Recall that moving counters diagonally does not change the value, so move all the counters on inner squares diagonally until they hit either the bottom row or the left column.
Now we make the same moves we did for addition. Replace two counters on a square with one to its left. If the square is on the left column, replace two counters with one above it. Recall that the value of a square doubles if you move up, so this does not change the value on the grid.
Let's first replace the two counters on the second square at the bottom with one to its left which leaves two counters at the corner.
| ← |
Finally, replace the two counters on the corner with one above it and "read off" the binary number in an L-shaped fashion, starting from the top left down to the bottom left corner, and then over to the bottom right.
| 1 | ||||||
| 1 | ||||||
| ↑ | ||||||
| 0 | 0 | 0 | 1 | 1 | 0 |
Read the counters along the L but do not double count the corner square. You will read the binary result 11000110 = 198 which is indeed 22*9.
Why can we read the binary number in this L-shaped fashion? The bottom row is of course just the first six powers of two, but notice that the leftmost column has the next five powers of two. So we can directly read off an 11 digit binary number from the L-shaped set of 11 squares that lie along the left and bottom sides of the grid.
| 1024 | ↓ | |||||
| 512 | ↓ | |||||
| 256 | ↓ | |||||
| 128 | ↓ | |||||
| 64 | ↓ | |||||
| → | → | → | → | → | → | |
| 32 | 16 | 8 | 4 | 2 | 1 |
Our small 6x6 grid can only multiply numbers each up to 63, and in general an nxn grid can multiply two numbers each up to 2n-1. This scales very fast, so board with 20 numbers per side, for instance, can multiply numbers each up to a little over one million.
Division
Martin Gardner presented a slightly easier to understand version of Napier's division method, which is what is shown here.
Division works pretty much the reverse of multiplication. Say we want to divide 485 by 13. First place counters for 485 (= 111100101) along the bottom edge and mark 13 (= 1101) along the right edge. To save space, we'll just look at a rectangular portion of the board because that's all we actually use.
| 1 | |||||||||
| 1 | |||||||||
| 0 | |||||||||
| 1 | |||||||||
Starting from the left, the game is to move counters diagonally into "columns of divisors" (that is, with one counter on each row marked with a 1 from the divisor.) Let's demonstrate this with the leftmost block of counters.
| 1 | |||||||||
| 1 | |||||||||
| 0 | |||||||||
| 1 | |||||||||
| ↑ |
Now the next block of counters we might try would begin with the leftmost counter on the bottom, and we might attempt something like
| 1 | |||||||||
| ? | 1 | ||||||||
| 0 | |||||||||
| ? | 1 | ||||||||
except that we do not have any counters that we can move diagonally from the bottom edge into squares that would form the rest of the "column of divisors."
In such cases, we instead "double down" the counter on the bottom row and form a column one over to the right. As you will soon see, it will always be possible to form a column this way. So first replace the counter on the bottom with two to its right.
| 1 | |||||||||
| 1 | |||||||||
| 0 | |||||||||
| 1 | |||||||||
| → |
and then move one diagonally to the top of the column, and move another counter located on the edge of the board into its spot.
| 1 | |||||||||
| ? | 1 | ||||||||
| 0 | |||||||||
| 1 | |||||||||
| ↑ |
It looks like we still do not have a counter on the bottom edge to move diagonally into the remaining square, but notice that we can instead double down the leftmost counter again and then move it into the desired square.
| 1 | |||||||||
| ? | 1 | ||||||||
| 0 | |||||||||
| 1 | |||||||||
| → |
and now move one counter diagonally to where we want it.
| 1 | |||||||||
| 1 | |||||||||
| 0 | |||||||||
| 1 | |||||||||
Let's proceed to build the next column. Once again, notice that moving the leftmost counter to the top of the column does not leave enough counters at the bottom to fill in the remaining squares.
| 1 | |||||||||
| ? | 1 | ||||||||
| 0 | |||||||||
| ? | 1 | ||||||||
So we double down the counter and move one diagonally into the next column over. Let's also move the rightmost counter into the column, and here is how it looks after these steps.
| 1 | |||||||||
| ? | 1 | ||||||||
| 0 | |||||||||
| 1 | |||||||||
| → | ↑ |
We still have a missing square, but we just double down again and move the counter into this spot and end up with
| 1 | 0 | 0 | 1 | 0 | 1 | ||||
| 1 | |||||||||
| 1 | |||||||||
| 0 | |||||||||
| 1 | |||||||||
| → |
At this point, the counter on the bottom edge is so far to the right that it cannot go diagonally to the top of any column, which signals that we are done.
The result is "read" off the columns—each column with counters is treated as a 1 and empty columns are 0. So the result is 100101 (= 37) and the remainder is the binary value of any counters still left along the bottom edge. There is one counter on the third column from the right, so we read it as 100 (= 4) and we get 485 ÷ 13 = 37 with a remainder 4.
Square roots
Napier's Method

This process requires one to add counters to the abacus (board) to make square figures. The top of page 149 shows diagrams that explain this process. Begin by placing a single counter on the board (it will actually go on one of the dotted squares). Adding three other counters adjacent (or with blank rows and columns between them and the first one placed) will result in another square figure on the abacus. Similarly adding another five counters to this (with or without the blank rows and columns shown) will result in an even bigger square. Take the number to be considered and put counters along one margin that represent its value. From the position of the largest counter in that value, follow the diagonal lines (bishop’s moves) across the board until you come to a square with a dot. Place a counter on that square. Subtract the value represented by this single counter from the original number in the margin. Add three (five, seven, ... for subsequent steps) to create a square on the board and subtract the value of the added counters from the number in the margin until the number is either too large to be subtracted or there is no space left on the board. You should be left with a large square of counters (perhaps with blank rows and columns between them) on the board. Move one of the counters in each row of the square to the margin and the positions of these marginal counters will yield the square root of the number.

Napier provides an example of determining the square root of 1238. The largest counter is in the 1024 position so the first counter is placed on the dot found by moving down the 1024 diagonal (at the 32,32 position). Subtracting this value (1024) from the original number leaves counters at 128, 64, 16, 4 and 2 (= 214). Placing three counters on the board to form a square with the first counter but whose value can still be subtracted from 214, results in counters at positions 32,2; 2,2; and 2,32 (whose values are 64, 4 and 64, which when subtracted from the remainder of 214 = 82. The next square that can be constructed from five counters, yet the values of those five counters still being capable of being subtracted from 82 results in counters in positions 32,1; 2,1; 1,1; 1.2; and 1,32. The values of these five counters total 69 which when subtracted from 82 leave 13 as a remainder. As there is no more room on the board we have to stop. Move one counter from each row to the margin (rows 32, 2 and 1) and this value (35) is the square root required, or at least the integer part of it (the actual value is 35.1852....).
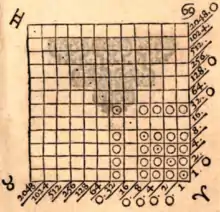
Napier provides a second example for calculating the square root of 2209 (= 47). [1]
See also
References
- ^ John Napier; translated by William Frank Richardson; introduction by Robin E. Rider (1990). Rabdology. MIT Press. ISBN 0-262-14046-2.
- ^ Martin Gardner (1986). Knotted doughnuts and other mathematical entertainments. W. H. Freeman and Company. ISBN 0-7167-1794-8.
- Specific