Lyra2 is a password hashing scheme (PHS) that can also work as a key derivation function (KDF). It received a special recognition during the Password Hashing Competition in July 2015,[1] which was won by Argon2. Besides being used for its original purposes, it is also in the core of proof-of-work algorithms such as Lyra2REv2,[2] adopted by Vertcoin,[3] MonaCoin,[4] among other cryptocurrencies[5] Lyra2 was designed by Marcos A. Simplicio Jr., Leonardo C. Almeida, Ewerton R. Andrade, Paulo C. F. dos Santos, and Paulo S. L. M. Barreto from Escola Politécnica da Universidade de São Paulo.[6] It is an improvement over Lyra,[7][8] previously proposed by the same authors. Lyra2 preserves the security, efficiency and flexibility of its predecessor, including: (1) the ability to configure the desired amount of memory, processing time and parallelism to be used by the algorithm; and (2) the capacity of providing a high memory usage with a processing time similar to that obtained with scrypt. In addition, it brings the following improvements when compared to its predecessor:[9]
- it allows a higher security level against attack venues involving time-memory trade-offs
- it allows legitimate users to benefit more effectively from the parallelism capabilities of their own platforms
- it includes tweaks for increasing the costs involved in the construction of dedicated hardware to attack the algorithm
- it balances resistance against side-channel threats and attacks relying on cheaper hence, slower storage devices
- Lyra2 is released under public domain, and provides two main extensions:[10]
- Lyra2-δ, gives the user better control over the algorithm's bandwidth usage
- Lyra2p, takes advantage of parallelism capabilities on the legitimate user's platform
This algorithm enables parameterization in terms of:[10]
- execution time (time cost )
- memory required (number of rows , and number of columns )
- degree of parallelism (number of threads )
- underlying permutation function (can be seen as the main cryptographic primitive)
- number of blocks used by the underlying permutation function (bitrate)
- number of rounds performed for the underlying permutation function ()
- number of bits to be used in rotations ()
- output length ()
Strengths
The main strengths of the algorithm are:[5][10]
- High resistance against processing-memory tradeoffs: estimated processing costs of attacks with low memory usage involve a factor that grows exponentially with time cost due to recomputations
- Memory and time costs can be decoupled, allowing their usage to be fine-tuned
- Fast due to use of reduced-round sponge function in the algorithm's core
- Can provide outputs of any desired length, behaving as a key derivation function (KDF)
- Design combines resistance to side-channel attacks (during the whole Setup phase) and to attacks involving cheap (hence, low-speed) memory devices, aiming to balance such conflicting requirements
- Considers a wide range of configurations for protecting against attacking platforms while optimizing execution on legitimate platform, such as:
- Support for parallelism, for multi-core platforms, without giving much advantage to GPU-based attacks
- Capability of using different underlying sponge functions depending on the target platform (e.g., BLAKE2b for software implementations; Keccak for hardware implementations; BlaMka for additional resistance against hardware platforms; etc.)
- Ability to raise the algorithm's memory bandwidth usage (note: the original specification is expected to max out the bandwidth in current machines, but feature may be useful for future hardware)
Design
As any PHS, Lyra2 takes as input a salt and a password, creating a pseudorandom output that can then be used as key material for cryptographic algorithms or as an authentication string.[11]
Internally, the scheme's memory is organized as a matrix that is expected to remain in memory during the whole password hashing process: since its cells are iteratively read and written, discarding a cell for saving memory leads to the need of recomputing it whenever it is accessed once again, until the point it was last modified.[5]
The construction and visitation of the matrix is done using a stateful combination of the absorbing, squeezing and duplexing operations of the underlying sponge (i.e., its internal state is never reset to zero), ensuring the sequential nature of the whole process.
Also, the number of times the matrix's cells are revisited after initialization is defined by the user, allowing Lyra2's execution time to be fine-tuned according to the target platform's resources.
Functions/symbols
|| Concatenate two strings
^ Bitwise XOR
[+] Wordwise add operation (i.e., ignoring carries between words)
% Modulus
W The target machine's word size (usually, 32 or 64)
omega Number of bits to be used in rotations (recommended: a multiple of the machine's word size, W)
>>> Right rotation
rho Number of rounds for reduced squeeze or duplexing operations
blen Sponge's block size in bytes
H or H_i Sponge with block size blen (in bytes) and underlying permutation f
H.absorb(input) Sponge's absorb operation on input
H.squeeze(len) Sponge's squeeze operation of len bytes
H.squeeze_{rho}(len) Sponge's squeeze operation of len bytes using rho rounds of f
H.duplexing(input,len) Sponge's duplexing operation on input, producing len bytes
H.duplexing_{rho}(input,len) Sponge's duplexing operation on input, using rho rounds of f, producing len bytes
pad(string) Pads a string to a multiple of blen bytes (padding rule: 10*1)
lsw(input) The least significant word of input
len(string) Length of a string, in bytes
syncThreads() Synchronize parallel threads
swap(input1,input2) Swap the value of two inputs
C Number of columns on the memory matrix (usually, 64, 128, 256, 512 or 1024)
P Degree of parallelism (P >= 1 and (m_cost/2) % P = 0)
Inputs
- password
- salt
- t_cost
- m_cost
- outlen
Algorithm without parallelism
** Bootstrapping phase: Initializes the sponge's state and local variables
# Byte representation of input parameters (others can be added)
params = outlen || len(password) || len(salt) || t_cost || m_cost || C
# Initializes the sponge's state (after that, password can be overwritten)
H.absorb( pad(password || salt || params) )
# Initializes visitation step, window and first rows that will feed
gap = 1
stp = 1
wnd = 2
sqrt = 2
prev0 = 2
row1 = 1
prev1 = 0
** Setup phase: Initializes a (m_cost x C) memory matrix, its cells having blen-byte cells
# Initializes M[0], M[1] and M[2]
for col = 0 to C-1
M[0][C-1-col] = H.squeeze_{rho}(blen)
for col = 0 to C-1
M[1][C-1-col] = H.duplexing_{rho}( M[0][col], blen)
for col = 0 to C-1
M[2][C-1-col] = H.duplexing_{rho}( M[1][col], blen)
# Filling Loop: initializes remainder rows
for row0 = 3 to m_cost-1
# Columns Loop: M[row0] is initialized and M[row1] is updated
for col = 0 to C-1
rand = H.duplexing_{rho}( M[row1][col] [+] M[prev0][col] [+] M[prev1][col], blen)
M[row0][C-1-col] = M[prev0][col] ^ rand
M[row1][col] = M[row1][col] ^ ( rand >>> omega )
# Rows to be revisited in next loop
prev0 = row0
prev1 = row1
row1 = (row1 + stp) % wnd
# Window fully revisited
if (row1 = 0)
# Doubles window and adjusts step
wnd = 2 * wnd
stp = sqrt + gap
gap = -gap
# Doubles sqrt every other iteration
if (gap = -1)
sqrt = 2 * sqrt
** Wandering phase: Iteratively overwrites pseudorandom cells of the memory matrix
# Visitation Loop: (2 * m_cost * t_cost) rows revisited in pseudorandom fashion
for wCount = 0 to ( (m_cost * t_cost) - 1)
# Picks pseudorandom rows
row0 = lsw(rand) % m_cost
row1 = lsw( rand >>> omega ) % m_cost
# Columns Loop: updates both M[row0] and M[row1]
for col = 0 to C-1
# Picks pseudorandom columns
col0 = lsw( ( rand >>> omega ) >>> omega ) % C
col1 = lsw( ( ( rand >>> omega ) >>> omega ) >>> omega ) % C
rand = H.duplexing_{rho}( M[row0][col] [+] M[row1][col] [+] M[prev0][col0] [+] M[prev1][col1], blen)
M[row0][col] = M[row0][col] ^ rand
M[row1][col] = M[row1][col] ^ ( rand >>> omega )
# Next iteration revisits most recently updated rows
prev0 = row0
prev1 = row1
** Wrap-up phase: output computation
# Absorbs a final column with a full-round sponge
H.absorb( M[row0][0] )
# Squeezes outlen bits with a full-round sponge
output = H.squeeze(outlen)
# Provides outlen-long bitstring as output
return output
Algorithm with parallelism
for each i in [0..P]
** Bootstrapping phase: Initializes the sponge's state and local variables
# Byte representation of input parameters (others can be added)
params = outlen || len(password) || len(salt) || t_cost || m_cost || C || P || i
# Initializes the sponge's state (after that, password can be overwritten)
H_i.absorb( pad(password || salt || params) )
# Initializes visitation step, window and first rows that will feed
gap = 1
stp = 1
wnd = 2
sqrt = 2
sync = 4
j = i
prev0 = 2
rowP = 1
prevP = 0
** Setup phase: Initializes a (m_cost x C) memory matrix, its cells having blen-byte cells
# Initializes M_i[0], M_i[1] and M_i[2]
for col = 0 to C-1
M_i[0][C-1-col] = H_i.squeeze_{rho}(blen)
for col = 0 to C-1
M_i[1][C-1-col] = H_i.duplexing_{rho}( M_i[0][col], blen)
for col = 0 to C-1
M_i[2][C-1-col] = H_i.duplexing_{rho}( M_i[1][col], blen)
# Filling Loop: initializes remainder rows
for row0 = 3 to ( (m_cost / P) - 1 )
# Columns Loop: M_i[row0] is initialized and M_j[row1] is updated
for col = 0 to C-1
rand = H_i.duplexing_{rho}( M_j[rowP][col] [+] M_i[prev0][col] [+] M_j[prevP][col], blen)
M_i[row0][C-1-col] = M_i[prev0][col] ^ rand
M_j[rowP][col] = M_j[rowP][col] ^ ( rand >>> omega )
# Rows to be revisited in next loop
prev0 = row0
prevP = rowP
rowP = (rowP + stp) % wnd
# Window fully revisited
if (rowP = 0)
# Doubles window and adjusts step
wnd = 2 * wnd
stp = sqrt + gap
gap = -gap
# Doubles sqrt every other iteration
if (gap = -1)
sqrt = 2 * sqrt
# Synchronize point
if (row0 = sync)
sync = sync + (sqrt / 2)
j = (j + 1) % P
syncThreads()
syncThreads()
** Wandering phase: Iteratively overwrites pseudorandom cells of the memory matrix
wnd = m_cost / (2 * P)
sync = sqrt
off0 = 0
offP = wnd
# Visitation Loop: (2 * m_cost * t_cost / P) rows revisited in pseudorandom fashion
for wCount = 0 to ( ( (m_cost * t_cost) / P) - 1)
# Picks pseudorandom rows and slices (j)
row0 = off0 + (lsw(rand) % wnd)
rowP = offP + (lsw( rand >>> omega ) % wnd)
j = lsw( ( rand >>> omega ) >>> omega ) % P
# Columns Loop: update M_i[row0]
for col = 0 to C-1
# Picks pseudorandom column
col0 = lsw( ( ( rand >>> omega ) >>> omega ) >>> omega ) % C
rand = H_i.duplexing_{rho}( M_i[row0][col] [+] M_i[prev0][col0] [+] M_j[rowP][col], blen)
M_i[row0][col] = M_i[row0][col] ^ rand
# Next iteration revisits most recently updated rows
prev0 = row0
# Synchronize point
if (wCount = sync)
sync = sync + sqrt
swap(off0,offP)
syncThreads()
syncThreads()
** Wrap-up phase: output computation
# Absorbs a final column with a full-round sponge
H_i.absorb( M_i[row0][0] )
# Squeezes outlen bits with a full-round sponge
output_i = H_i.squeeze(outlen)
# Provides outlen-long bitstring as output
return output_0 ^ ... ^ output_{P-1}
Security analysis
Against Lyra2, the processing cost of attacks using of the amount of memory employed by a legitimate user is expected to be between and , the latter being a better estimate for , instead of the achieved when the amount of memory is , where is a user-defined parameter to define a processing time.
This compares well to Scrypt, which displays a cost of when the memory usage is ,[12] and with other solutions in the literature, for which the results are usually .[7][13][14][15]
Nonetheless, in practice these solutions usually involve a value of (memory usage) lower than those attained with the Lyra2 for the same processing time.[16][17][18][19][20]
Performance
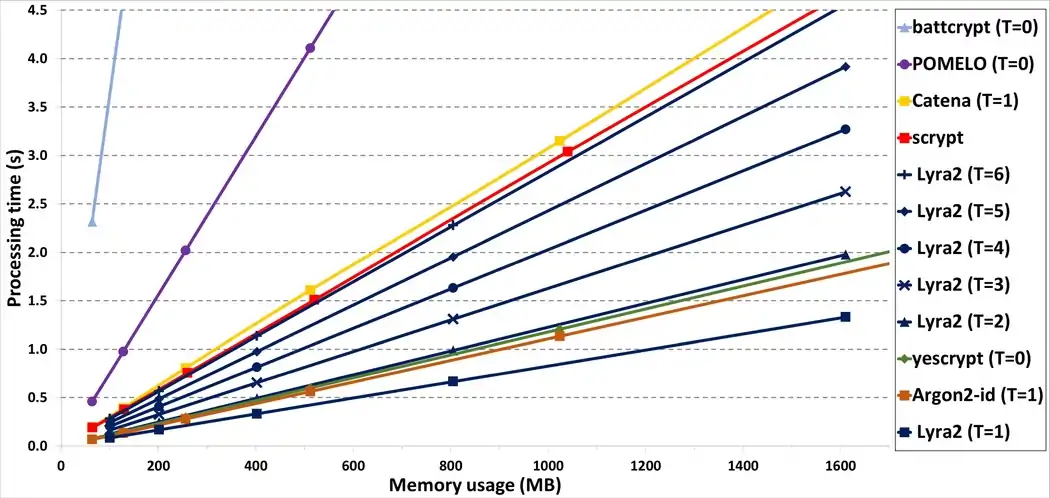
The processing time obtained with a SSE single-core implementation of Lyra2 are illustrated in the hereby shown figure. This figure was extracted from,[9] and is very similar of third-party benchmarks performed during the PHC context.[16][17][18][19][20]
The results depicted correspond to the average execution time of Lyra2 configured with , , bits (i.e., the inner state has 256 bits), and different and settings, giving an overall idea of possible combinations of parameters and the corresponding usage of resources.
As shown in this figure, Lyra2 is able to execute in: less than 1 s while using up to 400 MB (with and ) or up to 1 GB of memory (with and ); or in less than 5 s with 1.6 GB (with and ).
All tests were performed on an Intel Xeon E5-2430 (2.20 GHz with 12 Cores, 64 bits) equipped with 48 GB of DRAM, running Ubuntu 14.04 LTS 64 bits, and the source code was compiled using gcc 4.9.2.[9]
References
- ↑ "Password Hashing Competition". password-hashing.net. Retrieved 2016-03-22.
- ↑ "Lyra2REv2". eprint.iacr.org. Retrieved 2016-03-22.
- ↑ "Vertcoin". vertcoin.org. Retrieved 2019-10-08.
- ↑ "MonaCoin". monacoin.org. Retrieved 2019-10-08.
- 1 2 3 van Beirendonck, M.; Trudeau, L.; Giard, P.; Balatsoukas-Stimming, A. (2019-05-29). A Lyra2 FPGA Core for Lyra2REv2-Based Cryptocurrencies. IEEE International Symposium on Circuits and Systems (ISCAS). Sapporo, Japan: IEEE. pp. 1–5. arXiv:1807.05764. doi:10.1109/ISCAS.2019.8702498.
- ↑ "Cryptology ePrint Archive: Report 2015/136". eprint.iacr.org. Retrieved 2016-03-22.
- 1 2 Almeida, Leonardo C.; Andrade, Ewerton R.; Barreto, Paulo S. L. M.; Simplicio Jr, Marcos A. (2014-01-04). "Lyra: password-based key derivation with tunable memory and processing costs". Journal of Cryptographic Engineering. 4 (2): 75–89. CiteSeerX 10.1.1.642.8519. doi:10.1007/s13389-013-0063-5. ISSN 2190-8508. S2CID 5245769.
- ↑ "Cryptology ePrint Archive: Report 2014/030". eprint.iacr.org. Retrieved 2016-03-22.
- 1 2 3 Andrade, E.; Simplicio Jr, M.; Barreto, P.; Santos, P. (2016-01-01). "Lyra2: efficient password hashing with high security against time-memory trade-offs". IEEE Transactions on Computers. PP (99): 3096–3108. doi:10.1109/TC.2016.2516011. ISSN 0018-9340. S2CID 37232444.
- 1 2 3 Simplicio Jr, Marcos A.; Almeida, Leonardo C.; Andrade, Ewerton R.; Santos, Paulo C.; Barreto, Paulo S. L. M. "The Lyra2 reference guide" (PDF). PHC. The Password Hashing Competition.
- ↑ Chen, Lily (2009). "Recommendation for Key Derivation Using Pseudorandom Functions (Revised)" (PDF). Computer Security. NIST. doi:10.6028/NIST.SP.800-108.
- ↑ Percival, Colin. "Stronger Key Derivation via Sequential Memory-Hard Functions" (PDF). TARSNAP. The Technical BSD Conference.
- ↑ "Cryptology ePrint Archive: Report 2013/525". eprint.iacr.org. Retrieved 2016-03-22.
- ↑ Schmidt, Sascha. "Implementation of the Catena Password-Scrambling Framework" (PDF). Bauhaus-Universität Weimar. Faculty of Media.
- ↑ "P-H-C/phc-winner-argon2" (PDF). GitHub. Retrieved 2016-03-22.
- 1 2 "Gmane -- Another PHC candidates mechanical tests". article.gmane.org. Retrieved 2016-03-22.
- 1 2 "Gmane -- A review per day Lyra2". article.gmane.org. Retrieved 2016-03-22.
- 1 2 "Gmane -- Lyra2 initial review". article.gmane.org. Retrieved 2016-03-22.
- 1 2 "Gmane -- Memory performance and ASIC attacks". article.gmane.org. Retrieved 2016-03-22.
- 1 2 "Gmane -- Quick analysis of Argon". article.gmane.org. Retrieved 2016-03-22.