Main path analysis is a mathematical tool, first proposed by Hummon and Doreian in 1989,[1] to identify the major paths in a citation network, which is one form of a directed acyclic graph (DAG). It has since become an effective technique for mapping technological trajectories, exploring scientific knowledge flows, and conducting literature reviews.

The method begins by measuring the significance of all the links in a citation network through the concept of ‘traversal count’ and then sequentially chains the most significant links into a "main path", which is deemed the most significant historical path in the target citation network. The method is applicable to any human activity that can be organized in the form of a citation network. The method is commonly applied to trace the knowledge flow paths or development trajectories of a science or technology field, through bibliographic citations or patent citations.[2][3][4] It has also been applied to judicial decisions to trace the evolving changes of legal opinions.[5] Main path analysis has attracted scholars attention recently. Academic research related to main path analysis saw a fast growing since 2007. A list of academic articles that introduce, explain, apply, modify, or extend the method originated in Hummon and Doreian[1] can be found here. Nevertheless, there are issues not broadly discussed in applying the method, including the handling of citation data, choosing a proper traversal weight scheme, search options, and interpretation of the resulting paths.[6]
History
Main path analysis is first proposed in Hummon and Doreian (1989)[1] in which they suggest a different approach for analyzing a citation network "where the connective threads through a network are preserved and the focus is on the links in the network rather than on the nodes."[1] They call the resulting chain of the most used citation links "main path" and claim that "It is our intuition that the main path, selected on the basis of the most used path will identify the main stream of a literature." The idea was verified using a set of DNA research articles. To make the method more practical, Liu and Lu (2012)[7] extends the method to include the key-route search. The most useful feature of the key-route search is that one is able to view the different level of main paths by adjusting the key-route numbers.
The method
Main path analysis operates in two steps. The first step obtains the traversal counts of each link in a citation network. Several types of traversal counts are mentioned in the literature. The second step searches for the main paths by linking the significant links according to the size of traversal counts. One needs to prepare a citation network before proceeding for main path analysis.
Preparing a citation network
It is necessary to prepare a citation network before starting main path analysis. In a citation network, the nodes represent the documents such as academic articles, patents, or legal cases. These nodes are connected using citation information. Citation networks are by nature directed because the two nodes on the opposite end of a link are not symmetrical in their roles. As regards to the direction, this article adopts the convention that the cited node points to the citing node, signifying the fact that knowledge in the cited node flows to the citing node. Citation network is also by nature acyclic, which means that a node can never chain back to itself if one moves along the links following their direction.
Several terms related to a citation network are defined here before proceeding further. Heads are the nodes the direction arrow leads to. Tails are the nodes on other ends of the direction arrow. Sources are the nodes that are cited but cite no others. Sinks cite other nodes but are not cited. Ancestors are the nodes that can be traced back to from a target node. Descendants are the nodes that one can reach from a target if one moves along the links following their direction.

Traversal counts
Traversal counts measure the significance of a link. The literature discusses several types of traversal counts, including search path count (SPC), search path link count (SPLC), search path node pair (SPNP), and other variations.[8] All these traversal counts will be noted as SPX.

Search path count (SPC)
A link’s SPC is the number of times the link is traversed if one runs through all possible paths from all the sources to all the sinks. SPC is first proposed by Vladimir Batagelj.[9] SPC values for each link in a sample citation network is shown in Figure 1. The SPC value for the link (B, D) is 5 because five paths (B-D-F-H-K, B-D-F-I-L, B-D-F-I-M-N, B-D-I-L, and B-D-I-M-N) traverse through it.

Search path link count (SPLC)
A link’s SPLC is the number of times the link is traversed if one runs through all possible paths from all the ancestors of the tail node (including itself) to all the sinks. SPLC is first proposed by Hummon and Doreian.[1] Figure 2 presents the SPLC values for each link in the same citation network as shown in Figure 1. Six paths traverse through the link (D, F) thus give it the SPLC value 6. They are: B-D-F-H-K, B-D-F-I-L, B-D-F-I-M-N, D-F-H-K, D-F-I-L, and D-F-I-M-N, noting that all the paths begin either from the ancestor of D, which is B, and D itself.
Search path node pair (SPNP)
A link’s SPNP is the number of times the link is traversed if one runs through all possible paths from all the ancestors of the tail node (including itself) to all the descendants of the head node (including itself). SPNP is first proposed by Hummon and Doreian.[1] The SPNP values of the link (C, H) is 6 because there are 6 paths that begin from A, B, C (A and B are C's ancestors) and end at H and K (K is H's descendant). These paths are A-C-H, A-C-H-K, B-C-H, B-C-H-K, C-H, and C-H-K.
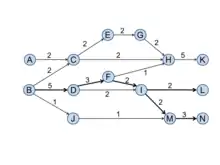
Path search
Based on the traversal counts, one can then search for the most significant path(s). There are several ways of finding them, including local, global, and key-route search.
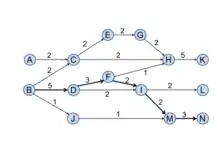
Local search
Local search is mentioned in Hummon and Doreian[1] as "priority first" search. This search process always chooses the next link(s) with the highest SPX as the outgoing link. It keeps tracking the most traversed link(s) thus obtains the main stream among all citation chains. Figure 4 shows the local main paths that are obtained based on SPC. Noticing that when the search reaches the node I, two outgoing links have the same SPC values thus producing two paths afterward.

Global search
Global search simply suggests the citation chain with the largest overall SPX. The concept of global search is similar to the critical path method in project scheduling. The global main paths of the sample citation network based on SPC is presented in Figure 5. The sum of all the SPC values in the path B-D-F-I-M-N is 15, which is the largest among all possible paths.
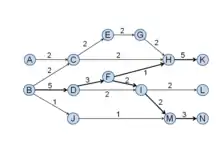
Key-route search
Key-route search is designed to avoid the problem of missing significant links in both the local and global search. The problem is in the local and global main paths shown above, in which one of the most important links (H, K) is not included in the main paths. As described in Liu and Lu (2012),[7] the approach searches main paths from the specified links (key-routes) thus guarantees the inclusion of the links. One can also specify multiple links to obtain multiple main paths. An additional advantage of the key-route approach is that one is able to control the detail of the main paths by varying the number of key-routes. The larger the number of key-route is specified, the more detail is revealed. When the number of key-route increases to a certain point the search returns the whole citation network. Figure 6 and 7 show the local key-route and global key-route main paths of the sample citation network. In both main paths the number of key-route is set to 1, i.e., doing the search base on only the top links. Since there are two top links (B, D) and (H, K), the resulting main paths include both of them.
The Variants
In addition to the key-route search approach, variations of the method include the approach that is aggregative and stochastic,[10] considers decay in knowledge diffusion,[8] etc.
Applications
The method has been applied to three types of documenting system that maintain the tradition of making references to the previous documents. They are the academic article, patent, and judicial documenting system.
Academic article
Academic citation databases such as Web of Science and Scopus include comprehensive digitized citation information. These information make it possible to apply main path analysis to examine the knowledge structure or trace the knowledge flow of any scientific fields. Some early applications explores the subject of centrality-productivity,[11] conflict resolution,[12] etc. More recent applications include fullerenes,[4] nanotubes,[4] data envelopment analysis,[2][13][14] supply chain management,[15] corporate social responsibility,[16] IT outsourcing,[17] medical tourism,[18] etc.
Patent
Patents referencing prior arts is a common practice. For example, each United States patent document includes a "References Cited" section that lists the prior arts of the patent. Patent databases such as Clarivate Analytics and Webpat provide digitized patent citation information. Verspagen (2007)[3] and Mina (2007)[19] are the two early works that apply main path analysis to the patent data.
Judicial document
In the common law system, a court decision document usually references previously published opinions for the purpose of justifying the current decision. These judicial references, or legal citations, can also be used to construct citation networks and then tracing the changes of legal opinions. Research opportunity in this area is wide open. Liu et al. (2014)[5] conducted an exploratory study on such type of application.
Software Implementation
Main path analysis is implemented in Pajek, a widely used social network analysis software written by Vladimir Batagelj and Andrej Mrvar of University of Ljubljana, Slovenia. To run main path analysis in Pajek, one needs to first prepare a citation network and have Pajek reads in the network. Next, in the Pajek main menu, computes the traversal counts of all links in the network applying one of the following command sequences (depending on the choice of traversal counts).
Network → Acyclic Network → Create Weighted Network + Vector → Traversal Weights → Search Path Link Count (SPC), or
Network → Acyclic Network → Create Weighted Network + Vector → Traversal Weights → Search Path Link Count (SPLC), or
Network → Acyclic Network → Create Weighted Network + Vector → Traversal Weights → Search Path Node Pairs (SPNP)
After traversal counts are computed, the following command sequences find the main paths.
For local main paths
Network → Acyclic Network → Create (Sub)Network → Main Paths → Local Search → Forward
For global main paths
Network → Acyclic Network → Create (Sub)Network → Main Paths → Global Search → Standard
For local key-route main paths
Network → Acyclic Network → Create (Sub)Network → Main Paths → Local Search → Key-Route
For global key-route main paths
Network → Acyclic Network → Create (Sub)Network → Main Paths → Global Search → Key-Route
In addition to key-route search, a more flexible search feature is added starting from Pajek version 5.03 (January 4, 2018). The new feature allows for local and global search passing through vertices defined by a cluster. The command sequences are as follows:
Network → Acyclic Network → Create (Sub)Network → Main Paths → Local Search → Key-Route → Through Vertices in Cluster
Network → Acyclic Network → Create (Sub)Network → Main Paths → Global Search → Key-Route → Through Vertices in Cluster
References
- 1 2 3 4 5 6 7 Hummon, Norman P.; Doreian, Patrick (1989). "Connectivity in a citation network: The development of DNA theory". Social Networks. 11 (1): 39–63. doi:10.1016/0378-8733(89)90017-8.
- 1 2 Liu, John S.; Lu, Louis Y.Y.; Lu, Wen-Min; Lin, Bruce J.Y. (2013). "Data envelopment analysis 1978–2010: A citation-based literature survey". Omega. 41 (1): 3–15. doi:10.1016/j.omega.2010.12.006.
- 1 2 Verspagen, Bart (2007-03-01). "Mapping technological trajectories as patent citation networks: a study on the history of fuel cell research". Advances in Complex Systems. 10 (1): 93–115. doi:10.1142/S0219525907000945. ISSN 0219-5259.
- 1 2 3 Lucio-Arias, Diana; Leydesdorff, Loet (2008-10-01). "Main-path analysis and path-dependent transitions in HistCite™-based historiograms". Journal of the American Society for Information Science and Technology. 59 (12): 1948–1962. doi:10.1002/asi.20903. ISSN 1532-2890.
- 1 2 Liu, John S.; Chen, Hsiao-Hui; Ho, Mei Hsiu-Ching; Li, Yu-Chen (2014-12-01). "Citations with different levels of relevancy: Tracing the main paths of legal opinions". Journal of the Association for Information Science and Technology. 65 (12): 2479–2488. doi:10.1002/asi.23135. ISSN 2330-1643.
- ↑ Liu, John S.; Lu, Louis Y. Y.; Ho, Mei Hsiu-Ching (2019-04-01). "A few notes on main path analysis". Scientometrics. 119 (1): 379–391. doi:10.1007/s11192-019-03034-x. ISSN 1588-2861.
- 1 2 Liu, John S.; Lu, Louis Y.Y. (2012-03-01). "An integrated approach for main path analysis: Development of the Hirsch index as an example". Journal of the American Society for Information Science and Technology. 63 (3): 528–542. doi:10.1002/asi.21692. ISSN 1532-2890.
- 1 2 Liu, John S.; Kuan, Chung-Huei (2016-02-01). "A new approach for main path analysis: Decay in knowledge diffusion". Journal of the Association for Information Science and Technology. 67 (2): 465–476. doi:10.1002/asi.23384. ISSN 2330-1643.
- ↑ Batagelj, V. (2003). Efficient algorithms for citation network analysis. arXiv preprint cs/0309023.
- ↑ Yeo, Woondong; Kim, Seonho; Lee, Jae-Min; Kang, Jaewoo (2014-01-01). "Aggregative and stochastic model of main path identification: a case study on graphene". Scientometrics. 98 (1): 633–655. doi:10.1007/s11192-013-1140-3. ISSN 0138-9130.
- ↑ Hummon, Norman P.; Doreian, Patrick; Freeman, Linton C. (2016-08-18). "Analyzing the Structure of the Centrality-Productivity Literature Created Between 1948 and 1979". Knowledge. 11 (4): 459–480. doi:10.1177/107554709001100405.
- ↑ Carley, Kathleen M.; Hummon, Norman P.; Harty, Martha (2016-08-17). "Scientific Influence". Knowledge. 14 (4): 417–447. doi:10.1177/107554709301400406.
- ↑ Liu, John S.; Lu, Louis Y.Y.; Lu, Wen-Min (2016). "Research fronts in data envelopment analysis". Omega. 58: 33–45. doi:10.1016/j.omega.2015.04.004.
- ↑ Liu, John S.; Lu, Louis Y.Y.; Lu, Wen-Min; Lin, Bruce J.Y. (2013). "A survey of DEA applications". Omega. 41 (5): 893–902. doi:10.1016/j.omega.2012.11.004.
- ↑ Claudia Colicchia; Fernanda Strozzi (2012-06-15). "Supply chain risk management: a new methodology for a systematic literature review". Supply Chain Management. 17 (4): 403–418. doi:10.1108/13598541211246558. ISSN 1359-8546.
- ↑ Lu, Louis Y.Y.; Liu, John S. (2014-03-01). "The Knowledge Diffusion Paths of Corporate Social Responsibility – From 1970 to 2011". Corporate Social Responsibility and Environmental Management. 21 (2): 113–128. doi:10.1002/csr.1309. ISSN 1535-3966.
- ↑ Liang, Huigang; Wang, Jian-Jun; Xue, Yajiong; Cui, Xiaocong (2016). "IT outsourcing research from 1992 to 2013: A literature review based on main path analysis". Information & Management. 53 (2): 227–251. doi:10.1016/j.im.2015.10.001.
- ↑ Chuang, Thomas C.; Liu, John S.; Lu, Louis Y.Y.; Lee, Yachi (2014). "The main paths of medical tourism: From transplantation to beautification". Tourism Management. 45: 49–58. doi:10.1016/j.tourman.2014.03.016.
- ↑ Mina, A.; Ramlogan, R.; Tampubolon, G.; Metcalfe, J.S. (2007). "Mapping evolutionary trajectories: Applications to the growth and transformation of medical knowledge". Research Policy. 36 (5): 789–806. doi:10.1016/j.respol.2006.12.007.
External links
- Pajek, a free social network analysis software.
- List of main path articles, this page contain a list of academic articles that introduce, explain, apply, modify, or extend the method originated in Hummon and Doreian.