Johannes Max Brückner
Born(1860-08-05)August 5, 1860
Hartau, Kingdom of Saxony
DiedNovember 1, 1934(1934-11-01) (aged 74)
Bautzen, Germany
EducationLeipzig University
Heidelberg University
Scientific career
Doctoral advisorFelix Klein
Wilhelm Scheibner
Brückner's photo of the final stellation of the icosahedron, a stellated polyhedron first studied by Brückner
Drawings of 4-polytopes in an essay from 1909

Johannes Max Brückner (5 August 1860 – 1 November 1934) was a German geometer, known for his collection of polyhedral models.

Education and career

Brückner was born in Hartau, in the Kingdom of Saxony, a town that is now part of Zittau, Germany.[1] He completed a Ph.D. at Leipzig University in 1886, supervised by Felix Klein and Wilhelm Scheibner, with a dissertation concerning conformal maps.[1][2] After teaching at a grammar school in Zwickau, he moved to the gymnasium in Bautzen.[1]

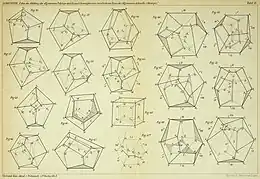
Brückner is known for making many geometric models, particularly of stellated and uniform polyhedra, which he documented in his book Vielecke und Vielflache: Theorie und Geschichte (Polygons and polyhedra: Theory and History, Leipzig: B. G. Teubner, 1900).[3][4] The shapes first studied in this book include the final stellation of the icosahedron and the compound of three octahedra, made famous by M. C. Escher's print Stars.[5] Joseph Malkevitch lists the publication of this book, which documented all that was known on polyhedra at the time, as one of 25 milestones in the history of polyhedra. Malkevitch writes that the book's "beautiful pictures of uniform polyhedra ... served as an inspiration to people later".[6]

Brückner died on November 1, 1934, in Bautzen.[1]

Honors and awards

Brückner was an invited speaker at the International Congress of Mathematicians in 1904, 1908, 1912, and 1928.[7] In 1930–1931 he donated his model collection to Heidelberg University,[1] and the university in turn gave him an honorary doctorate in 1931.[1][2]

Bibliography

  • Die Elemente der vierdimensionalen Geometrie mit besonderer Berücksichtigung der Polytope, Jahresbericht des Vereins für Naturkunde zu Zwickau 1893
  • Vielecke und Vielflache – Theorie und Geschichte, Teubner, Leipzig, 1900
  • Über die gleicheckig-gleichflächigen, diskontinuierlichen und nichtkonvexen Polyeder. dans: Abhandlungen der kaiserlichen leopoldinisch-carolinischen deutschen Akademie der Naturforscher, vol. 86, p. 1–348, Halle 1906.
  • Ueber die Ableitung der allgemeinen Polytope und die nach Isomorphismus verschiedenen Typen der allgemeinen Achtzelle (Oktatope), Verhandelingen der Koninklijke Akademie van Wetenschappen, Amsterdam 1909

References

  1. 1 2 3 4 5 6 Steck, Max (1955), "Brueckner, Johannes Max", Neue Deutsche Biographie (in German), vol. 2, Berlin: Duncker & Humblot, pp. 657–658; (full text online)
  2. 1 2 Max Brückner at the Mathematics Genealogy Project
  3. ↑ Vielecke und Vielflache on Internet Archive, accessed 2015-12-01.
  4. ↑ Gabriel, J. François (1997), "Max Brückner (1860–1934) and his paper model collection", Beyond the Cube: The Architecture of Space Frames and Polyhedra, John Wiley & Sons, p. 28, ISBN 9780471122616.
  5. ↑ Coxeter, H. S. M. (1985), "A special book review: M. C. Escher: His life and complete graphic work", The Mathematical Intelligencer, 7 (1): 59–69, doi:10.1007/BF03023010, S2CID 189887063. Coxeter's analysis of Stars is on pp. 61–62.
  6. ↑ Malkevitch, Joseph (2013), "Milestones in the History of Polyhedra", in Senechal, Marjorie (ed.), Shaping Space: Exploring Polyhedra in Nature, Art, and the Geometrical Imagination, Springer, pp. 53–63, doi:10.1007/978-0-387-92714-5_4, ISBN 978-0-387-92713-8.
  7. ↑ ICM Plenary and Invited Speakers since 1897, International Mathematical Union, retrieved 2015-10-01.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.