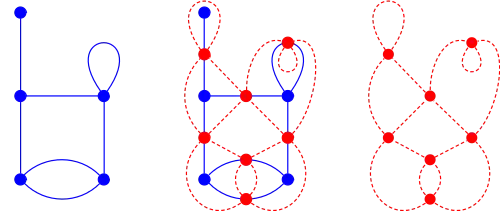
A plane graph (in blue) and its medial graph (in red).

In the mathematical discipline of graph theory, the medial graph of plane graph G is another graph M(G) that represents the adjacencies between edges in the faces of G. Medial graphs were introduced in 1922 by Ernst Steinitz to study combinatorial properties of convex polyhedra,[1] although the inverse construction was already used by Peter Tait in 1877 in his foundational study of knots and links.[2][3]

Formal definition

Given a connected plane graph G, its medial graph M(G) has

  • a vertex for each edge of G and
  • an edge between two vertices for each face of G in which their corresponding edges occur consecutively.

The medial graph of a disconnected graph is the disjoint union of the medial graphs of each connected component. The definition of medial graph also extends without modification to graph embeddings on surfaces of higher genus.

Properties

The two red graphs are both medial graphs of the blue graph, but they are not isomorphic.
  • The medial graph of any plane graph is a 4-regular plane graph.
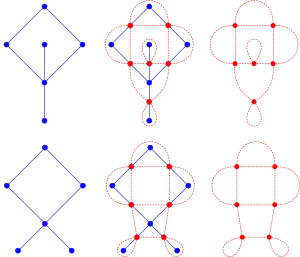
  • For any plane graph G, the medial graph of G and the medial graph of the dual graph of G are isomorphic. Conversely, for any 4-regular plane graph H, the only two plane graphs with medial graph H are dual to each other.[4]
  • Since the medial graph depends on a particular embedding, the medial graph of a planar graph is not unique; the same planar graph can have non-isomorphic medial graphs. In the picture, the red graphs are not isomorphic because the two vertices with self loops share an edge in one graph but not in the other.
  • Every 4-regular plane graph is the medial graph of some plane graph. For a connected 4-regular plane graph H, a planar graph G with H as its medial graph can be constructed as follows. Color the faces of H with just two colors, which is possible since H is Eulerian (and thus the dual graph of H is bipartite). The vertices in G correspond to the faces of a single color in H. These vertices are connected by an edge for each vertex shared by their corresponding faces in H. Note that performing this construction using the faces of the other color as the vertices produces the dual graph of G.
  • The medial graph of a 3-regular plane graph coincides with its line graph. However, this is not true for medial graphs of plane graphs that have vertices of degree greater than three.

Applications

For a plane graph G, twice the evaluation of the Tutte polynomial at the point (3,3) equals the sum over weighted Eulerian orientations in the medial graph of G, where the weight of an orientation is 2 to the number of saddle vertices of the orientation (that is, the number of vertices with incident edges cyclically ordered "in, out, in out").[5] Since the Tutte polynomial is invariant under embeddings, this result shows that every medial graph has the same sum of these weighted Eulerian orientations.

Directed medial graph

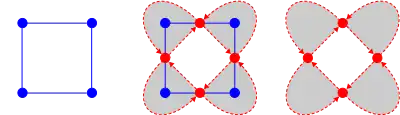
A plane graph (in blue) and its directed medial graph (in red).

The medial graph definition can be extended to include an orientation. First, the faces of the medial graph are colored black if they contain a vertex of the original graph and white otherwise. This coloring causes each edge of the medial graph to be bordered by one black face and one white face. Then each edge is oriented so that the black face is on its left.

A plane graph and its dual do not have the same directed medial graph; their directed medial graphs are the transpose of each other.

Using the directed medial graph, one can effectively generalize the result on evaluations of the Tutte polynomial at (3,3). For a plane graph G, n times the evaluation of the Tutte polynomial at the point (n+1,n+1) equals the weighted sum over all edge colorings using n colors in the directed medial graph of G so that each (possibly empty) set of monochromatic edges forms a directed Eulerian graph, where the weight of a directed Eulerian orientation is 2 to the number of monochromatic vertices.[6]

See also

References

  1. ↑ Steinitz, Ernst (1922), "Polyeder und Raumeinteilungen", Encyclopädie der mathematischen Wissenschaften, Band 3 (Geometries), pp. 1–139
  2. ↑ Tait, Peter G. (1876–1877). "On Knots I". Transactions of the Royal Society of Edinburgh. 28: 145–190. doi:10.1017/S0080456800090633. S2CID 171186257. Revised May 11, 1877.
  3. ↑ Tait, Peter G. (1876–1877). "On Links (Abstract)". Proceedings of the Royal Society of Edinburgh. 9 (98): 321–332. doi:10.1017/S0370164600032363.
  4. ↑ Gross, Jonathan L.; Yellen, Jay, eds. (2003). Handbook of Graph Theory. CRC Press. p. 724. ISBN 978-1584880905.
  5. ↑ Las Vergnas, Michel (1988), "On the evaluation at (3, 3) of the Tutte polynomial of a graph", Journal of Combinatorial Theory, Series B, 35 (3): 367–372, doi:10.1016/0095-8956(88)90079-2, ISSN 0095-8956
  6. ↑ Ellis-Monaghan, Joanna A. (2004). "Identities for circuit partition polynomials, with applications to the Tutte polynomial". Advances in Applied Mathematics. 32 (1–2): 188–197. doi:10.1016/S0196-8858(03)00079-4. ISSN 0196-8858.

Further reading

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.