Suppose that ${\displaystyle ({\mathcal {C}},\otimes ,I)}$ and ${\displaystyle ({\mathcal {D}},\bullet ,J)}$ are two monoidal categories and

${\displaystyle (F,m):({\mathcal {C}},\otimes ,I)\to ({\mathcal {D}},\bullet ,J)}$ and ${\displaystyle (G,n):({\mathcal {C}},\otimes ,I)\to ({\mathcal {D}},\bullet ,J)}$

are two lax monoidal functors between those categories.

A monoidal natural transformation

${\displaystyle \theta$ :(F,m)\to (G,n)}

between those functors is a natural transformation ${\displaystyle \theta :F\to G}$ between the underlying functors such that the diagrams

           and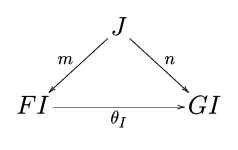         

commute for every objects ${\displaystyle A}$ and ${\displaystyle B}$ of ${\displaystyle {\mathcal {C}}}$ (see Definition 11 in ^[1]).

A symmetric monoidal natural transformation is a monoidal natural transformation between symmetric monoidal functors.

References