The 2- and 3-fold covers of 7 points in the plane with respect to a particular scale parameter.

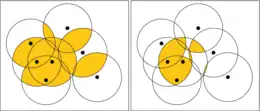
The multicover bifiltration is a two-parameter sequence of nested topological spaces derived from the covering of a finite set in a metric space by growing metric balls. It is a multidimensional extension of the offset filtration that captures density information about the underlying data set by filtering the points of the offsets at each index according to how many balls cover each point.^[1] The multicover bifiltration has been an object of study within multidimensional persistent homology and topological data analysis.^{[2][3][4][5][6][7]}

Definition

Following the notation of Corbet et al. (2022), given a finite set ${\displaystyle A\subset \mathbb {R} ^{d}}$, the multicover bifiltration on ${\displaystyle A}$ is a two-parameter filtration indexed by ${\displaystyle \mathbb {R} \times \mathbb {N} ^{\text{op}}}$ defined index-wise as ${\displaystyle \operatorname {Cov} _{r,k}:=\{b\in \mathbb {R} ^{d}:||b-a||\leq r{\text{ for at least }}k{\text{ points }}a\in A\}}$, where ${\displaystyle \mathbb {N} }$ denotes the non-negative integers.^[8] Note that when ${\displaystyle k=1}$ is fixed we recover the Offset Filtration.

Properties

The multicover bifiltration admits a polynomially-sized simplicial model that is topologically equivalent, called the "rhomboid bifiltration."^[8] The rhomboid bifiltration is an extension of the rhomboid tiling introduced by Edelsbrunner and Osang in 2021 for computing the persistent homology of the multicover bifiltration along one axis of the indexing set.^[2] The rhomboid bifiltration on a set of ${\displaystyle n}$ points in Euclidean space can be computed in time ${\displaystyle O(n^{5})}$.^[8]

An example of the rhomboid tiling on a set of five points.

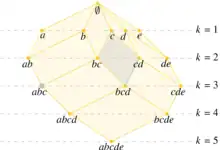
The multicover bifiltration is also topologically equivalent to a multicover nerve construction due to Sheehy called the subdivision-Čech bifiltration, which considers the barycentric subdivision on the nerve of the offsets.^[9] In particular, the subdivision-Čech and multicover bifiltrations are weakly equivalent, and hence have isomorphic homology modules in all dimensions.^[4] However, the subdivision-Čech bifiltration has an exponential number of simplices in the size of the data set, and hence is not amenable to efficient direct computations.^[8]

References