The term neopolarogram refers to mathematical derivatives of polarograms or cyclic voltammograms that in effect deconvolute diffusion and electrochemical kinetics. This is achieved by analog or digital implementations of fractional calculus.[1] The implementation of fractional derivative calculations by means of numerical methods is straight forward. The G1- (Grünwald–Letnikov derivative) and the RL0-algorithms (Riemann–Liouville integral) are recursive methods to implement a numerical calculation of fractional differintegrals. Yet differintegrals are faster to compute in discrete fourier space using FFT.[2]
Applications
The graphs below show the behaviour of fractional derivatives calculated by different algorithms for ferrocene in acetonitrile at 100mV/s, the reference electrode is 0.1M Ag+/Ag in acetonitrile (+0.04V vs. Fc[3]).
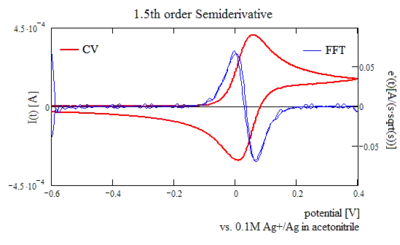
1st derivative of the "Semiderivative" or 1.5th order derivative in voltammetry
1.5th order derivative of a voltammogram hits the abscissa exactly at the point where the formal potential of the electrode reaction is found.
|
|
| Typical 1.5th order semiderivative for a reversible reaction, ferrocene has a formal potential of 40mV vs. ATE1.[3] |
|---|
"Semiderivative" or numerical Grünberg-Letnikov derivative in voltammetry
The G1 algorithm produces a numerical derivative that has the shape of a bell curve, this derivative obeys to certain laws, for example the G1 derivative of a cyclic voltammogram is mirrored at the abscissa as long as the electrochemical reaction is diffusion controlled, the planar diffusion approximation can be applied to the electrode geometry[4] and ohmic drop distortion is minimal. The FWHM of the curve is approximately 100 mV for a system that behaves in the described manner. The maximum is found at the value of the formal potential, this is equivalent to the 1.5th order semiderivative hitting the abscissa at this potential. Moreover the semiderivative scales linearly with the scanrate, while the current scales linearly with the square root of the scanrate (Randles–Sevcik equation). Plotting the semiderivatives produced at different scanrates gives a family of curves that are linearly related by the scanrate quotient in an ideal system.
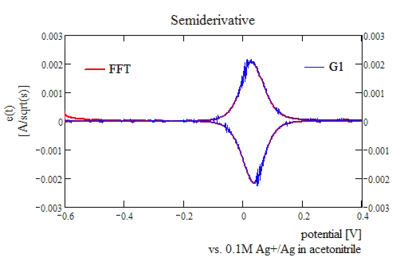 Typical semiderivative for a reversible reaction, recursive algorithms and FFT methods yield equivalent results. |
| Typical semiderivative for a reversible reaction, recursive algorithms and FFT methods yield equivalent results. |
|---|
"Semiintegral" or numerical Riemann-Liouville integral in voltammetry
The shape of the semiintegral can be used as an easy method to measure the amount of ohmic drop of an electrochemical cell in cyclic voltammetry. Essentially the semiintegral of a cyclic voltammogram at a planar electrode (an electrode that obeys to the rules of planar diffusion) has the shape of a sigmoid while the original data is gauss-sigmoid convoluted. This enables the operator to optimize parameters necessary for positive feedback compensation in an easy manner.[5] If ohmic drop distortion is present the two sigmoids for the forward and the backward scan are far away from congruence, the ohmic drop can be calculated from the deviation from congruence in these cases. In the example shown slight distortion is present, yet this does not have adverse effects on data quality.
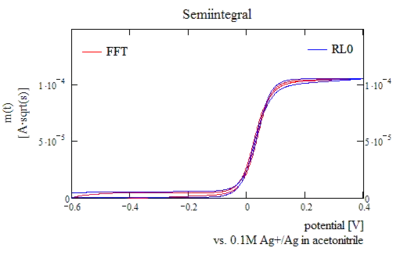 Typical semiintegral for a reversible reaction, recursive algorithms and FFT methods yield slightly different results due to non-perfect periodicity of cyclic voltammetry data. |
| Typical semiintegral for a reversible reaction, recursive algorithms and FFT methods yield slightly different
results due to non-perfect periodicity of cyclic voltammetry data. |
|---|
Merits of FFT techniques
The implementation differintegral calculation using fast fourier transform has certain benefits because it is easily combined with low pass quadratic filtering methods.[6] This is very useful when cyclic voltammograms are recorded in high resistivity solvents like tetrahydrofuran or toluene, where feedback oscillations are a frequent problem.
References
- ↑ Keith Oldham, Jerome Spanier; The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order (Dover Books on Mathematics)
- ↑ Jun-Sheng Yu, Zu-Xun Zhanga; "Differentiation, semidifferentiation and semi-integration of a digital signals based on Fourier transformations"; Journal of Electroanalytical Chemistry; Volume 403, Issues 1-2, 21 February 1996, Pages 1-9; doi:10.1016/0022-0728(95)04328-4
- 1 2 3 Vitaly V. Pavlishchuk and Anthony W. Addison; "Conversion constants for redox potentials measured versus different reference electrodes in acetonitrile solutions at 25 °C"; Inorganica Chimica Acta Volume 298, Issue 1, 30 January 2000, Pages 97–102; doi:10.1016/S0020-1693(99)00407-7
- ↑ Masashi Goto, Keith B. Oldham; "Semiintegral electroanalysis. Shapes of neopolarograms"; Anal. Chem., 1973, 45 (12), pp 2043–2050; doi:10.1021/ac60334a027
- ↑ Alan M. Bond, Keith B. Oldham, and Graeme A. Snook; "Use of the Ferrocene Oxidation Process To Provide Both Reference Electrode Potential Calibration and a Simple Measurement (via Semiintegration) of the Uncompensated Resistance in Cyclic Voltammetric Studies in High-Resistance Organic Solvents"; Anal. Chem., 2000, 72 (15), pp 3492–3496 doi:10.1021/ac000020j
- ↑ Eric E. Aubanela, Janice C. Mylanda, Keith B. Oldham and Cynthia G. Zoskia; "Fourier smoothing of electrochemical data without the fast fourier transform"; Journal of Electroanalytical Chemistry and Interfacial Electrochemistry; Volume 184, Issue 2, 25 March 1985, Pages 239-255; doi:10.1016/0368-1874(85)85531-3