 | |
| Classification | Baryon |
|---|---|
| Composition | 1 up quark, 2 down quarks |
| Statistics | Fermionic |
| Family | Hadron |
| Interactions | Gravity, weak, strong, electromagnetic |
| Symbol | n , n0 , N0 |
| Antiparticle | Antineutron |
| Theorized | Ernest Rutherford[1] (1920) |
| Discovered | James Chadwick[2] (1932) |
| Mass | 1.67492749804(95)×10−27 kg[3] 939.56542052(54) MeV/c2[3] 1.00866491588(49) Da[4] |
| Mean lifetime | 879.4(6) s (free)[5] |
| Electric charge | 0 e (−2±8)×10−22 e (experimental limits)[6] |
| Electric dipole moment | < 1.8×10−26 e⋅cm (experimental upper limit) |
| Electric polarizability | 1.16(15)×10−3 fm3 |
| Magnetic moment | −0.96623650(23)×10−26 J·T−1[4] −1.04187563(25)×10−3 μB[4] −1.91304273(45) μN[4] |
| Magnetic polarizability | 3.7(20)×10−4 fm3 |
| Spin | 1/2 ħ |
| Isospin | −1/2 |
| Parity | +1 |
| Condensed | I(JP) = 1/2(1/2+) |
The neutron is a subatomic particle, symbol
n
or
n0
, which has a neutral (not positive or negative) charge, and a mass slightly greater than that of a proton. Protons and neutrons constitute the nuclei of atoms. Since protons and neutrons behave similarly within the nucleus, they are both referred to as nucleons. Nucleons have a mass of approximately one atomic mass unit, or dalton, symbol Da. Their properties and interactions are described by nuclear physics. Protons and neutrons are not elementary particles; each is composed of three quarks.
The chemical properties of an atom are mostly determined by the configuration of electrons that orbit the atom's heavy nucleus. The electron configuration is determined by the charge of the nucleus, which is determined by the number of protons, or atomic number. The number of neutrons is the neutron number. Neutrons do not affect the electron configuration.
Atoms of a chemical element that differ only in neutron number are called isotopes. For example, carbon, with atomic number 6, has an abundant isotope carbon-12 with 6 neutrons and a rare isotope carbon-13 with 7 neutrons. Some elements occur in nature with only one stable isotope, such as fluorine. Other elements occur with many stable isotopes, such as tin with ten stable isotopes, or with no stable isotope, such as technetium.
The properties of an atomic nucleus depend on both atomic and neutron numbers. With their positive charge, the protons within the nucleus are repelled by the long-range electromagnetic force, but the much stronger, but short-range, nuclear force binds the nucleons closely together. Neutrons are required for the stability of nuclei, with the exception of the single-proton hydrogen nucleus. Neutrons are produced copiously in nuclear fission and fusion. They are a primary contributor to the nucleosynthesis of chemical elements within stars through fission, fusion, and neutron capture processes.
The neutron is essential to the production of nuclear power. In the decade after the neutron was discovered by James Chadwick in 1932, neutrons were used to induce many different types of nuclear transmutations. With the discovery of nuclear fission in 1938, it was quickly realized that, if a fission event produced neutrons, each of these neutrons might cause further fission events, in a cascade known as a nuclear chain reaction. These events and findings led to the first self-sustaining nuclear reactor (Chicago Pile-1, 1942) and the first nuclear weapon (Trinity, 1945).
Dedicated neutron sources like neutron generators, research reactors and spallation sources produce free neutrons for use in irradiation and in neutron scattering experiments. A free neutron spontaneously decays to a proton, an electron, and an antineutrino, with a mean lifetime of about 15 minutes. Free neutrons do not directly ionize atoms, but they do indirectly cause ionizing radiation, so they can be a biological hazard, depending on dose. A small natural "neutron background" flux of free neutrons exists on Earth, caused by cosmic ray showers, and by the natural radioactivity of spontaneously fissionable elements in the Earth's crust.
Neutrons in an atomic nucleus
| Nuclear physics |
|---|
 |
|
An atomic nucleus is formed by a number of protons, Z (the atomic number), and a number of neutrons, N (the neutron number), bound together by the nuclear force. Protons and neutrons each have a mass of approximately one dalton. The atomic number determines the chemical properties of the atom, and the neutron number determines the isotope or nuclide.[7] The terms isotope and nuclide are often used synonymously, but they refer to chemical and nuclear properties, respectively. Isotopes are nuclides with the same atomic number, but different neutron number. Nuclides with the same neutron number, but different atomic number, are called isotones. The atomic mass number, A, is equal to the sum of atomic and neutron numbers. Nuclides with the same atomic mass number, but different atomic and neutron numbers, are called isobars. The mass of a nucleus is always slightly less than the sum of its proton and neutron masses: the difference in mass represents the mass equivalent to nuclear binding energy, the energy which would need to be added to take the nucleus apart.[8]: 822
The nucleus of the most common isotope of the hydrogen atom (with the chemical symbol 1H) is a lone proton. The nuclei of the heavy hydrogen isotopes deuterium (D or 2H) and tritium (T or 3H) contain one proton bound to one and two neutrons, respectively. All other types of atomic nuclei are composed of two or more protons and various numbers of neutrons. The most common nuclide of the common chemical element lead, 208Pb, has 82 protons and 126 neutrons, for example. The table of nuclides comprises all the known nuclides. Even though it is not a chemical element, the neutron is included in this table.[9]
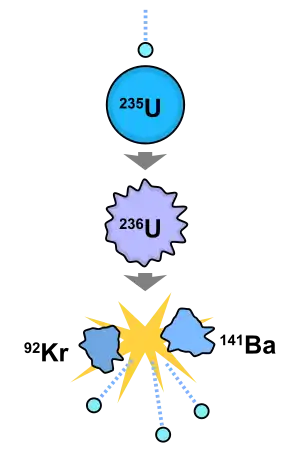
Protons and neutrons behave almost identically under the influence of the nuclear force within the nucleus. They are therefore both referred to collectively as nucleons.[10] The concept of isospin, in which the proton and neutron are viewed as two quantum states of the same particle, is used to model the interactions of nucleons by the nuclear or weak forces. Because of the strength of the nuclear force at short distances, the binding energy of nucleons is more than seven orders of magnitude larger than the electromagnetic energy binding electrons in atoms. Nuclear reactions (such as nuclear fission) therefore have an energy density that is more than ten million times that of chemical reactions. Because of the mass–energy equivalence, nuclear binding energies reduce the mass of nuclei. Ultimately, the ability of the nuclear force to store energy arising from the electromagnetic repulsion of nuclear components is the basis for most of the energy that makes nuclear reactors or bombs possible. In nuclear fission, the absorption of a neutron by a heavy nuclide (e.g., uranium-235) causes the nuclide to become unstable and break into light nuclides and additional neutrons. The positively charged light nuclides then repel, releasing electromagnetic potential energy.
Beta decay
Neutrons and protons within a nucleus behave similarly and can exchange their identities by similar reactions. These reactions are a form of radioactive decay known as beta decay. Beta decay, in which neutrons decay to protons, or vice versa, is governed by the weak force, and it requires the emission or absorption of electrons and neutrinos, or their antiparticles. The neutron and proton decay reactions are:
n0
→
p+
+
e−
+
ν
e
where
p+
,
e−
, and
ν
e denote the proton, electron and electron anti-neutrino decay products,[11] and
p+
→
n0
+
e+
+
ν
e
where
n0
,
e+
, and
ν
e denote the neutron, positron and electron neutrino decay products.
The electron and positron produced in these reactions are historically known as beta particles, denoted β− or β+ respectively, lending the name to the decay process. In these reactions, the original particle is not composed of the product particles; rather, the product particles are created at the instant of the reaction.
The "free" neutron
"Free" neutrons or protons are nucleons that exist independently, free of any nucleus.
The free neutron has a mass of 939565413.3 eV/c2, or 1.674927471×10−27 kg, or 1.00866491588 Da.[4] The neutron has a mean square radius of about 0.8×10−15 m, or 0.8 fm,[12] and it is a spin-½ fermion.[13] The neutron has no measurable electric charge. With its positive electric charge, the proton is directly influenced by electric fields, whereas the neutron is unaffected by electric fields. But the neutron has a magnetic moment, so the neutron is influenced by magnetic fields. The specific properties of the neutron are described below in the Intrinsic properties section.
Outside the nucleus, free neutrons are unstable and have a mean lifetime of 879.6±0.8 s (about 14 minutes, 40 seconds) by beta decay; therefore the half-life for this process (which differs from the mean lifetime by a factor of ln(2) = 0.693) is 610.1±0.7 s (about 10 minutes, 10 seconds).[14][15] This decay, which produces a proton, an electron and electron anti-neutrino, is possible because the mass of the neutron is slightly greater than that of the proton. By the mass-energy equivalence, when a neutron decays to a proton this way, a lower energy state is attained.
For the free neutron the decay energy for this process (based on the masses of the neutron, proton, and electron) is 0.782343 MeV. By comparison the mass energy of the neutron is 939.6 MeV. The maximal energy of the beta decay electron (in the process wherein the neutrino receives a vanishingly small amount of kinetic energy) has been measured at 0.782±0.013 MeV.[16] The latter number is not well-enough measured to determine the comparatively tiny rest mass of the neutrino (which must in theory be subtracted from the maximal electron kinetic energy). The neutrino mass is better constrained by many other methods.
The decay of a free proton to a more massive neutron is energetically disallowed. A high-energy collision of a proton and an electron or neutrino can result in a neutron, however.
A small fraction (about one in 1000) of free neutrons decay with the same products, but add an extra particle in the form of an emitted gamma ray:
n0
→
p+
+
e−
+
ν
e +
γ
This gamma ray may be thought of as an "internal bremsstrahlung" that arises from the electromagnetic interaction of the emitted beta particle with the proton. Internal bremsstrahlung gamma ray production is also a minor feature of beta decays of bound neutrons (as discussed below).

β−
radiation, the emission of a fast electron from the nucleus (the accompanying antineutrino is omitted). In the Rutherford model for the nucleus, red spheres were protons with positive charge and blue spheres were protons tightly bound to an electron with no net charge.
The inset shows beta decay of a free neutron as it is understood today; an electron and antineutrino are created in this process.
A very small minority of neutron decays (about four per million) are so-called "two-body (neutron) decays", in which a proton, electron and antineutrino are produced as usual, but the electron fails to gain the 13.6 eV necessary energy to escape the proton (the ionization energy of hydrogen), and therefore simply remains bound to it, forming a neutral hydrogen atom (one of the "two bodies"). In this type of free neutron decay, almost all of the neutron decay energy is carried off by the antineutrino (the other "body"). (The hydrogen atom recoils with a speed of only about (decay energy)/(hydrogen rest energy) times the speed of light, or 250 km/s.)
Neutrons and protons bound in a nucleus
Neutrons are a necessary constituent of any atomic nucleus that contains more than one proton. As a result of their positive charges, interacting protons have a mutual electromagnetic repulsion that is stronger than their attractive nuclear interaction, so proton-only nuclei are unstable (see diproton and neutron–proton ratio).[17] Neutrons bind with protons and one another in the nucleus via the nuclear force, effectively moderating the repulsive forces between the protons and stabilizing the nucleus.
While a free neutron has a half life of about 10.2 min and a free proton is stable, within nuclei neutrons are often stable and protons are sometimes unstable. When bound within a nucleus, nucleons can decay by the beta decay process. The neutrons and protons in a nucleus form a quantum mechanical system according to the nuclear shell model. Protons and neutrons of a nuclide are organized into discrete hierarchical energy levels with unique quantum numbers. Nucleon decay within a nucleus can occur if allowed by basic energy conservation and quantum mechanical constraints. The decay products, that is, the emitted particles, carry away the energy excess as a nucleon falls from one quantum state to one with less energy, while the neutron (or proton) changes to a proton (or neutron).
For a neutron to decay, the resulting proton requires an available state at lower energy than the initial neutron state. In stable nuclei the possible lower energy states are all filled, meaning each state is occupied by a pair of protons, one with spin up, another with spin down. When all available proton states are filled, the Pauli exclusion principle disallows the decay of a neutron to a proton within stable nuclei. The situation is similar to electrons of an atom, where electrons that occupy distinct atomic orbitals are prevented by the exclusion principle from decaying to lower, already-filled, energy states, with the emission of a photon. The stability of nuclei and nuclide radioactivity are consequences of these constraints.
One example of the decay of a neutron within a nuclide is the carbon isotope carbon-14, which has 6 protons and 8 neutrons. With its excess of neutrons, this isotope decays by beta decay to nitrogen-14 (7 protons, 7 neutrons) with a half-life of about 5,730 years. The decay emits an electron and an electron anti-neutrino. Nitrogen-14 is stable, since none of its protons or neutrons have available quantum states of lesser energy.
The transformation of a proton to a neutron inside of a nucleus is also possible through electron capture:
p+
+
e−
→
n0
+
ν
e
Positron capture by neutrons in nuclei that contain an excess of neutrons is also possible, but is hindered because positrons are both relatively rare in ordinary matter and quickly annihilate when they encounter electrons (which are much less rare) and in any case are repelled by the positive nucleus. Similar, but far more rare, reactions involve the capture of a neutrino by a nucleon in inverse beta decay.
Competition of beta decay types
Three types of beta decay in competition are illustrated by the single isotope copper-64 (29 protons, 35 neutrons), which has a half-life of about 12.7 hours. This isotope has one unpaired proton and one unpaired neutron, so either the proton or the neutron can decay. This particular nuclide is almost equally likely to undergo proton decay (by positron emission, 18% or by electron capture, 43%; both forming 64
Ni
) or neutron decay (by electron emission, 39%; forming 64
Zn
).
The neutron in elementary particle physics - the Standard Model
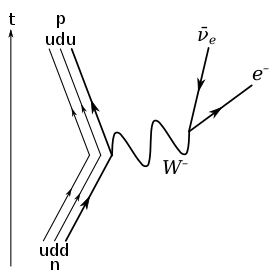
β−
decay of a neutron into a proton, electron, and electron antineutrino via an intermediate heavy
W−
boson.

β+
decay of a proton into a neutron, positron, and electron neutrino via an intermediate heavy
W+
boson.
Within the theoretical framework of Standard Model for particle physics, a neutron comprises two down quarks with charge −1/3e and one up quark with charge +2/3e.. The neutron is therefore a composite particle classified as a hadron. The neutron is also classified as a baryon, because it is composed of three valence quarks.[18] The finite size of the neutron and its magnetic moment both indicate that the neutron is a composite, rather than elementary, particle.
The quarks of the neutron are held together by the strong force, mediated by gluons.[19] The nuclear force results from secondary effects of the more fundamental strong force.
The only possible decay mode for the neutron that conserves baryon number is for one of the neutron's quarks to change flavour via the weak interaction. The decay of one of the neutron's down quarks into a lighter up quark can be achieved by the emission of a W boson. By this process, the Standard Model description of beta decay, the neutron decays into a proton (which contains one down and two up quarks), an electron, and an electron antineutrino.
The decay of the proton to a neutron occurs similarly through the weak force. The decay of one of the proton's up quarks into a down quark can be achieved by the emission of a W boson. The proton decays into a neutron, a positron, and an electron neutrino. This reaction can only occur within an atomic nucleus which has a quantum state at lower energy available for the created neutron.
Discovery
The story of the discovery of the neutron and its properties is central to the extraordinary developments in atomic physics that occurred in the first half of the 20th century, leading ultimately to the atomic bomb in 1945. In the 1911 Rutherford model, the atom consisted of a small positively charged massive nucleus surrounded by a much larger cloud of negatively charged electrons. In 1920, Ernest Rutherford suggested that the nucleus consisted of positive protons and neutrally charged particles, suggested to be a proton and an electron bound in some way.[20] Electrons were assumed to reside within the nucleus because it was known that beta radiation consisted of electrons emitted from the nucleus.[20] About the time Rutherford suggested the neutral proton-electron composite, several other publications appeared making similar suggestions, and in 1921 the American chemist W. D. Harkins first named the hypothetical particle a "neutron".[21][22] The name derives from the Latin root for neutralis (neuter) and the Greek suffix -on (a suffix used in the names of subatomic particles, i.e. electron and proton).[23][24] References to the word neutron in connection with the atom can be found in the literature as early as 1899, however.[22]
Throughout the 1920s, physicists assumed that the atomic nucleus was composed of protons and "nuclear electrons",[25][26] but this raised obvious problems. It was difficult to reconcile the proton–electron model of the nucleus with the Heisenberg uncertainty relation of quantum mechanics.[27][28] The Klein paradox,[29] discovered by Oskar Klein in 1928, presented further quantum mechanical objections to the notion of an electron confined within a nucleus.[27] Observed properties of atoms and molecules were inconsistent with the nuclear spin expected from the proton–electron hypothesis. Both protons and electrons carry an intrinsic spin of 1/2ħ. Isotopes of the same species (i.e. having the same number of protons) can have both integer or fractional spin, i.e. the neutron spin must be also fractional (1/2ħ). But there is no way to arrange the spins of an electron and a proton (supposed to bond to form a neutron) to get the fractional spin of a neutron.
In 1931, Walther Bothe and Herbert Becker found that if alpha particle radiation from polonium fell on beryllium, boron, or lithium, an unusually penetrating radiation was produced. The radiation was not influenced by an electric field, so Bothe and Becker assumed it was gamma radiation.[30][31] The following year Irène Joliot-Curie and Frédéric Joliot-Curie in Paris showed that if this "gamma" radiation fell on paraffin, or any other hydrogen-containing compound, it ejected protons of very high energy.[32] Neither Rutherford nor James Chadwick at the Cavendish Laboratory in Cambridge were convinced by the gamma ray interpretation.[33] Chadwick quickly performed a series of experiments that showed that the new radiation consisted of uncharged particles with about the same mass as the proton.[34][35][36] These properties matched Rutherford's hypothesized neutron. Chadwick won the 1935 Nobel Prize in Physics for this discovery.[2]

Models for an atomic nucleus consisting of protons and neutrons were quickly developed by Werner Heisenberg[37][38][39] and others.[40][41] The proton–neutron model explained the puzzle of nuclear spins. The origins of beta radiation were explained by Enrico Fermi in 1934 by the process of beta decay, in which the neutron decays to a proton by creating an electron and a (at the time undiscovered) neutrino.[42] In 1935, Chadwick and his doctoral student Maurice Goldhaber reported the first accurate measurement of the mass of the neutron.[43][44]
By 1934, Fermi had bombarded heavier elements with neutrons to induce radioactivity in elements of high atomic number. In 1938, Fermi received the Nobel Prize in Physics "for his demonstrations of the existence of new radioactive elements produced by neutron irradiation, and for his related discovery of nuclear reactions brought about by slow neutrons".[45] In December 1938 Otto Hahn, Lise Meitner, and Fritz Strassmann discovered nuclear fission, or the fractionation of uranium nuclei into lighter elements, induced by neutron bombardment.[46][47][48][49] In 1945 Hahn received the 1944 Nobel Prize in Chemistry "for his discovery of the fission of heavy atomic nuclei".[50][51][52]
The discovery of nuclear fission would lead to the development of nuclear power and the atomic bomb by the end of World War II. It was quickly realized that, if a fission event produced neutrons, each of these neutrons might cause further fission events, in a cascade known as a nuclear chain reaction.[7] These events and findings led Fermi to construct the Chicago Pile-1 at the University of Chicago in 1942, the first self-sustaining nuclear reactor. Just three years later the Manhattan Project was able to test the first atomic bomb, the Trinity nuclear test in July 1945.
Intrinsic properties
Mass
The mass of a neutron cannot be directly determined by mass spectrometry since it has no electric charge. But since the masses of a proton and of a deuteron can be measured with a mass spectrometer, the mass of a neutron can be deduced by subtracting proton mass from deuteron mass, with the difference being the mass of the neutron plus the binding energy of deuterium (expressed as a positive emitted energy). The latter can be directly measured by measuring the energy () of the single 2.224 MeV gamma photon emitted when a deuteron is formed by a proton capturing a neutron (this is exothermic and happens with zero-energy neutrons). The small recoil kinetic energy () of the deuteron (about 0.06% of the total energy) must also be accounted for.
The energy of the gamma ray can be measured to high precision by X-ray diffraction techniques, as was first done by Bell and Elliot in 1948. The best modern (1986) values for neutron mass by this technique are provided by Greene, et al.[53] These give a neutron mass of:
- mneutron = 1.008644904(14) Da
The value for the neutron mass in MeV is less accurately known, due to less accuracy in the known conversion of Da to MeV/c2:[54]
- mneutron = 939.56563(28) MeV/c2.
Another method to determine the mass of a neutron starts from the beta decay of the neutron, when the momenta of the resulting proton and electron are measured.
Spin
The neutron is a spin 1/2 particle, that is, it is a fermion with intrinsic angular momentum equal to 1/2 ħ, where ħ is the reduced Planck constant. For many years after the discovery of the neutron, its exact spin was ambiguous. Although it was assumed to be a spin 1/2 Dirac particle, the possibility that the neutron was a spin 3/2 particle lingered. The interactions of the neutron's magnetic moment with an external magnetic field were exploited to finally determine the spin of the neutron.[55] In 1949, Hughes and Burgy measured neutrons reflected from a ferromagnetic mirror and found that the angular distribution of the reflections was consistent with spin 1/2.[56] In 1954, Sherwood, Stephenson, and Bernstein employed neutrons in a Stern–Gerlach experiment that used a magnetic field to separate the neutron spin states. They recorded two such spin states, consistent with a spin 1/2 particle.[55][57]
As a fermion, the neutron is subject to the Pauli exclusion principle; two neutrons cannot have the same quantum numbers. This is the source of the degeneracy pressure which counteracts gravity in neutron stars and prevents them from forming black holes.[58]
Magnetic moment
Even though the neutron is a neutral particle, the magnetic moment of a neutron is not zero. The neutron is not affected by electric fields, but it is affected by magnetic fields. The value for the neutron's magnetic moment was first directly measured by Luis Alvarez and Felix Bloch at Berkeley, California, in 1940.[59] Alvarez and Bloch determined the magnetic moment of the neutron to be μn= −1.93(2) μN, where μN is the nuclear magneton. The neutron's magnetic moment has a negative value, because its orientation is opposite to the neutron's spin.[60]
The magnetic moment of the neutron is an indication of its quark substructure and internal charge distribution.[61] In the quark model for hadrons, the neutron is composed of one up quark (charge +2/3 e) and two down quarks (charge −1/3 e).[61] The magnetic moment of the neutron can be modeled as a sum of the magnetic moments of the constituent quarks.[62] The calculation assumes that the quarks behave like pointlike Dirac particles, each having their own magnetic moment. Simplistically, the magnetic moment of the neutron can be viewed as resulting from the vector sum of the three quark magnetic moments, plus the orbital magnetic moments caused by the movement of the three charged quarks within the neutron.
In one of the early successes of the Standard Model, in 1964 Mirza A.B. Beg, Benjamin W. Lee, and Abraham Pais calculated the ratio of proton to neutron magnetic moments to be −3/2 (or a ratio of −1.5), which agrees with the experimental value to within 3%.[63][64][65] The measured value for this ratio is −1.45989805(34).[4]
The above treatment compares neutrons with protons, allowing the complex behavior of quarks to be subtracted out between models, and merely exploring what the effects would be of differing quark charges (or quark type). Such calculations are enough to show that the interior of neutrons is very much like that of protons, save for the difference in quark composition with a down quark in the neutron replacing an up quark in the proton.
The neutron magnetic moment can be roughly computed by assuming a simple nonrelativistic, quantum mechanical wavefunction for baryons composed of three quarks. A straightforward calculation gives fairly accurate estimates for the magnetic moments of neutrons, protons, and other baryons.[62] For a neutron, the result of this calculation is that the magnetic moment of the neutron is given by μn= 4/3 μd − 1/3 μu, where μd and μu are the magnetic moments for the down and up quarks, respectively. This result combines the intrinsic magnetic moments of the quarks with their orbital magnetic moments, and assumes the three quarks are in a particular, dominant quantum state.
| Baryon | Magnetic moment of quark model |
Computed () |
Observed () |
|---|---|---|---|
| p | 4/3 μu − 1/3 μd | 2.79 | 2.793 |
| n | 4/3 μd − 1/3 μu | −1.86 | −1.913 |
The results of this calculation are encouraging, but the masses of the up or down quarks were assumed to be 1/3 the mass of a nucleon.[62] The masses of the quarks are actually only about 1% that of a nucleon.[66] The discrepancy stems from the complexity of the Standard Model for nucleons, where most of their mass originates in the gluon fields, virtual particles, and their associated energy that are essential aspects of the strong force.[66][67] Furthermore, the complex system of quarks and gluons that constitute a neutron requires a relativistic treatment.[68] But the nucleon magnetic moment has been successfully computed numerically from first principles, including all of the effects mentioned and using more realistic values for the quark masses. The calculation gave results that were in fair agreement with measurement, but it required significant computing resources.[69][70]
Electric charge
The total electric charge of the neutron is 0 e. This zero value has been tested experimentally, and the present experimental limit for the charge of the neutron is −2(8)×10−22 e,[6] or −3(13)×10−41 C. This value is consistent with zero, given the experimental uncertainties (indicated in parentheses). By comparison, the charge of the proton is +1 e.
Structure and geometry of charge distribution
An article published in 2007 featuring a model-independent analysis concluded that the neutron has a negatively charged exterior, a positively charged middle, and a negative core.[71] In a simplified classical view, the negative "skin" of the neutron assists it to be attracted to the protons with which it interacts in the nucleus; but the main attraction between neutrons and protons is via the nuclear force, which does not involve electric charge.
The simplified classical view of the neutron's charge distribution also "explains" the fact that the neutron magnetic dipole points in the opposite direction from its spin angular momentum vector (as compared to the proton). This gives the neutron, in effect, a magnetic moment which resembles a negatively charged particle. This can be reconciled classically with a neutral neutron composed of a charge distribution in which the negative sub-parts of the neutron have a larger average radius of distribution, and therefore contribute more to the particle's magnetic dipole moment, than do the positive parts that are, on average, nearer the core.
Electric dipole moment
The Standard Model of particle physics predicts a tiny separation of positive and negative charge within the neutron leading to a permanent electric dipole moment.[72] But the predicted value is well below the current sensitivity of experiments. From several unsolved puzzles in particle physics, it is clear that the Standard Model is not the final and full description of all particles and their interactions. New theories going beyond the Standard Model generally lead to much larger predictions for the electric dipole moment of the neutron. Currently, there are at least four experiments trying to measure for the first time a finite neutron electric dipole moment, including:
- Cryogenic neutron EDM experiment being set up at the Institut Laue–Langevin[73]
- nEDM experiment under construction at the new UCN source at the Paul Scherrer Institute[74]
- nEDM experiment being envisaged at the Spallation Neutron Source[75][76]
- nEDM experiment being built at the Institut Laue–Langevin[77]
Antineutron
The antineutron is the antiparticle of the neutron. It was discovered by Bruce Cork in 1956, a year after the antiproton was discovered. CPT-symmetry puts strong constraints on the relative properties of particles and antiparticles, so studying antineutrons provides stringent tests on CPT-symmetry. The fractional difference in the masses of the neutron and antineutron is (9±6)×10−5. Since the difference is only about two standard deviations away from zero, this does not give any convincing evidence of CPT-violation.[14]
Neutron compounds
Dineutrons and tetraneutrons
The dineutron is considered an unbound isotope with lifetimes around 10-22 seconds. The first evidence for this state was reported by Haddock et al. in 1965.[78]: 275 In 2012, Artemis Spyrou from Michigan State University and coworkers reported that they observed, for the first time, direct dineutron emission in the decay of 16Be. The dineutron character is evidenced by a small emission angle between the two neutrons. The authors measured the two-neutron separation energy to be 1.35(10) MeV, in good agreement with shell model calculations, using standard interactions for this mass region.[79]
Evidence for unbound clusters of 4 neutrons, or tetraneutron as resonances in the disintegration of beryllium-14 nuclei,[80] in 8He-8Be interactions,[81] and collisions of 4He nuclei give an estimated lifetime around 10-22 seconds.[82] These discoveries should deepen our understanding of the nuclear forces.[83][84]
Neuron stars and neutron matter
At extremely high pressures and temperatures, nucleons and electrons are believed to collapse into bulk neutronic matter, called neutron matter. This is presumed to happen in neutron stars.[85]
The extreme pressure inside a neutron star may deform the neutrons into a cubic symmetry, allowing tighter packing of neutrons.[86]
Detection
The common means of detecting a charged particle by looking for a track of ionization (such as in a cloud chamber) does not work for neutrons directly. Neutrons that elastically scatter off atoms can create an ionization track that is detectable, but the experiments are not as simple to carry out; other means for detecting neutrons, consisting of allowing them to interact with atomic nuclei, are more commonly used. The commonly used methods to detect neutrons can therefore be categorized according to the nuclear processes relied upon, mainly neutron capture or elastic scattering.[87]
Neutron detection by neutron capture
A common method for detecting neutrons involves converting the energy released from neutron capture reactions into electrical signals. Certain nuclides have a high neutron capture cross section, which is the probability of absorbing a neutron. Upon neutron capture, the compound nucleus emits more easily detectable radiation, for example an alpha particle, which is then detected. The nuclides 3
He
, 6
Li
, 10
B
, 233
U
, 235
U
, 237
Np
, and 239
Pu
are useful for this purpose.
Neutron detection by elastic scattering
Neutrons can elastically scatter off nuclei, causing the struck nucleus to recoil. Kinematically, a neutron can transfer more energy to a light nucleus such as hydrogen or helium than to a heavier nucleus. Detectors relying on elastic scattering are called fast neutron detectors. Recoiling nuclei can ionize and excite further atoms through collisions. Charge and/or scintillation light produced in this way can be collected to produce a detected signal. A major challenge in fast neutron detection is discerning such signals from erroneous signals produced by gamma radiation in the same detector. Methods such as pulse shape discrimination can be used in distinguishing neutron signals from gamma-ray signals, although certain inorganic scintillator-based detectors have been developed [88][89] to selectively detect neutrons in mixed radiation fields inherently without any additional techniques.
Fast neutron detectors have the advantage of not requiring a moderator, and are therefore capable of measuring the neutron's energy, time of arrival, and in certain cases direction of incidence.
Sources and production
Free neutrons are unstable, although they have the longest half-life of any unstable subatomic particle by several orders of magnitude. Their half-life is still only about 10 minutes, so they can be obtained only from sources that produce them continuously.
Natural neutron background. A small natural background flux of free neutrons exists everywhere on Earth.[90] In the atmosphere and deep into the ocean, the "neutron background" is caused by muons produced by cosmic ray interaction with the atmosphere. These high-energy muons are capable of penetration to considerable depths in water and soil. There, in striking atomic nuclei, among other reactions they induce spallation reactions in which a neutron is liberated from the nucleus. Within the Earth's crust a second source is neutrons produced primarily by spontaneous fission of uranium and thorium present in crustal minerals. The neutron background is not strong enough to be a biological hazard, but it is of importance to very high resolution particle detectors that are looking for very rare events, such as (hypothesized) interactions that might be caused by particles of dark matter.[90] Recent research has shown that even thunderstorms can produce neutrons with energies of up to several tens of MeV.[91] Recent research has shown that the fluence of these neutrons lies between 10−9 and 10−13 per ms and per m2 depending on the detection altitude. The energy of most of these neutrons, even with initial energies of 20 MeV, decreases down to the keV range within 1 ms.[92]
Even stronger neutron background radiation is produced at the surface of Mars, where the atmosphere is thick enough to generate neutrons from cosmic ray muon production and neutron-spallation, but not thick enough to provide significant protection from the neutrons produced. These neutrons not only produce a Martian surface neutron radiation hazard from direct downward-going neutron radiation but may also produce a significant hazard from reflection of neutrons from the Martian surface, which will produce reflected neutron radiation penetrating upward into a Martian craft or habitat from the floor.[93]
Sources of neutrons for research. These include certain types of radioactive decay (spontaneous fission and neutron emission), and from certain nuclear reactions. Convenient nuclear reactions include tabletop reactions such as natural alpha and gamma bombardment of certain nuclides, often beryllium or deuterium, and induced nuclear fission, such as occurs in nuclear reactors. In addition, high-energy nuclear reactions (such as occur in cosmic radiation showers or accelerator collisions) also produce neutrons from disintegration of target nuclei. Small (tabletop) particle accelerators optimized to produce free neutrons in this way, are called neutron generators.
In practice, the most commonly used small laboratory sources of neutrons use radioactive decay to power neutron production. One noted neutron-producing radioisotope, californium-252 decays (half-life 2.65 years) by spontaneous fission 3% of the time with production of 3.7 neutrons per fission, and is used alone as a neutron source from this process. Nuclear reaction sources (that involve two materials) powered by radioisotopes use an alpha decay source plus a beryllium target, or else a source of high-energy gamma radiation from a source that undergoes beta decay followed by gamma decay, which produces photoneutrons on interaction of the high-energy gamma ray with ordinary stable beryllium, or else with the deuterium in heavy water. A popular source of the latter type is radioactive antimony-124 plus beryllium, a system with a half-life of 60.9 days, which can be constructed from natural antimony (which is 42.8% stable antimony-123) by activating it with neutrons in a nuclear reactor, then transported to where the neutron source is needed.[94]
_in_Grenoble%252C_France.jpg.webp)
Nuclear fission reactors naturally produce free neutrons; their role is to sustain the energy-producing chain reaction. The intense neutron radiation can also be used to produce various radioisotopes through the process of neutron activation, which is a type of neutron capture.
Experimental nuclear fusion reactors produce free neutrons as a waste product. But it is these neutrons that possess most of the energy, and converting that energy to a useful form has proved a difficult engineering challenge. Fusion reactors that generate neutrons are likely to create radioactive waste, but the waste is composed of neutron-activated lighter isotopes, which have relatively short (50–100 years) decay periods as compared to typical half-lives of 10,000 years[95] for fission waste, which is long due primarily to the long half-life of alpha-emitting transuranic actinides.[96] Some nuclear fusion-fission hybrids are proposed to make use of those neutrons to either maintain a subcritical reactor or to aid in nuclear transmutation of harmful long lived nuclear waste to shorter lived or stable nuclides.
Neutron beams and modification of beams after production
Free neutron beams are obtained from neutron sources by neutron transport. For access to intense neutron sources, researchers must go to a specialized neutron facility that operates a research reactor or a spallation source.
The neutron's lack of total electric charge makes it difficult to steer or accelerate them. Charged particles can be accelerated, decelerated, or deflected by electric or magnetic fields. These methods have little effect on neutrons. But some effects may be attained by use of inhomogeneous magnetic fields because of the neutron's magnetic moment. Neutrons can be controlled by methods that include moderation, reflection, and velocity selection. Thermal neutrons can be polarized by transmission through magnetic materials in a method analogous to the Faraday effect for photons. Cold neutrons of wavelengths of 6–7 angstroms can be produced in beams of a high degree of polarization, by use of magnetic mirrors and magnetized interference filters.[97]
Applications
| Science with neutrons |
|---|
 |
| Foundations |
| Neutron scattering |
| Other applications |
|
| Infrastructure |
|
| Neutron facilities |
The neutron plays an important role in many nuclear reactions. For example, neutron capture often results in neutron activation, inducing radioactivity. In particular, knowledge of neutrons and their behavior has been important in the development of nuclear reactors and nuclear weapons. The fissioning of elements like uranium-235 and plutonium-239 is caused by their absorption of neutrons.
Cold, thermal, and hot neutron radiation is commonly employed in neutron scattering facilities for neutron diffraction, small-angle neutron scattering, and neutron reflectometry. Slow neutron matter waves exhibit properties similar to geometrical and wave optics of light, including reflection, refraction, diffraction, and interference.[98] Neutrons are complementary to X-rays in terms of atomic contrasts by different scattering cross sections; sensitivity to magnetism; energy range for inelastic neutron spectroscopy; and deep penetration into matter.
The development of "neutron lenses" based on total internal reflection within hollow glass capillary tubes or by reflection from dimpled aluminum plates has driven ongoing research into neutron microscopy and neutron/gamma ray tomography.[99][100][101][102]
A major use of neutrons is to excite delayed and prompt gamma rays from elements in materials. This forms the basis of neutron activation analysis (NAA) and prompt gamma neutron activation analysis (PGNAA). NAA is most often used to analyze small samples of materials in a nuclear reactor whilst PGNAA is most often used to analyze subterranean rocks around bore holes and industrial bulk materials on conveyor belts.
Another use of neutron emitters is the detection of light nuclei, in particular the hydrogen found in water molecules. When a fast neutron collides with a light nucleus, it loses a large fraction of its energy. By measuring the rate at which slow neutrons return to the probe after reflecting off of hydrogen nuclei, a neutron probe may determine the water content in soil.
Medical therapies
Because neutron radiation is both penetrating and ionizing, it can be exploited for medical treatments. However, neutron radiation can have the unfortunate side-effect of leaving the affected area radioactive. Neutron tomography is therefore not a viable medical application.
Fast neutron therapy uses high-energy neutrons typically greater than 20 MeV to treat cancer. Radiation therapy of cancers is based upon the biological response of cells to ionizing radiation. If radiation is delivered in small sessions to damage cancerous areas, normal tissue will have time to repair itself, while tumor cells often cannot.[103] Neutron radiation can deliver energy to a cancerous region at a rate an order of magnitude larger than gamma radiation.[104]
Beams of low-energy neutrons are used in boron neutron capture therapy to treat cancer. In boron neutron capture therapy, the patient is given a drug that contains boron and that preferentially accumulates in the tumor to be targeted. The tumor is then bombarded with very low-energy neutrons (although often higher than thermal energy) which are captured by the boron-10 isotope in the boron, which produces an excited state of boron-11 that then decays to produce lithium-7 and an alpha particle that have sufficient energy to kill the malignant cell, but insufficient range to damage nearby cells. For such a therapy to be applied to the treatment of cancer, a neutron source having an intensity of the order of a thousand million (109) neutrons per second per cm2 is preferred. Such fluxes require a research nuclear reactor.
Protection
Exposure to free neutrons can be hazardous, since the interaction of neutrons with molecules in the body can cause disruption to molecules and atoms, and can also cause reactions that give rise to other forms of radiation (such as protons).[7] The normal precautions of radiation protection apply: Avoid exposure, stay as far from the source as possible, and keep exposure time to a minimum. But particular thought must be given to how to protect from neutron exposure. For other types of radiation, e.g., alpha particles, beta particles, or gamma rays, material of a high atomic number and with high density makes for good shielding; frequently, lead is used. However, this approach will not work with neutrons, since the absorption of neutrons does not increase straightforwardly with atomic number, as it does with alpha, beta, and gamma radiation. Instead one needs to look at the particular interactions neutrons have with matter (see the section on detection above). For example, hydrogen-rich materials are often used to shield against neutrons, since ordinary hydrogen both scatters and slows neutrons. This often means that simple concrete blocks or even paraffin-loaded plastic blocks afford better protection from neutrons than do far more dense materials. After slowing, neutrons may then be absorbed with an isotope that has high affinity for slow neutrons without causing secondary capture radiation, such as lithium-6.
Hydrogen-rich ordinary water effects neutron absorption in nuclear fission reactors: Usually, neutrons are so strongly absorbed by normal water that fuel enrichment with a fissionable isotope is required. (The number of neutrons produced per fission depends primarily on the fission products. The average is roughly 2.5 to 3.0 and at least one, on average, must evade capture in order to sustain the nuclear chain reaction.) The deuterium in heavy water has a very much lower absorption affinity for neutrons than does protium (normal light hydrogen). Deuterium is, therefore, used in CANDU-type reactors, in order to slow (moderate) neutron velocity, to increase the probability of nuclear fission compared to neutron capture.
Neutron temperature
Thermal neutrons
Thermal neutrons are free neutrons whose energies have a Maxwell–Boltzmann distribution with kT = 0.0253 eV (4.0×10−21 J) at room temperature. This gives characteristic (not average, or median) speed of 2.2 km/s. The name 'thermal' comes from their energy being that of the room temperature gas or material they are permeating. (see kinetic theory for energies and speeds of molecules). After a number of collisions (often in the range of 10–20) with nuclei, neutrons arrive at this energy level, provided that they are not absorbed.
In many substances, thermal neutron reactions show a much larger effective cross-section than reactions involving faster neutrons, and thermal neutrons can therefore be absorbed more readily (i.e., with higher probability) by any atomic nuclei that they collide with, creating a heavier – and often unstable – isotope of the chemical element as a result.
Most fission reactors use a neutron moderator to slow down, or thermalize the neutrons that are emitted by nuclear fission so that they are more easily captured, causing further fission. Others, called fast breeder reactors, use fission energy neutrons directly.
Cold neutrons
Cold neutrons are thermal neutrons that have been equilibrated in a very cold substance such as liquid deuterium. Such a cold source is placed in the moderator of a research reactor or spallation source. Cold neutrons are particularly valuable for neutron scattering experiments.[105]
The use of cold and very cold neutrons (VCN) have been a bit limited compared to the use of thermal neutrons due to the relatively lower flux and lack in optical components. However, Innovative solutions have been proposed to offer more options to the scientific community to promote the use of VCN.[106][107]
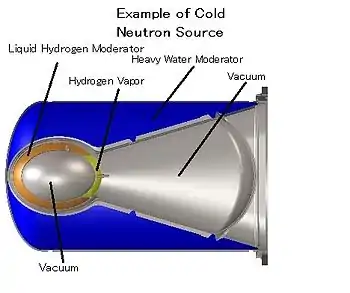
Ultracold neutrons
Ultracold neutrons are produced by inelastic scattering of cold neutrons in substances with a low neutron absorption cross section at a temperature of a few kelvins, such as solid deuterium[108] or superfluid helium.[109] An alternative production method is the mechanical deceleration of cold neutrons exploiting the Doppler shift.[110][111]
Fission energy neutrons
A fast neutron is a free neutron with a kinetic energy level close to 1 MeV (1.6×10−13 J), hence a speed of ~14000 km/s (~ 5% of the speed of light). They are named fission energy or fast neutrons to distinguish them from lower-energy thermal neutrons, and high-energy neutrons produced in cosmic showers or accelerators. Fast neutrons are produced by nuclear processes such as nuclear fission. Neutrons produced in fission, as noted above, have a Maxwell–Boltzmann distribution of kinetic energies from 0 to ~14 MeV, a mean energy of 2 MeV (for 235U fission neutrons), and a mode of only 0.75 MeV, which means that more than half of them do not qualify as fast (and thus have almost no chance of initiating fission in fertile materials, such as 238U and 232Th).
Fast neutrons can be made into thermal neutrons via a process called moderation. This is done with a neutron moderator. In reactors, typically heavy water, light water, or graphite are used to moderate neutrons.
Fusion neutrons
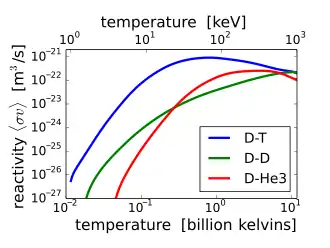
D–T (deuterium–tritium) fusion is the fusion reaction that produces the most energetic neutrons, with 14.1 MeV of kinetic energy and traveling at 17% of the speed of light. D–T fusion is also the easiest fusion reaction to ignite, reaching near-peak rates even when the deuterium and tritium nuclei have only a thousandth as much kinetic energy as the 14.1 MeV that will be produced.
14.1 MeV neutrons have about 10 times as much energy as fission neutrons, and are very effective at fissioning even non-fissile heavy nuclei, and these high-energy fissions produce more neutrons on average than fissions by lower-energy neutrons. This makes D–T fusion neutron sources such as proposed tokamak power reactors useful for transmutation of transuranic waste. 14.1 MeV neutrons can also produce neutrons by knocking them loose from nuclei.
On the other hand, these very high-energy neutrons are less likely to simply be captured without causing fission or spallation. For these reasons, nuclear weapon design extensively uses D–T fusion 14.1 MeV neutrons to cause more fission. Fusion neutrons are able to cause fission in ordinarily non-fissile materials, such as depleted uranium (uranium-238), and these materials have been used in the jackets of thermonuclear weapons. Fusion neutrons also can cause fission in substances that are unsuitable or difficult to make into primary fission bombs, such as reactor grade plutonium. This physical fact thus causes ordinary non-weapons grade materials to become of concern in certain nuclear proliferation discussions and treaties.
Other fusion reactions produce much less energetic neutrons. D–D fusion produces a 2.45 MeV neutron and helium-3 half of the time, and produces tritium and a proton but no neutron the rest of the time. D–3He fusion produces no neutron.
Intermediate-energy neutrons
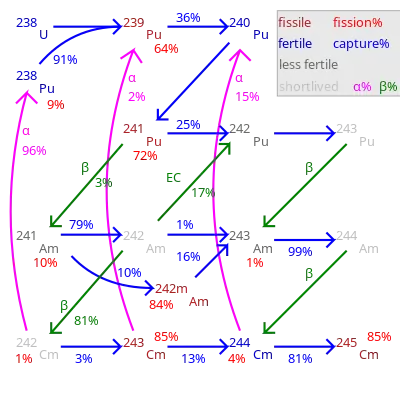
A fission energy neutron that has slowed down but not yet reached thermal energies is called an epithermal neutron.
Cross sections for both capture and fission reactions often have multiple resonance peaks at specific energies in the epithermal energy range. These are of less significance in a fast-neutron reactor, where most neutrons are absorbed before slowing down to this range, or in a well-moderated thermal reactor, where epithermal neutrons interact mostly with moderator nuclei, not with either fissile or fertile actinide nuclides. But in a partially moderated reactor with more interactions of epithermal neutrons with heavy metal nuclei, there are greater possibilities for transient changes in reactivity that might make reactor control more difficult.
Ratios of capture reactions to fission reactions are also worse (more captures without fission) in most nuclear fuels such as plutonium-239, making epithermal-spectrum reactors using these fuels less desirable, as captures not only waste the one neutron captured but also usually result in a nuclide that is not fissile with thermal or epithermal neutrons, though still fissionable with fast neutrons. The exception is uranium-233 of the thorium cycle, which has good capture-fission ratios at all neutron energies.
High-energy neutrons
High-energy neutrons have much more energy than fission energy neutrons and are generated as secondary particles by particle accelerators or in the atmosphere from cosmic rays. These high-energy neutrons are extremely efficient at ionization and far more likely to cause cell death than X-rays or protons.[112][113]
See also
- Ionizing radiation
- Isotope
- List of particles
- Neutron radiation and the Sievert radiation scale
- Neutronium
- Nuclear reaction
- Nucleosynthesis
- Thermal-neutron reactor
Neutron sources
Processes involving neutrons
References
- ↑ Ernest Rutherford Archived 2011-08-03 at the Wayback Machine. Chemed.chem.purdue.edu. Retrieved on 2012-08-16.
- 1 2 1935 Nobel Prize in Physics Archived 2017-10-03 at the Wayback Machine. Nobelprize.org. Retrieved on 2012-08-16.
- 1 2 "2018 CODATA recommended values" https://physics.nist.gov/cuu/Constants/index.html Archived 2018-01-22 at the Wayback Machine
- 1 2 3 4 5 6 Mohr, P.J.; Taylor, B.N. and Newell, D.B. (2014), "The 2014 CODATA Recommended Values of the Fundamental Physical Constants" Archived 2013-10-09 at the Wayback Machine (Web Version 7.0). The database was developed by J. Baker, M. Douma, and S. Kotochigova. (2014). National Institute of Standards and Technology, Gaithersburg, Maryland 20899.
- ↑ Zyla, P. A. (2020). "n MEAN LIFE". PDG Live: 2020 Review of Particle Physics. Particle Data Group. Archived from the original on 17 January 2021. Retrieved 25 February 2021.
- 1 2 Olive, K.A.; (Particle Data Group); et al. (2014). "Review of Particle Physics" (PDF). Chinese Physics C. 38 (9): 1–708. arXiv:1412.1408. Bibcode:2014ChPhC..38i0001O. doi:10.1088/1674-1137/38/9/090001. PMID 10020536. S2CID 118395784. Archived (PDF) from the original on 2020-06-01. Retrieved 2017-10-26.
- 1 2 3 Glasstone, Samuel; Dolan, Philip J., eds. (1977), The Effects of Nuclear Weapons (3rd ed.), U.S. Dept. of Defense and Energy Research and Development Administration, U.S. Government Printing Office, ISBN 978-1-60322-016-3
- ↑ Giancoli, Douglas C. (1984). General physics. Englewood Cliffs, N.J: Prentice-Hall. ISBN 978-0-13-350884-0. OCLC 1033640549.
- ↑ Nudat 2 Archived 2009-08-17 at the Wayback Machine. Nndc.bnl.gov. Retrieved on 2010-12-04.
- ↑ Thomas, A.W.; Weise, W. (2001), The Structure of the Nucleon, Wiley-WCH, Berlin, ISBN 978-3-527-40297-7
- ↑ Particle Data Group Summary Data Table on Baryons Archived 2011-09-10 at the Wayback Machine. lbl.gov (2007). Retrieved on 2012-08-16.
- ↑ Povh, B.; Rith, K.; Scholz, C.; Zetsche, F. (2002). Particles and Nuclei: An Introduction to the Physical Concepts. Berlin: Springer-Verlag. p. 73. ISBN 978-3-540-43823-6.
- ↑ Basdevant, J.-L.; Rich, J.; Spiro, M. (2005). Fundamentals in Nuclear Physics. Springer. p. 155. ISBN 978-0-387-01672-6.
- 1 2 Nakamura, K (2010). "Review of Particle Physics". Journal of Physics G. 37 (7A): 1–708. Bibcode:2010JPhG...37g5021N. doi:10.1088/0954-3899/37/7A/075021. hdl:10481/34593. PMID 10020536. PDF with 2011 partial update for the 2012 edition Archived 2012-09-20 at the Wayback Machine. The exact value of the mean lifetime is still uncertain, due to conflicting results from experiments. The Particle Data Group reports values up to six seconds apart (more than four standard deviations), commenting that "our 2006, 2008, and 2010 Reviews stayed with 885.7±0.8 s; but we noted that in light of SEREBROV 05 our value should be regarded as suspect until further experiments clarified matters. Since our 2010 Review, PICHLMAIER 10 has obtained a mean life of 880.7±1.8 s, closer to the value of SEREBROV 05 than to our average. And SEREBROV 10B[...] claims their values should be lowered by about 6 s, which would bring them into line with the two lower values. But those re-evaluations have not received an enthusiastic response from the experimenters in question; and in any case the Particle Data Group would have to await published changes (by those experimenters) of published values. At this point, we can think of nothing better to do than to average the seven best but discordant measurements, getting 881.5±1.5 s. Note that the error includes a scale factor of 2.7. This is a jump of 4.2 old (and 2.8 new) standard deviations. This state of affairs is a particularly unhappy one, because the value is so important. We again call upon the experimenters to clear this up."
- ↑ Tanabashi, M. (2018). "The Review of Particle Physics". Physical Review D. 54 (1): 1653. doi:10.1103/physrevd.54.1. PMID 10020536. Archived from the original on 2020-10-19. Retrieved 2020-10-14.
- ↑ Basic Ideas and Concepts in Nuclear Physics: An Introductory Approach, Third Edition; K. Heyde Taylor & Francis 2004. Print ISBN 978-0-7503-0980-6, 978-1-4200-5494-1. doi:10.1201/9781420054941. full text
- ↑ Sir James Chadwick's Discovery of Neutrons Archived 2011-10-26 at the Wayback Machine. ANS Nuclear Cafe. Retrieved on 2012-08-16.
- ↑ Adair, R.K. (1989). The Great Design: Particles, Fields, and Creation. Oxford University Press. p. 214. Bibcode:1988gdpf.book.....A.
- ↑ Cottingham, W.N.; Greenwood, D.A. (1986). An Introduction to Nuclear Physics. Cambridge University Press. ISBN 9780521657334.
- 1 2 Rutherford, E. (1920). "Nuclear Constitution of Atoms". Proceedings of the Royal Society A. 97 (686): 374–400. Bibcode:1920RSPSA..97..374R. doi:10.1098/rspa.1920.0040.
- ↑ Harkins, William (1921). "The constitution and stability of atomic nuclei. (A contribution to the subject of inorganic evolution.)". Philos. Mag. 42 (249): 305. doi:10.1080/14786442108633770.
- 1 2 Feather, N. (1960). "A history of neutrons and nuclei. Part 1". Contemporary Physics. 1 (3): 191–203. Bibcode:1960ConPh...1..191F. doi:10.1080/00107516008202611.
- ↑ Pauli, Wolfgang; Hermann, A.; Meyenn, K.v; Weisskopff, V.F (1985). "Das Jahr 1932 die Entdeckung des Neutrons". Wolfgang Pauli. Sources in the History of Mathematics and Physical Sciences. Vol. 6. pp. 105–144. doi:10.1007/978-3-540-78801-0_3. ISBN 978-3-540-13609-5.
- ↑ Hendry, John, ed. (1984). Cambridge Physics in the Thirties. Bristol: Adam Hilger. ISBN 978-0852747612.
- ↑ Brown, Laurie M. (1978). "The idea of the neutrino". Physics Today. 31 (9): 23–28. Bibcode:1978PhT....31i..23B. doi:10.1063/1.2995181.
- ↑ Friedlander G., Kennedy J.W. and Miller J.M. (1964) Nuclear and Radiochemistry (2nd edition), Wiley, pp. 22–23 and 38–39
- 1 2 Stuewer, Roger H. (1985). "Niels Bohr and Nuclear Physics". In French, A.P.; Kennedy, P.J. (eds.). Niels Bohr: A Centenary Volume. Harvard University Press. pp. 197–220. ISBN 978-0674624160.
- ↑ Pais, Abraham (1986). Inward Bound. Oxford: Oxford University Press. p. 299. ISBN 978-0198519973.
- ↑ Klein, O. (1929). "Die Reflexion von Elektronen an einem Potentialsprung nach der relativistischen Dynamik von Dirac". Zeitschrift für Physik. 53 (3–4): 157–165. Bibcode:1929ZPhy...53..157K. doi:10.1007/BF01339716. S2CID 121771000.
- ↑ Bothe, W.; Becker, H. (1930). "Künstliche Erregung von Kern-γ-Strahlen" [Artificial excitation of nuclear γ-radiation]. Zeitschrift für Physik. 66 (5–6): 289–306. Bibcode:1930ZPhy...66..289B. doi:10.1007/BF01390908. S2CID 122888356.
- ↑ Becker, H.; Bothe, W. (1932). "Die in Bor und Beryllium erregten γ-Strahlen" [Γ-rays excited in boron and beryllium]. Zeitschrift für Physik. 76 (7–8): 421–438. Bibcode:1932ZPhy...76..421B. doi:10.1007/BF01336726. S2CID 121188471.
- ↑ Joliot-Curie, Irène & Joliot, Frédéric (1932). "Émission de protons de grande vitesse par les substances hydrogénées sous l'influence des rayons γ très pénétrants" [Emission of high-speed protons by hydrogenated substances under the influence of very penetrating γ-rays]. Comptes Rendus. 194: 273. Archived from the original on 2022-03-04. Retrieved 2012-06-16.
- ↑ Brown, Andrew (1997). The Neutron and the Bomb: A Biography of Sir James Chadwick. Oxford University Press. ISBN 978-0-19-853992-6.
- ↑ Chadwick, James (1932). "Possible Existence of a Neutron" (PDF). Nature. 129 (3252): 312. Bibcode:1932Natur.129Q.312C. doi:10.1038/129312a0. S2CID 4076465.
- ↑ "Atop the Physics Wave: Rutherford Back in Cambridge, 1919–1937". Rutherford's Nuclear World. American Institute of Physics. 2011–2014. Archived from the original on 21 October 2014. Retrieved 19 August 2014.
- ↑ Chadwick, J. (1933). "Bakerian Lecture. The Neutron". Proceedings of the Royal Society A. 142 (846): 1–25. Bibcode:1933RSPSA.142....1C. doi:10.1098/rspa.1933.0152.
- ↑ Heisenberg, W. (1932). "Über den Bau der Atomkerne. I". Zeitschrift für Physik. 77 (1–2): 1–11. Bibcode:1932ZPhy...77....1H. doi:10.1007/BF01342433. S2CID 186218053.
- ↑ Heisenberg, W. (1932). "Über den Bau der Atomkerne. II". Zeitschrift für Physik. 78 (3–4): 156–164. Bibcode:1932ZPhy...78..156H. doi:10.1007/BF01337585. S2CID 186221789.
- ↑ Heisenberg, W. (1933). "Über den Bau der Atomkerne. III". Zeitschrift für Physik. 80 (9–10): 587–596. Bibcode:1933ZPhy...80..587H. doi:10.1007/BF01335696. S2CID 126422047.
- ↑ Iwanenko, D. (1932). "The Neutron Hypothesis". Nature. 129 (3265): 798. Bibcode:1932Natur.129..798I. doi:10.1038/129798d0. S2CID 4096734.
- ↑ Miller A.I. (1995) Early Quantum Electrodynamics: A Sourcebook, Cambridge University Press, Cambridge, ISBN 0521568919, pp. 84–88.
- ↑ Wilson, Fred L. (1968). "Fermi's Theory of Beta Decay". American Journal of Physics. 36 (12): 1150–1160. Bibcode:1968AmJPh..36.1150W. doi:10.1119/1.1974382.
- ↑ Chadwick, J.; Goldhaber, M. (1934). "A nuclear photo-effect: disintegration of the diplon by gamma rays". Nature. 134 (3381): 237–238. Bibcode:1934Natur.134..237C. doi:10.1038/134237a0. S2CID 4137231.
- ↑ Chadwick, J.; Goldhaber, M. (1935). "A nuclear photoelectric effect". Proceedings of the Royal Society of London A. 151 (873): 479–493. Bibcode:1935RSPSA.151..479C. doi:10.1098/rspa.1935.0162.
- ↑ Cooper, Dan (1999). Enrico Fermi: And the Revolutions in Modern physics. New York: Oxford University Press. ISBN 978-0-19-511762-2. OCLC 39508200.
- ↑ Hahn, O. & Strassmann, F. (1939). "Über den Nachweis und das Verhalten der bei der Bestrahlung des Urans mittels Neutronen entstehenden Erdalkalimetalle" [On the detection and characteristics of the alkaline earth metals formed by irradiation of uranium with neutrons]. Die Naturwissenschaften. 27 (1): 11–15. Bibcode:1939NW.....27...11H. doi:10.1007/BF01488241. S2CID 5920336.
- ↑ Hahn, O. (1958). "The Discovery of Fission". Scientific American. 198 (2): 76–84. Bibcode:1958SciAm.198b..76H. doi:10.1038/scientificamerican0258-76.
- ↑ Rife, Patricia (1999). Lise Meitner and the dawn of the nuclear age. Basel, Switzerland: Birkhäuser. ISBN 978-0-8176-3732-3.
- ↑ Hahn, O.; Strassmann, F. (10 February 1939). "Proof of the Formation of Active Isotopes of Barium from Uranium and Thorium Irradiated with Neutrons; Proof of the Existence of More Active Fragments Produced by Uranium Fission". Die Naturwissenschaften. 27 (6): 89–95. Bibcode:1939NW.....27...89H. doi:10.1007/BF01488988. S2CID 33512939.
- ↑ "The Nobel Prize in Chemistry 1944". Nobel Foundation. Archived from the original on 2018-12-26. Retrieved 2007-12-17.
- ↑ Bernstein, Jeremy (2001). Hitler's uranium club: the secret recordings at Farm Hall. New York: Copernicus. p. 281. ISBN 978-0-387-95089-1.
- ↑ "The Nobel Prize in Chemistry 1944: Presentation Speech". Nobel Foundation. Archived from the original on 2007-10-25. Retrieved 2008-01-03.
- ↑ Greene, GL; et al. (1986). "New determination of the deuteron binding energy and the neutron mass". Physical Review Letters. 56 (8): 819–822. Bibcode:1986PhRvL..56..819G. doi:10.1103/PhysRevLett.56.819. PMID 10033294.
- ↑ Byrne, J. Neutrons, Nuclei, and Matter, Dover Publications, Mineola, New York, 2011, ISBN 0486482383, pp. 18–19
- 1 2 J. Byrne (2011). Neutrons, Nuclei and Matter: An exploration of the physics of slow neutrons. Mineola, NY: Dover Publications. pp. 28–31. ISBN 978-0486482385.
- ↑ Hughes, D.J.; Burgy, M.T. (1949). "Reflection and polarization of neutrons by magnetized mirrors" (PDF). Physical Review. 76 (9): 1413–1414. Bibcode:1949PhRv...76.1413H. doi:10.1103/PhysRev.76.1413. Archived from the original (PDF) on 2016-08-13. Retrieved 2016-06-26.
- ↑ Sherwood, J.E.; Stephenson, T.E.; Bernstein, S. (1954). "Stern-Gerlach experiment on polarized neutrons". Physical Review. 96 (6): 1546–1548. Bibcode:1954PhRv...96.1546S. doi:10.1103/PhysRev.96.1546.
- ↑ Bombaci, I. (1996). "The Maximum Mass of a Neutron Star". Astronomy and Astrophysics. 305: 871–877. Bibcode:1996A&A...305..871B.
- ↑ Alvarez, L.W; Bloch, F. (1940). "A quantitative determination of the neutron magnetic moment in absolute nuclear magnetons". Physical Review. 57 (2): 111–122. Bibcode:1940PhRv...57..111A. doi:10.1103/physrev.57.111.
- ↑ Tipler, Paul Allen; Llewellyn, Ralph A. (2002). Modern Physics (4 ed.). Macmillan. p. 310. ISBN 978-0-7167-4345-3. Archived from the original on 2022-04-07. Retrieved 2020-08-27.
- 1 2 Gell, Y.; Lichtenberg, D.B. (1969). "Quark model and the magnetic moments of proton and neutron". Il Nuovo Cimento A. Series 10. 61 (1): 27–40. Bibcode:1969NCimA..61...27G. doi:10.1007/BF02760010. S2CID 123822660.
- 1 2 3 Perkins, Donald H. (1982). Introduction to High Energy Physics. Addison Wesley, Reading, Massachusetts. pp. 201–202. ISBN 978-0-201-05757-7.
- ↑ Greenberg, O.W. (2009), "Color Charge Degree of Freedom in Particle Physics", Compendium of Quantum Physics, Springer Berlin Heidelberg, pp. 109–111, arXiv:0805.0289, doi:10.1007/978-3-540-70626-7_32, ISBN 978-3-540-70622-9, S2CID 17512393
- ↑ Beg, M.A.B.; Lee, B.W.; Pais, A. (1964). "SU(6) and electromagnetic interactions". Physical Review Letters. 13 (16): 514–517, erratum 650. Bibcode:1964PhRvL..13..514B. doi:10.1103/physrevlett.13.514.
- ↑ Sakita, B. (1964). "Electromagnetic properties of baryons in the supermultiplet scheme of elementary particles". Physical Review Letters. 13 (21): 643–646. Bibcode:1964PhRvL..13..643S. doi:10.1103/physrevlett.13.643.
- 1 2 Cho, Adrian (2 April 2010). "Mass of the Common Quark Finally Nailed Down". Science. American Association for the Advancement of Science. Archived from the original on 27 August 2015. Retrieved 27 September 2014.
- ↑ Wilczek, F. (2003). "The Origin of Mass" (PDF). MIT Physics Annual: 24–35. Archived (PDF) from the original on June 20, 2015.
- ↑ Ji, Xiangdong (1995). "A QCD Analysis of the Mass Structure of the Nucleon". Physical Review Letters. 74 (7): 1071–1074. arXiv:hep-ph/9410274. Bibcode:1995PhRvL..74.1071J. doi:10.1103/PhysRevLett.74.1071. PMID 10058927. S2CID 15148740.
- ↑ Martinelli, G.; Parisi, G.; Petronzio, R.; Rapuano, F. (1982). "The proton and neutron magnetic moments in lattice QCD" (PDF). Physics Letters B. 116 (6): 434–436. Bibcode:1982PhLB..116..434M. doi:10.1016/0370-2693(82)90162-9. Archived (PDF) from the original on 2020-04-20. Retrieved 2019-08-25.
- ↑ Kincade, Kathy (2 February 2015). "Pinpointing the magnetic moments of nuclear matter". Phys.org. Archived from the original on 2 May 2015. Retrieved May 8, 2015.
- ↑ Miller, G.A. (2007). "Charge Densities of the Neutron and Proton". Physical Review Letters. 99 (11): 112001. arXiv:0705.2409. Bibcode:2007PhRvL..99k2001M. doi:10.1103/PhysRevLett.99.112001. PMID 17930428. S2CID 119120565.
- ↑ "Pear-shaped particles probe big-bang mystery" (Press release). University of Sussex. 20 February 2006. Archived from the original on 2011-06-07. Retrieved 2009-12-14.
- ↑ A cryogenic experiment to search for the EDM of the neutron Archived 2012-02-16 at the Wayback Machine. Hepwww.rl.ac.uk. Retrieved on 2012-08-16.
- ↑ Search for the neutron electric dipole moment: nEDM Archived 2015-09-25 at the Wayback Machine. Nedm.web.psi.ch (2001-09-12). Retrieved on 2012-08-16.
- ↑ US nEDM ORNL experiment public page Archived 2017-04-30 at the Wayback Machine. Retrieved on 2017-02-08.
- ↑ SNS Neutron EDM Experiment Archived 2011-02-10 at the Wayback Machine. P25ext.lanl.gov. Retrieved on 2012-08-16.
- ↑ Measurement of the Neutron Electric Dipole Moment Archived 2011-08-23 at the Wayback Machine. Nrd.pnpi.spb.ru. Retrieved on 2012-08-16.
- ↑ Thoennessen, Michael (2016). Unbound Isotopes. Cham: Springer International Publishing. pp. 275–291. doi:10.1007/978-3-319-31763-2_16. ISBN 978-3-319-31761-8.
- ↑ Spyrou, A.; et al. (2012). "First Observation of Ground State Dineutron Decay: 16Be". Physical Review Letters. 108 (10): 102501. Bibcode:2012PhRvL.108j2501S. doi:10.1103/PhysRevLett.108.102501. PMID 22463404.
- ↑ Marqués, F. M.; Labiche, M.; Orr, N. A.; Angélique, J. C.; Axelsson, L.; Benoit, B.; Bergmann, U. C.; Borge, M. J. G.; Catford, W. N.; Chappell, S. P. G.; Clarke, N. M.; Costa, G.; Curtis, N.; D’Arrigo, A.; de Góes Brennand, E. (2002-04-01). "Detection of neutron clusters". Physical Review C. 65 (4). arXiv:nucl-ex/0111001. doi:10.1103/PhysRevC.65.044006. ISSN 0556-2813.
- ↑ Kisamori, K.; et al. (2016). "Candidate Resonant Tetraneutron State Populated by the He4(He8,Be8) Reaction". Physical Review Letters. 116 (5): 052501. Bibcode:2016PhRvL.116e2501K. doi:10.1103/PhysRevLett.116.052501. PMID 26894705.
- ↑ Duer, M.; Aumann, T.; Gernhäuser, R.; Panin, V.; Paschalis, S.; Rossi, D. M.; Achouri, N. L.; Ahn, D.; Baba, H.; Bertulani, C. A.; Böhmer, M.; Boretzky, K.; Caesar, C.; Chiga, N.; Corsi, A. (2022-06-23). "Observation of a correlated free four-neutron system". Nature. 606 (7915): 678–682. doi:10.1038/s41586-022-04827-6. ISSN 0028-0836. PMC 9217746. PMID 35732764.
- ↑ "Physicists find signs of four-neutron nucleus". 2016-02-24. Archived from the original on 2017-07-29. Retrieved 2017-06-27.
- ↑ Orr, Nigel (2016-02-03). "Can Four Neutrons Tango?". Physics. 9: 14. Bibcode:2016PhyOJ...9...14O. doi:10.1103/Physics.9.14.
- ↑ Gandolfi, Stefano; Gezerlis, Alexandros; Carlson, J. (2015-10-19). "Neutron Matter from Low to High Density". Annual Review of Nuclear and Particle Science. 65 (1): 303–328. arXiv:1501.05675. doi:10.1146/annurev-nucl-102014-021957. ISSN 0163-8998.
- ↑ Llanes-Estrada, Felipe J.; Moreno Navarro, Gaspar (2012). "Cubic neutrons". Modern Physics Letters A. 27 (6): 1250033–1–1250033–7. arXiv:1108.1859. Bibcode:2012MPLA...2750033L. doi:10.1142/S0217732312500332. S2CID 118407306.
- ↑ Knoll, Glenn F. (1979). "Ch. 14". Radiation Detection and Measurement. John Wiley & Sons. ISBN 978-0471495451.
- ↑ Ghosh, P.; W. Fu; M. J. Harrison; P. K. Doyle; N. S. Edwards; J. A. Roberts; D. S. McGregor (2018). "A high-efficiency, low-Ĉerenkov Micro-Layered Fast-Neutron Detector for the TREAT hodoscope". Nuclear Instruments and Methods in Physics Research Section A. 904: 100–106. Bibcode:2018NIMPA.904..100G. doi:10.1016/j.nima.2018.07.035. S2CID 126130994. Archived from the original on 2022-04-12. Retrieved 2020-04-14.
- ↑ Ghosh, P.; D. M. Nichols; W. Fu; J. A. Roberts; D. S. McGregor (2019). "Gamma-Ray Rejection of the SiPM-coupled Micro-Layered Fast-Neutron Detector". 2019 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC). pp. 1–3. doi:10.1109/NSS/MIC42101.2019.9059869. ISBN 978-1-7281-4164-0. S2CID 204877955.
- 1 2 Carson, M.J.; et al. (2004). "Neutron background in large-scale xenon detectors for dark matter searches". Astroparticle Physics. 21 (6): 667–687. arXiv:hep-ex/0404042. Bibcode:2004APh....21..667C. doi:10.1016/j.astropartphys.2004.05.001. S2CID 17887096.
- ↑ Köhn, C.; Ebert, U. (2015). "Calculation of beams of positrons, neutrons and protons associated with terrestrial gamma-ray flashes" (PDF). Journal of Geophysical Research: Atmospheres. 23 (4): 1620–1635. Bibcode:2015JGRD..120.1620K. doi:10.1002/2014JD022229. Archived (PDF) from the original on 2019-12-23. Retrieved 2019-08-25.
- ↑ Köhn, C.; Diniz, G.; Harakeh, Muhsin (2017). "Production mechanisms of leptons, photons, and hadrons and their possible feedback close to lightning leaders". Journal of Geophysical Research: Atmospheres. 122 (2): 1365–1383. Bibcode:2017JGRD..122.1365K. doi:10.1002/2016JD025445. PMC 5349290. PMID 28357174.
- ↑ Clowdsley, MS; Wilson, JW; Kim, MH; Singleterry, RC; Tripathi, RK; Heinbockel, JH; Badavi, FF; Shinn, JL (2001). "Neutron Environments on the Martian Surface" (PDF). Physica Medica. 17 (Suppl 1): 94–96. PMID 11770546. Archived from the original (PDF) on 2005-02-25.
- ↑ Byrne, J. Neutrons, Nuclei, and Matter, Dover Publications, Mineola, New York, 2011, ISBN 0486482383, pp. 32–33.
- ↑ "Isotopes and Radioactivity Tutorial". Archived from the original on 2020-02-14. Retrieved 2020-04-16.
- ↑ Science/Nature |Q&A: Nuclear fusion reactor Archived 2022-02-25 at the Wayback Machine. BBC News (2006-02-06). Retrieved on 2010-12-04.
- ↑ Byrne, J. Neutrons, Nuclei, and Matter, Dover Publications, Mineola, New York, 2011, ISBN 0486482383, p. 453.
- ↑ Klein, A G; Werner, S A (1983-03-01). "Neutron optics". Reports on Progress in Physics. IOP Publishing. 46 (3): 259–335. doi:10.1088/0034-4885/46/3/001. ISSN 0034-4885. S2CID 250903152.
- ↑ Kumakhov, M.A.; Sharov, V.A. (1992). "A neutron lens". Nature. 357 (6377): 390–391. Bibcode:1992Natur.357..390K. doi:10.1038/357390a0. S2CID 37062511.
- ↑ Physorg.com, "New Way of 'Seeing': A 'Neutron Microscope'" Archived 2012-01-24 at the Wayback Machine. Physorg.com (2004-07-30). Retrieved on 2012-08-16.
- ↑ "NASA Develops a Nugget to Search for Life in Space" Archived 2014-03-08 at the Wayback Machine. NASA.gov (2007-11-30). Retrieved on 2012-08-16.
- ↑ Ioffe, A.; Dabagov, S.; Kumakhov, M. (1995-01-01). "Effective neutron bending at large angles". Neutron News. 6 (3): 20–21. doi:10.1080/10448639508217696. ISSN 1044-8632.
- ↑ Hall, Eric J. (2000). Radiobiology for the radiologist (5th ed.). Philadelphia: Lippincott Williams & Wilkins. ISBN 0-7817-2649-2. OCLC 43854159.
- ↑ Johns HE and Cunningham JR (1978). The Physics of Radiology. Charles C Thomas 3rd edition
- ↑ brian.maranville@nist.gov (2017-04-17). "How neutrons are useful". NIST. Archived from the original on 2021-01-25. Retrieved 2021-01-21.
- ↑ E Hadden; Y Iso; A Kume; K Umemoto; T Jenke; M Fally; J Klepp; Y Tomita (2022). "Highly efficient holographic optical elements for cold neutron experiments". ResearchGate. doi:10.13140/RG.2.2.26033.04963.
- ↑ Hadden, Elhoucine; Iso, Yuko; Kume, Atsushi; Umemoto, Koichi; Jenke, Tobias; Fally, Martin; Klepp, Jürgen; Tomita, Yasuo (2022-05-24). "Nanodiamond-based nanoparticle-polymer composite gratings with extremely large neutron refractive index modulation". In McLeod, Robert R; Tomita, Yasuo; Sheridan, John T; Pascual Villalobos, Inmaculada (eds.). Photosensitive Materials and their Applications II. Vol. 12151. SPIE. pp. 70–76. Bibcode:2022SPIE12151E..09H. doi:10.1117/12.2623661. ISBN 9781510651784. S2CID 249056691.
- ↑ B. Lauss (May 2012). "Startup of the high-intensity ultracold neutron source at the Paul Scherrer Institute". Hyperfine Interact. 211 (1): 21–25. arXiv:1202.6003. Bibcode:2012HyInt.211...21L. doi:10.1007/s10751-012-0578-7. S2CID 119164071.
- ↑ R. Golub & J. M. Pendlebury (1977). "The interaction of Ultra-Cold Neutrons (UCN) with liquid helium and a superthermal UCN source". Phys. Lett. A. 62 (5): 337–339. Bibcode:1977PhLA...62..337G. doi:10.1016/0375-9601(77)90434-0.
- ↑ A. Steyerl; H. Nagel; F.-X. Schreiber; K.-A. Steinhauser; R. Gähler; W. Gläser; P. Ageron; J. M. Astruc; W. Drexel; G. Gervais & W. Mampe (1986). "A new source of cold and ultracold neutrons". Phys. Lett. A. 116 (7): 347–352. Bibcode:1986PhLA..116..347S. doi:10.1016/0375-9601(86)90587-6.
- ↑ Stefan Döge; Jürgen Hingerl & Christoph Morkel (Feb 2020). "Measured velocity spectra and neutron densities of the PF2 ultracold-neutron beam ports at the Institut Laue–Langevin". Nucl. Instrum. Methods A. 953: 163112. arXiv:2001.04538. Bibcode:2020NIMPA.95363112D. doi:10.1016/j.nima.2019.163112. S2CID 209942845. Archived from the original on 2021-02-24. Retrieved 2020-04-24.
- ↑ Freeman, Tami (May 23, 2008). "Facing up to secondary neutrons". Medical Physics Web. Archived from the original on 2010-12-20. Retrieved 2011-02-08.
- ↑ Heilbronn, L.; Nakamura, T; Iwata, Y; Kurosawa, T; Iwase, H; Townsend, LW (2005). "Expand+Overview of secondary neutron production relevant to shielding in space". Radiation Protection Dosimetry. 116 (1–4): 140–143. doi:10.1093/rpd/nci033. PMID 16604615. Archived from the original on 2019-01-26. Retrieved 2019-01-25.
Further reading
- James Byrne, Neutrons, Nuclei and Matter: An Exploration of the Physics of Slow Neutrons. Mineola, New York: Dover Publications, 2011. ISBN 0486482383.
- Abraham Pais, Inward Bound, Oxford: Oxford University Press, 1986. ISBN 0198519974.
- Sin-Itiro Tomonaga, The Story of Spin, The University of Chicago Press, 1997
- Herwig Schopper, Weak interactions and nuclear beta decay, Publisher, North-Holland Pub. Co., 1966.
- Annotated bibliography for neutrons from the Alsos Digital Library for Nuclear Issues