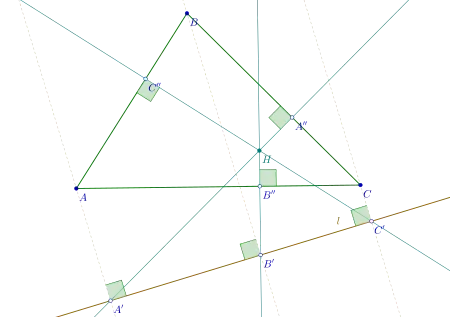
In geometry, the orthopole of a system consisting of a triangle ABC and a line ℓ in the same plane is a point determined as follows.[1] Let A ′, B ′, C ′ be the feet of perpendiculars dropped on ℓ from A, B, C respectively. Let A ′′, B ′′, C ′′ be the feet of perpendiculars dropped from A ′, B ′, C ′ to the sides opposite A, B, C (respectively) or to those sides' extensions. Then the three lines A ′ A ′′, B ′ B ′′, C ′ C ′′, are concurrent.[2] The point at which they concur is the orthopole.
Due to their many properties,[3] orthopoles have been the subject of a large literature.[4] Some key topics are determination of the lines having a given orthopole[5] and orthopolar circles.[6]
Literature
References
- ↑ "MathWorld: Orthopole".
- ↑ Goormaghtigh, R. (1926). "The Orthopole". Tohoku Mathematical Journal. First Series. 27: 77–125.
- ↑ "The Orthopole". 21 January 2017.
- ↑ Ramler, O. J. (1930). "The Orthopole Loci of Some One-Parameter Systems of Lines Referred to a Fixed Triangle". The American Mathematical Monthly. 37 (3): 130–136. doi:10.2307/2299415. JSTOR 2299415.
- ↑ Karl, Mary Cordia (1932). "The Projective Theory of Orthopoles". The American Mathematical Monthly. 39 (6): 327–338. doi:10.2307/2300757. JSTOR 2300757.
- ↑ Goormaghtigh, R. (December 1946). "1936. The orthopole". The Mathematical Gazette. 30 (292): 293. doi:10.2307/3610737. JSTOR 3610737. S2CID 185932136.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.