In mathematics, the projective special linear group PSL(2, 7), isomorphic to GL(3, 2), is a finite simple group that has important applications in algebra, geometry, and number theory. It is the automorphism group of the Klein quartic as well as the symmetry group of the Fano plane. With 168 elements, PSL(2, 7) is the smallest nonabelian simple group after the alternating group A5 with 60 elements, isomorphic to PSL(2, 5).
Definition
The general linear group GL(2, 7) consists of all invertible 2×2 matrices over F7, the finite field with 7 elements. These have nonzero determinant. The subgroup SL(2, 7) consists of all such matrices with unit determinant. Then PSL(2, 7) is defined to be the quotient group
- SL(2, 7) / {I, −I}
obtained by identifying I and −I, where I is the identity matrix. In this article, we let G denote any group isomorphic to PSL(2, 7).
Properties
G = PSL(2, 7) has 168 elements. This can be seen by counting the possible columns; there are 72 − 1 = 48 possibilities for the first column, then 72 − 7 = 42 possibilities for the second column. We must divide by 7 − 1 = 6 to force the determinant equal to one, and then we must divide by 2 when we identify I and −I. The result is (48 × 42) / (6 × 2) = 168.
It is a general result that PSL(n, q) is simple for n, q ≥ 2 (q being some power of a prime number), unless (n, q) = (2, 2) or (2, 3). PSL(2, 2) is isomorphic to the symmetric group S3, and PSL(2, 3) is isomorphic to alternating group A4. In fact, PSL(2, 7) is the second smallest nonabelian simple group, after the alternating group A5 = PSL(2, 5) = PSL(2, 4).
The number of conjugacy classes and irreducible representations is 6. The sizes of conjugacy classes are 1, 21, 42, 56, 24, 24. The dimensions of irreducible representations 1, 3, 3, 6, 7, 8.
Character table
where:
The following table describes the conjugacy classes in terms of the order of an element in the class, the size of the class, the minimum polynomial of every representative in GL(3, 2), and the function notation for a representative in PSL(2, 7). Note that the classes 7A and 7B are exchanged by an automorphism, so the representatives from GL(3, 2) and PSL(2, 7) can be switched arbitrarily.
| Order | Size | Min Poly | Function |
|---|---|---|---|
| 1 | 1 | x + 1 | x |
| 2 | 21 | x2 + 1 | −1/x |
| 3 | 56 | x3 + 1 | 2x |
| 4 | 42 | x3 + x2 + x + 1 | 1/(3 − x) |
| 7 | 24 | x3 + x+1 | x + 1 |
| 7 | 24 | x3 + x2 + 1 | x + 3 |
The order of group is 168 = 3 × 7 × 8, this implies existence of Sylow's subgroups of orders 3, 7 and 8. It is easy to describe the first two, they are cyclic, since any group of prime order is cyclic. Any element of conjugacy class 3A56 generates Sylow 3-subgroup. Any element from the conjugacy classes 7A24, 7B24 generates the Sylow 7-subgroup. The Sylow 2-subgroup is a dihedral group of order 8. It can be described as centralizer of any element from the conjugacy class 2A21. In the GL(3, 2) representation, a Sylow 2-subgroup consists of the upper triangular matrices.
This group and its Sylow 2-subgroup provide a counter-example for various normal p-complement theorems for p = 2.
Actions on projective spaces
G = PSL(2, 7) acts via linear fractional transformation on the projective line P1(7) over the field with 7 elements:
Every orientation-preserving automorphism of P1(7) arises in this way, and so G = PSL(2, 7) can be thought of geometrically as a group of symmetries of the projective line P1(7); the full group of possibly orientation-reversing projective linear automorphisms is instead the order 2 extension PGL(2, 7), and the group of collineations of the projective line is the complete symmetric group of the points.
However, PSL(2, 7) is also isomorphic to PSL(3, 2) (= SL(3, 2) = GL(3, 2)), the special (general) linear group of 3×3 matrices over the field with 2 elements. In a similar fashion, G = PSL(3, 2) acts on the projective plane P2(2) over the field with 2 elements — also known as the Fano plane:
- For and
Again, every automorphism of P2(2) arises in this way, and so G = PSL(3, 2) can be thought of geometrically as the symmetry group of this projective plane. The Fano plane can be used to describe multiplication of octonions, so G acts on the set of octonion multiplication tables.
Symmetries of the Klein quartic
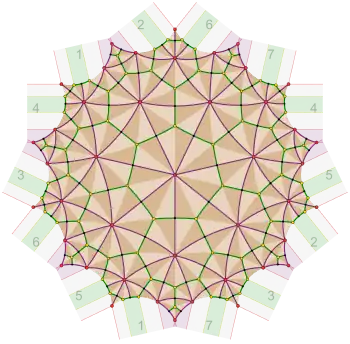
The Klein quartic is the projective variety over the complex numbers C defined by the quartic polynomial
- x3y + y3z + z3x = 0.
It is a compact Riemann surface of genus g = 3, and is the only such surface for which the size of the conformal automorphism group attains the maximum of 84(g−1). This bound is due to the Hurwitz automorphisms theorem, which holds for all g>1. Such "Hurwitz surfaces" are rare; the next genus for which any exist is g = 7, and the next after that is g = 14.
As with all Hurwitz surfaces, the Klein quartic can be given a metric of constant negative curvature and then tiled with regular (hyperbolic) heptagons, as a quotient of the order-3 heptagonal tiling, with the symmetries of the surface as a Riemannian surface or algebraic curve exactly the same as the symmetries of the tiling. For the Klein quartic this yields a tiling by 24 heptagons, and the order of G is thus related to the fact that 24 × 7 = 168. Dually, it can be tiled with 56 equilateral triangles, with 24 vertices, each of degree 7, as a quotient of the order-7 triangular tiling.
Klein's quartic arises in many fields of mathematics, including representation theory, homology theory, octonion multiplication, Fermat's Last Theorem, and Stark's theorem on imaginary quadratic number fields of class number 1.
Mathieu group
PSL(2, 7) is a maximal subgroup of the Mathieu group M21; the groups M21 and M24 can be constructed as extensions of PSL(2, 7). These extensions can be interpreted in terms of the tiling of the Klein quartic, but are not realized by geometric symmetries of the tiling.[1]
Permutation actions
The group PSL(2, 7) acts on various finite sets:
- In its original interpretation as PSL(2, 7), orientation-preserving linear automorphisms of the projective line P1(F7), it acts transitively on the 8 points with a stabilizer of order 21 fixing a given point. It also acts 2-transitively with stabilizer of order 3 on each pair of points; and it has two orbits on triples of points, with trivial stabilizer on each triple. (The larger group PGL(2, 7) acts sharply 3-transitively.)
- Interpreted as PGL(3, 2), linear automorphisms of the Fano plane P2(F2), it acts 2-transitively on the 7 points, with stabilizer of order 24 fixing each point, and stabilizer of order 4 fixing each pair of points.
- Interpreted as automorphisms of a tiling of the Klein quartic, it acts transitively on the 24 vertices (or dually, 24 heptagons), with stabilizer of order 7 (corresponding to a rotation about the vertex/heptagon).
- Interpreted as a subgroup of the Mathieu group M21, the subgroup acts non-transitively on 21 points.
References
- Richter, David A., How to Make the Mathieu Group M24, retrieved 2010-04-15
Further reading
- Brown, Ezra; Loehr, Nicholas (2009). "Why is PSL (2,7)≅ GL (3,2)?" (PDF). Am. Math. Mon. 116 (8): 727–732. doi:10.4169/193009709X460859. Zbl 1229.20046. Archived from the original (PDF) on 2016-10-09. Retrieved 2014-09-27.