Heliospheric current sheet

The heliospheric current sheet, or interplanetary current sheet, is a surface separating regions of the heliosphere where the interplanetary magnetic field points toward and away from the Sun.[1] A small electrical current with a current density of about 10−10 A/m2 flows within this surface, forming a current sheet confined to this surface.[2][3][4] The shape of the current sheet results from the influence of the Sun's rotating magnetic field on the plasma in the interplanetary medium.[5] The thickness of the current sheet is about 10,000 km (6,200 mi) near the orbit of the Earth.

Characteristics

Ballerina's skirt shape

The Parker Spiral

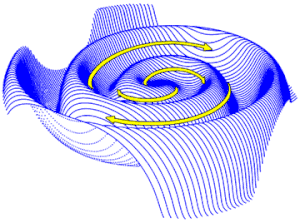
As the Sun rotates, its magnetic field twists into an Archimedean spiral, as it extends through the Solar System. This phenomenon is often called the Parker spiral, after Eugene Parker's work[6] that predicted the structure of the interplanetary magnetic field. The spiral nature of the heliospheric magnetic field was noted earlier by Hannes Alfvén,[7] based on the structure of comet tails.

The influence of this spiral-shaped magnetic field on the interplanetary medium (solar wind) creates the largest structure in the Solar System, the heliospheric current sheet. Parker's spiral magnetic field was divided in two by a current sheet,[8] a mathematical model first developed in the early 1970s by Schatten. It warps into a wavy spiral shape that has been likened to a ballerina's skirt.[9][10] The waviness of the current sheet is due to the magnetic field dipole axis' tilt angle to the solar rotation axis and variations from an ideal dipole field.[11]

Unlike the familiar shape of the field from a bar magnet, the Sun's extended field is twisted into an arithmetic spiral by the magnetohydrodynamic influence of the solar wind. The solar wind travels outward from the Sun at a rate of 200-800km/s, but an individual jet of solar wind from a particular feature on the Sun's surface rotates with the solar rotation, making a spiral pattern in space. The cause of this ballerina spiral shape has sometimes been called the "garden sprinkler effect" or "garden hose effect",[12][13] because it is likened to a lawn sprinkler with nozzle that moves up and down while it spins; the stream of water represents the solar wind. Unlike the jet from a sprinkler, however, the solar wind is tied to the magnetic field by MHD effects, so that magnetic field lines are tied to the material in the jet and take on an arithmetic spiral shape.

The Parker spiral shape of the solar wind changes the shape of the Sun's magnetic field in the outer Solar System: beyond about 10–20 astronomical units from the Sun, the magnetic field is nearly toroidal (pointed around the equator of the Sun) rather than poloidal (pointed from the North to the South pole, as in a bar magnet) or radial (pointed outward or inward, as might be expected from the flow of the solar wind if the Sun were not rotating). The spiral shape also greatly amplifies the strength of the solar magnetic field in the outer Solar System.

The Parker spiral may be responsible for the differential solar rotation, in which the Sun's poles rotate more slowly (about a 35-day rotation period) than the equator (about a 27-day rotation period). The solar wind is guided by the Sun's magnetic field and hence largely emanates from the polar regions of the Sun; the induced spiral shape of the field causes a drag torque on the poles due to the magnetic tension force.

During solar maximum the entire magnetic field of the Sun flips, thus alternating the polarity of the field every solar cycle.[14]

Magnetic field

The heliospheric current sheet rotates along with the Sun with a period of about 25 days, during which time the peaks and troughs of the skirt pass through the Earth's magnetosphere, interacting with it. Near the surface of the Sun, the magnetic field produced by the radial electric current in the sheet is of the order of 5×10−6 T.[2]

The magnetic field at the surface of the Sun is about 10−4 T. If the form of the field were a magnetic dipole, the strength would decrease with the cube of the distance, resulting in about 10−11 T at the Earth's orbit. The heliospheric current sheet results in higher order multipole components so that the actual magnetic field at the Earth due to the Sun is 100 times greater.

Electric current

The electric current in the heliospheric current sheet has a radial component (directed inward) as well as an azimuthal component, the radial circuit being closed by outward currents aligned with the Sun's magnetic field in the solar polar regions. The radial current in the circuit is on the order of 3×109 amperes.[2] As a comparison with other astrophysical electric currents, the Birkeland currents that supply the Earth's aurora are about a thousand times weaker at a million amperes. The maximum current density in the sheet is on the order of 10−10 A/m2 (10−4 A/km2).

History

The heliospheric current sheet was discovered by John M. Wilcox and Norman F. Ness, who published their finding in 1965.[15] Hannes Alfvén and Per Carlqvist speculate on the existence of a galactic current sheet, a counterpart of the heliospheric current sheet, with an estimated galactic current of 1017 to 1019 amperes, that might flow in the plane of symmetry of the galaxy.[16]

References

  1. ↑ "The heliospheric current sheet" Smith, E. J, Journal of Geophysical Research 106, A8, 15819, 2001.
  2. 1 2 3 Israelevich, P. L., et al., "MHD simulation of the three-dimensional structure of the heliospheric current sheet Archived 2017-03-23 at the Wayback Machine" (2001) Astronomy and Astrophysics, v.376, p.288–291
  3. ↑ A Star with two North Poles Archived 2009-07-18 at the Wayback Machine, April 22, 2003, Science @ NASA
  4. ↑ Riley, Pete; Linker, J. A.; Mikić, Z., "Modeling the heliospheric current sheet: Solar cycle variations", (2002) Journal of Geophysical Research (Space Physics), Volume 107, Issue A7, pp. SSH 8-1, CiteID 1136, DOI 10.1029/2001JA000299. (Full text Archived 2009-08-14 at the Wayback Machine)
  5. ↑ "Artist's Conception of the Heliospheric Current Sheet". Archived from the original on September 1, 2006. Retrieved 2005-11-20.{{cite web}}: CS1 maint: bot: original URL status unknown (link)
  6. ↑ Parker, E. N., "Dynamics of the Interplanetary Gas and Magnetic Fields", (1958) Astrophysical Journal, vol. 128, p.664
  7. ↑ "On the theory of comet tails", H. Alfvén, Tellus 9, 92, 1957.
  8. ↑ "Current Sheet Magnetic Model for the Solar Corona", K. H. Schatten, Cosmic Electrodynamics, 2, 232–245, 1971.
  9. ↑ Rosenberg, R. L. and P. J. Coleman, Jr., Heliographic latitude dependence of the dominant polarity of the interplanetary magnetic field, J. Geophys. Res., 74 (24), 5611–5622, 1969.
  10. ↑ Wilcox, J. M.; Scherrer, P. H.; Hoeksema, J. T., "The origin of the warped heliospheric current sheet" (1980)
  11. ↑ Owens, M. J.; Forsyth, R. J. (2013). "The Heliospheric Magnetic Field". Living Reviews in Solar Physics. 10 (1): 11. arXiv:1002.2934. Bibcode:2013LRSP...10....5O. doi:10.12942/lrsp-2013-5. S2CID 122870891.
  12. ↑ Louise K. Harra, Keith O. Mason, Space Science 2004, Imperial College Press, ISBN 1-86094-361-6
  13. ↑ Smith, E., "The Sun, Solar Wind, and Magnetic Field Archived 2008-02-05 at the Wayback Machine", Jul 1999, Proceedings of the International School of Physics Enrico FERMI Varenna, Italy
  14. ↑ Barbier, Beth. "NASA's Cosmicopia – Sun – Sun's Magnetic Field". Archived from the original on 1998-12-02.
  15. ↑ Wilcox, John M.; Ness, Norman F. (1965). "Quasi-Stationary Corotating Structure in the Interplanetary Medium". Journal of Geophysical Research. 70 (23): 5793–5805. Bibcode:1965JGR....70.5793W. doi:10.1029/JZ070i023p05793. hdl:2060/19660001924. S2CID 121122792.
  16. ↑ Alfvén, Hannes; Carlqvist, Per (1978). "Interstellar clouds and the formation of stars". Astrophysics and Space Science. 55 (2): 487–509. Bibcode:1978Ap&SS..55..487A. doi:10.1007/bf00642272. S2CID 122687137.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.