Photon-counting computed tomography (PCCT) is a form of X-ray computed tomography (CT) in which X-rays are detected using a photon-counting detector (PCD) which registers the interactions of individual photons. By keeping track of the deposited energy in each interaction, the detector pixels of a PCD each record an approximate energy spectrum, making it a spectral or energy-resolved CT technique. In contrast, more conventional CT scanners use energy-integrating detectors (EIDs), where the total energy (generally from a large number of photons as well as electronic noise) deposited in a pixel during a fixed period of time is registered. These EIDs thus register only photon intensity, comparable to black-and-white photography, whereas PCDs register also spectral information, similar to color photography.
The first clinically-approved PCCT system was cleared by the Food and Drug Administration (FDA) in September 2021.[1]
General advantages
Often EIDs are used as a baseline for comparison when evaluating PCD performance capabilities. With this lens, there are several potential advantages of using a PCD over using an EID in CT imaging. These include improved signal (and contrast) to noise ratio, reduced X-ray dose to the patient, improved spatial resolution and, through use of several energy bins, the ability to distinguish multiple contrast agents.[2][3] Due to the large volumes and rates of data required (up to several hundred million photon interactions per mm2 and second[4]) the use of PCDs in CT scanners has become feasible only with recent improvements in detector technology. As of January 2021 photon-counting CT is in use at five clinical sites.[5][6][7][8] Some early research has found the dose reduction potential of photon-counting CT for breast imaging to be very promising.[9] On September 29, 2021 the FDA cleared the first photon-counting CT (developed by Siemens Healthineers) for clinical use.[1]
Detection characteristics
Discrete energy-dependent detection
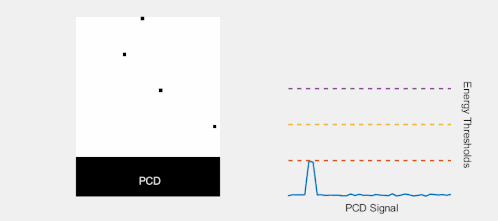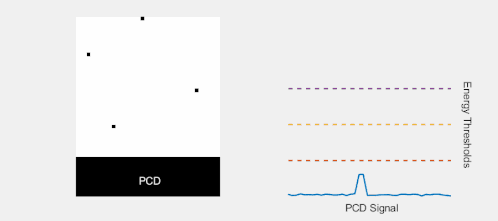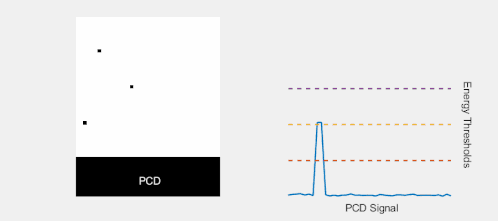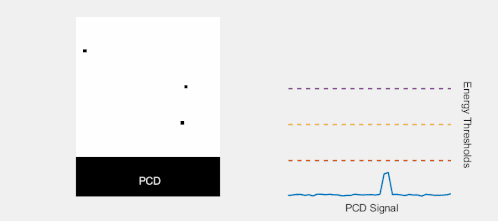
When a photon interacts in a PCD, the amplitude of the resulting electrical pulse is roughly proportional to the photon energy. By comparing each pulse produced in a pixel with a suitable low-energy threshold, contributions from low-energy events (resulting from both photon interactions and electronic noise) can be filtered out. This effectively eliminates contributions from electronic noise at the expense of discarding photons with energy comparable to the noise level (which are of little use since they are indistinguishable from noise counts). In an EID, on the other hand, the contributions from individual photons are not known. Therefore, an energy threshold cannot be applied, making this technique susceptible to noise and other factors which can affect the linearity of the voltage to X-ray intensity relationship.[10]
The removal of electronic noise gives PCDs two advantages over EIDs. First, higher signal-to-noise and contrast-to-noise ratios are expected from using PCDs compared to EIDs. This can either be used to increase the image quality at the same X-ray exposure level, or to lower the patient X-ray dose whilst maintaining the same image quality. Second, it is difficult to manufacture energy-integrating detectors with smaller pixel size than approximately 1×1 mm2 without compromising dose efficiency. The reason for this is that reflective layers must be placed in the scintillator between the pixels to prevent cross-talk between pixels, and these cannot be made too thin. In addition, the measured signal is proportional to the pixel area whereas the electronic noise is fairly independent of pixel size, so that noise will dominate the measured signal if the pixels are made too small. These problems do not occur in a photon-counting detector with a low-energy threshold, which can therefore achieve higher detector resolution.
Multi-energy, spectral detection
By introducing more energy thresholds above the low-energy threshold, a PCD can be divided into several discrete energy bins. Each registered photon is thus assigned to a specific bin depending on its energy, such that each pixel measures a histogram of the incident X-ray spectrum. This spectral information provides several advantages over the integrated deposited energy of an EID.[2] First, it makes it possible to quantitatively determine the material composition of each pixel in the reconstructed CT image, as opposed to the estimated average linear attenuation coefficient obtained in a conventional CT scan. It turns out such a material base decomposition, using at least two energy bins, can adequately account for all elements found in the body and increases the contrast between tissue types.[11] Further, the spectral information can be used to remove beam hardening artefacts. These arise because of the higher linear attenuation of most materials at lower energy which shifts the mean energy of the X-ray spectrum towards higher energies as the beam passes through the object. By comparing the ratios of counts in different energy bins with those of the attenuated beam, the amount of beam hardening can be accounted for (either explicitly or implicitly in the reconstruction) using a PCD. Finally, using more than two energy bins allows to discriminate between on the one hand dense bone and calcifications and on the other hand heavier elements (commonly iodine or gadolinium) used as contrast agents. This has the potential reduce the amount of X-ray dose from a contrast scan by removing the need for a reference scan before contrast injection. Although spectral CT is already clinically available in the form of dual-energy scanners, photon-counting CT offers a number of advantages. A PCD can implement more than two energy thresholds with a higher degree of separation than what is possible to achieve in dual-energy CT. This improvement in energy resolution translates to higher contrast-to-noise ratio in the image, in particular in contrast-enhanced and material-selective images. Also, it can be shown that at least three energies are necessary to simultaneously decompose both tissue and contrast medium.[12] More energy bins also allow for simultaneously differentiating between different contrast agents.[13]
Detection challenges and spectral distortion
Despite encouraging research, there are several challenges which have until recently prevented incorporating PCDs in CT systems. Many challenges are related to demands on detector material and electronics resulting from large data volumes and count rates. As an example, each mm2 of a CT detector may receive several hundred million photon interactions per second during a scan.[4]
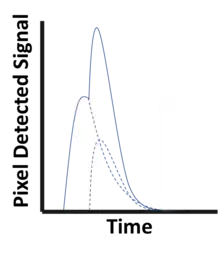
To avoid saturation in areas where little material is present between the X-ray source and the detector, the pulse resolving time must be small compared to the average time between photon interactions in a pixel. Even before saturation, the detector functionality starts to deteriorate because of pulse pileup (see figure to the left), where two (or more) photon interactions take place in the same pixel too close in time to be resolved as discrete events. Such quasi-coincident interactions lead to a loss of photon counts and distorts the pulse shape, skewing the recorded energy spectrum.[2] Due to these effects, the demands on the physical response time of the detector material as well as on the electronics responsible for pulse-shaping, binning and recording pixel data become very high. Using smaller image pixels decreases the per-pixel count rate and thus alleviates the demands on pulse resolving time at the expense of requiring more electronics.
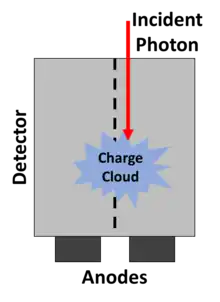
Partial energy deposition and single photons causing signals in multiple pixels poses another challenge in photon-counting CT.[2] Charge sharing, where an interaction takes place close to a pixel boundary, causing the released energy to be shared between neighboring pixels and thus be interpreted as several lower-energy photons, is one cause of such events (see figure to the right). Others include the emission of K-escape X-rays and Compton scattering, where the escaping or scattered photon results in a partial energy deposition in the primary pixel and may go on to cause further interactions in different pixels. The effects mentioned take place also in EIDs but cause additional problems in PCDs since they result in a distorted energy spectrum. In contrast to saturation and pileup effects, problems caused by partial energy deposition and multiply interacting photons is aggravated by smaller pixel size. Anti-coincidence logic, where simultaneous events in nearby pixels are added, can be used to somewhat counteract counting the same photon in different pixels.
Image reconstruction
Classical CT reconstruction
The fundamental challenge of tomographic reconstruction is the inverse problem of reconstructing the 3D, tomographic information of a volume using 2D projections from different angular positions. The same fundamental methods conventionally used for tomographic reconstruction can be used without alteration on data acquired from PCDs.[2] The fundamental geometric, physical, and mathematical approaches to typical reconstruction are unchanged by this new detection method. Arguably the most fundamental method of CT image reconstruction is filtered back projection. More in depth operations and the wide selection of iterative reconstruction methods remain entirely applicable. There is a great deal of literature on CT reconstruction for curious readers.[14]
Multi-energy reconstruction
Access to multiple energy bins opens up new possibilities when it comes to reconstructing a CT image from the acquired projections. The most basic possibility is to treat each of the N energy bins separately and use a conventional CT reconstruction method to reconstruct N different images.[15]
Material decomposition
As a next step to a multi-energy reconstruction, it is possible to determine the material components at a given voxel location by comparing and/or combining the intensities of the N images at this location. This is typically performed by writing each pixel as a linear combination of M base materials of known properties such as water, calcium, and a contrast agent such as iodine. This method is referred to as image-based material decomposition. Although intuitive, this pixel-wise approach relies heavily on the spectral fidelity (or spectral calibration) of the individual detector pixels across thresholds and does nothing to remove common image artifacts.
Another option is to perform the material base decomposition directly on the projection data, before the reconstruction. Using projection-based material decomposition, the material composition measured by a detector pixel for a given projection is expressed as a linear combination of M basis materials (e.g. soft tissue, bone and contrast agent). This is determined from the recorded energy histogram, for example through maximum likelihood estimation.[12] The reconstruction is then performed separately for each material basis, yielding M reconstructed basis images.
A third option would be to employ a single-step reconstruction, where the material basis decomposition is performed simultaneously with the image reconstruction. This approach, however, is not compatible with the reconstruction algorithms used in current clinical CT systems. Instead, novel iterative algorithms specific to photon-counting CT are required.
Research in the field of deep learning has also introduced possibilities of performing material decomposition using convolutional neural networks.[16]
Detector composition
Experimental PCDs for use in CT systems use semiconductor detectors based on either cadmium (zinc) telluride or silicon, neither of which need cryogenic cooling to operate. Cadmium telluride and cadmium zinc telluride detectors have the advantage of high attenuation and relatively high photoelectric-to-Compton ratio for X-ray energies used in CT imaging. This means the detectors can be made thinner and lose less spectral information due to Compton scattering. (Although they still lose spectral information due to K-escape electrons.) However, detectors made of Cadmium telluride (zinc) have longer collection times due to low charge carrier mobility, and thus suffer more from pileup effects. Further, it is currently difficult to produce such crystals without defects and impurities, which cause detector polarisation and incomplete charge collection.[17]
Silicon detectors, on the other hand, are more easily manufactured and less prone to pileup due to high charge carrier mobility. They do not suffer from K-escape X-rays but have a lower photoelectric-to-Compton ratio at X-ray energies used in CT imaging, which degrades the collected energy spectrum. Further, silicon attenuates X-rays less strongly and therefore silicon detectors have to be several centimetres thick to be useful in a CT system.[17]
References
- 1 2 "FDA Clears First Major Imaging Device Advancement for Computed Tomography in Nearly a Decade". Food and Drug Administration. 30 September 2021.
- 1 2 3 4 5 Taguchi K, Iwanczyk JS (October 2013). "Vision 20/20: Single photon counting x-ray detectors in medical imaging". Medical Physics. 40 (10): 100901. Bibcode:2013MedPh..40j0901T. doi:10.1118/1.4820371. PMC 3786515. PMID 24089889.
- ↑ Shikhaliev PM, Xu T, Molloi S (February 2005). "Photon counting computed tomography: concept and initial results". Medical Physics. 32 (2): 427–36. Bibcode:2005MedPh..32..427S. doi:10.1118/1.1854779. PMID 15789589.
- 1 2 Persson M, Bujila R, Nowik P, Andersson H, Kull L, Andersson J, Bornefalk H, Danielsson M (July 2016). "Upper limits of the photon fluence rate on CT detectors: Case study on a commercial scanner". Medical Physics. 43 (7): 4398–4411. Bibcode:2016MedPh..43.4398P. doi:10.1118/1.4954008. PMID 27370155.
- ↑ "NIH uses photon-counting CT scanner in patients for the first time". National Institutes of Health (NIH). 2016-02-24. Retrieved 2017-11-22.
- ↑ "CT Clinical Innovation Center: four decades of CT innovation at Mayo Clinic". Mayo Clinic Alumni Association. Retrieved 2021-01-19.
- ↑ "Unique research photon-counting CT scanner to CMIV". liu.se. Retrieved 2021-01-19.
- ↑ "Schärfere Augen für die Computertomographie: Mit Photon-Counting Metastasen besser beurteilen". Radiologie Magazin (in German). 2021-01-11. Retrieved 2021-01-19.
- ↑ Kalender WA, Kolditz D, Steiding C, Ruth V, Lück F, Rößler AC, Wenkel E (March 2017). "Technical feasibility proof for high-resolution low-dose photon-counting CT of the breast". European Radiology. 27 (3): 1081–1086. doi:10.1007/s00330-016-4459-3. PMID 27306559. S2CID 7912239.
- ↑ Jenkins R, Gould RW, Gedcke D (1995). Quantitative x-ray spectrometry (2nd ed.). New York: Dekker. p. 90. ISBN 9780824795542. OCLC 31970216.
- ↑ Alvarez RE, Macovski A (1976). "Energy-selective reconstructions in X-ray computerized tomography". Physics in Medicine and Biology. 21 (5): 733–44. Bibcode:1976PMB....21..733A. doi:10.1088/0031-9155/21/5/002. PMID 967922. S2CID 250824716.
- 1 2 Roessl E, Proksa R (August 2007). "K-edge imaging in x-ray computed tomography using multi-bin photon counting detectors". Physics in Medicine and Biology. 52 (15): 4679–96. doi:10.1088/0031-9155/52/15/020. PMID 17634657. S2CID 5871406.
- ↑ Schlomka JP, Roessl E, Dorscheid R, Dill S, Martens G, Istel T, Bäumer C, Herrmann C, Steadman R, Zeitler G, Livne A, Proksa R (August 2008). "Experimental feasibility of multi-energy photon-counting K-edge imaging in pre-clinical computed tomography". Physics in Medicine and Biology. 53 (15): 4031–47. Bibcode:2008PMB....53.4031S. doi:10.1088/0031-9155/53/15/002. PMID 18612175. S2CID 25238021.
- ↑ Pan, Xiaochuan; Sidky, Emil Y; Vannier, Michael (2009-12-01). "Why do commercial CT scanners still employ traditional, filtered back-projection for image reconstruction?". Inverse Problems. 25 (12): 123009. doi:10.1088/0266-5611/25/12/123009. ISSN 0266-5611. PMC 2849113. PMID 20376330.
- ↑ Schmidt TG (July 2009). "Optimal "image-based" weighting for energy-resolved CT". Medical Physics. 36 (7): 3018–27. Bibcode:2009MedPh..36.3018S. doi:10.1118/1.3148535. PMID 19673201.
- ↑ Gong, Hao; Tao, Shengzhen; Rajendran, Kishore; Zhou, Wei; McCollough, Cynthia H.; Leng, Shuai (December 2020). "Deep‐learning‐based direct inversion for material decomposition". Medical Physics. 47 (12): 6294–6309. Bibcode:2020MedPh..47.6294G. doi:10.1002/mp.14523. ISSN 0094-2405. PMC 7796910. PMID 33020942.
- 1 2 Persson M, Huber B, Karlsson S, Liu X, Chen H, Xu C, Yveborg M, Bornefalk H, Danielsson M (November 2014). "Energy-resolved CT imaging with a photon-counting silicon-strip detector". Physics in Medicine and Biology. 59 (22): 6709–27. Bibcode:2014PMB....59.6709P. doi:10.1088/0022-3727/59/22/6709. PMID 25327497.