
Orthographic projections and Schlegel diagrams with Hamiltonian cycles of the vertices of the five platonic solids – only the octahedron has an Eulerian path or cycle, by extending its path with the dotted one

The platonic graphs can be seen as Schlegel diagrams of the platonic solids. (excluding the square pyramid also shown here)
In the mathematical field of graph theory, a Platonic graph is a graph that has one of the Platonic solids as its skeleton. There are 5 Platonic graphs, and all of them are regular, polyhedral (and therefore by necessity also 3-vertex-connected, vertex-transitive, edge-transitive and planar graphs), and also Hamiltonian graphs.[1]
- Tetrahedral graph – 4 vertices, 6 edges
- Octahedral graph – 6 vertices, 12 edges
- Cubical graph – 8 vertices, 12 edges
- Icosahedral graph – 12 vertices, 30 edges
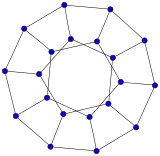
- Dodecahedral graph – 20 vertices, 30 edges
 |
 |
 |
 |
 |
See also
References
- ↑ Read, R. C. and Wilson, R. J. An Atlas of Graphs, Oxford, England: Oxford University Press, 2004 reprint, Chapter 6 special graphs pp. 261, 266.
External links
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.