A Poincaré plot, named after Henri Poincaré, is a type of recurrence plot used to quantify self-similarity in processes, usually periodic functions. It is also known as a return map.[1][2] Poincaré plots can be used to distinguish chaos from randomness by embedding a data set in a higher-dimensional state space.

Given a time series of the form

a return map in its simplest form first plots (xt, xt+1), then plots (xt+1, xt+2), then (xt+2, xt+3), and so on.

Applications in electrocardiography

An electrocardiogram (ECG) is a tracing of the voltage changes in the chest generated by the heart, whose contraction in a normal person is triggered by an electrical impulse that originates in the sinoatrial node. The ECG normally consists of a series of waves, labeled the P, Q, R, S and T waves. The P wave represents depolarization of the atria, the Q-R-S series of waves depolarization of the ventricles and the T wave repolarization of the ventricles. The interval between two successive R waves (the RR interval) is a measure of the heart rate.

The heart rate normally varies slightly: during a deep breath, it speeds up and during a deep exhalation, it slows down. (The RR interval will shorten when the heart speeds up, and lengthen when it slows.) An RR tachograph is a graph of the numerical value of the RR-interval versus time.

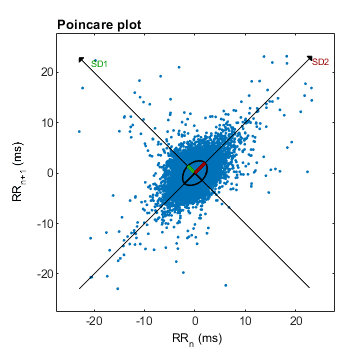
In the context of RR tachography, a Poincaré plot is a graph of RR(n) on the x-axis versus RR(n + 1) (the succeeding RR interval) on the y-axis, i.e. one takes a sequence of intervals and plots each interval against the following interval.[3] The recurrence plot is used as a standard visualizing technique to detect the presence of oscillations in non-linear dynamic systems. In the context of electrocardiography, the rate of the healthy heart is normally tightly controlled by the body's regulatory mechanisms (specifically, by the autonomic nervous system). Several research papers[4][5] demonstrate the potential of ECG signal-based Poincaré plots in detecting heart-related diseases or abnormalities.

mini

See also

References

  1. ↑ Yale Fractal Geometry Course Notes
  2. ↑ GLOSSARY OF TERMS USED IN TIME SERIES ANALYSIS OF CARDIOVASCULAR DATA
  3. ↑ Heikki V. Huikuri; Timo H. Mäkikallio; Chung-Kang Peng; Ary L. Goldberger; Ulrik Hintze; Mogens Møller (January 4, 2000). "Fractal Correlation Properties of R-R Interval Dynamics and Mortality in Patients With Depressed Left Ventricular Function After an Acute Myocardial Infarction". Circulation. 101 (1): 47–53. doi:10.1161/01.CIR.101.1.47. ISSN 1524-4539. PMID 10618303. Analysis of time and frequency domain measures of heart rate (HR) variability from 24-hour ambulatory ECG recordings provides prognostic information on patients after an acute myocardial infarction.1–4 A number of new methods based on nonlinear system theory ("chaos theory and fractals") have been recently developed to quantify the complex HR dynamics and to complement the conventional measures of HR variability.5–12 New fractal analysis methods have already provided clinically useful information on patients with impaired left ventricular function,13–15 but their prognostic power has not been proved in large-scale studies. In the present investigation, we assessed the use of various fractal analysis methods of HR variability to predict death in a population of patients with acute myocardial infarction (MI) and depressed left ventricular function. The prediction of death was evaluated in survivors of acute MI included in the Danish Investigations of Arrhythmia and Mortality on Dofetilide (DIAMOND-MI) trial. We also sought to determine whether these new fractal measures of R-R interval dynamics predict specifically either arrhythmic or nonarrhythmic cardiac death.
  4. ↑ Melillo, Paolo; Izzo, Raffaele; Orrico, Ada; Scala, Paolo; Attanasio, Marcella; Mirra, Marco; De Luca, Nicola; Pecchia, Leandro (2015-03-20). "Automatic Prediction of Cardiovascular and Cerebrovascular Events Using Heart Rate Variability Analysis". PLOS ONE. 10 (3): e0118504. Bibcode:2015PLoSO..1018504M. doi:10.1371/journal.pone.0118504. ISSN 1932-6203. PMC 4368686. PMID 25793605.
  5. ↑ "Early detection of sudden cardiac death using Poincaré plots and recurrence plot-based features from HRV signals | Request PDF". ResearchGate. Retrieved 2018-11-12.


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.