The Portevin–Le Chatelier (PLC) effect describes a serrated stress–strain curve or jerky flow, which some materials exhibit as they undergo plastic deformation, specifically inhomogeneous deformation.[1] This effect has been long associated with dynamic strain aging or the competition between diffusing solutes pinning dislocations and dislocations breaking free of this stoppage.[2]

The onset of the PLC effect occurs when the strain rate sensitivity becomes negative and inhomogeneous deformation starts.[1] This effect also can appear on the specimen's surface and in bands of plastic deformation. This process starts at a so-called critical strain, which is the minimum strain needed for the onset of the serrations in the stress–strain curve. The critical strain is both temperature and strain rate dependent.[2] The existence of a critical strain is attributed to better solute diffusivity due to the deformation created vacancies and increased mobile dislocation density. Both of these contribute to the instability in substitutional alloys, while interstitial alloys are only affected by the increase in mobile dislocation densities.[3]

History

While the effect is named after Albert Portevin and François Le Chatelier,[4] they were not the first to discover it. Félix Savart made the discovery when he observed non-homogeneous deformation during a tensile test of copper strips. He documented the physical serrations in his samples that are currently known as Portevin–Le Chatelier bands. A student of Savart, Antoine Masson, repeated the experiment while controlling for loading rate. Masson observed that under a constant loading rate, the samples would experience sudden large changes in elongation (as large as a few millimeters).[5]

Underlying physics

Much of the underlying physics of the Portevin-Le Chatelier effect lies in a specific case of solute drag creep. Adding solute atoms to a pure crystal introduces a size misfit into the system. This size misfit leads to restriction of dislocation motion.  At low temperature, these solute atoms are immobile within the lattice, but at high temperatures, the solute atoms become mobile and interact in a more complex manner with the dislocations. When solute atoms are mobile and the dislocation velocity is not too high, the solute atoms and dislocation can move together where the solute atom decreases the motion of the dislocation.[6]

The Portevin-Le Chatelier effect occurs in the specific case where solute drag creep is occurring and there is an applied stress, with a material dependent range, on the sample. The applied stress causes the velocity of the dislocations to increase, allowing the dislocation to move away from the solute. This process is commonly referred to as “breakaway”. Once the dislocation has moved away from the solute, the stress on it decreases which causes its velocity to decrease. This allows the solute atoms to “catch up” with the dislocation. As soon as the solute atom catches up, the stress on the dislocation significantly increases, causing the process to repeat.[6]  

The cyclic changes described above produce serrations in the plastic region of the stress strain diagram of a tensile test that is undergoing the Portevin-Le Chatelier effect. The variation in stress also causes non-homogeneous deformation to occur throughout the sample which can be visible to the naked eye through observation of a rough finish.[5]

Conditions that affect the PLC effect

Temperature

Temperature affects both the speed of band propagation through the material and the critical strain. The speed of band propagation is proportional to the temperature (lower temp lower speeds, higher temp higher speeds). Often the critical strain will first decrease due to temperature.[2] The temperature effect on the PLC regime is caused by the increased ability of the solutes to diffuse to the dislocations with increasing temperature. Although the mechanism of diffusion is not entirely understood, it is believed that solute atoms diffuse by either volume (high temperature), by diffusion in stacking fault ribbons between partial dislocations (intermediate temperature) or pipe diffusion (low temperature).[3]

Strain rate

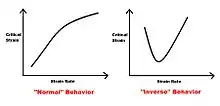
While temperature is related to the rate of diffusion, strain rate determines the time the dislocations take to overcome these obstacles, and has a dramatic effect on the conditions of the PLC effect. So generally, the critical stress will decrease with imposed strain rate.[3] Also the higher the stress rate, the lower the band speed.[2]

Precipitates

Precipitates, often found in Al alloys (especially of the Mg variety), complicate the PLC effect.

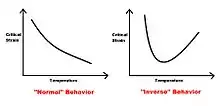
Critical strain vs temperature normal vs. inverse behavior

Often these precipitates will cause the so-called inverse behavior, which changes the effect of both strain rate and temperature on the solid[7] The presence of precipitates is shown to have an influence on the appearance and disappearance of serrations in the stress strain curve.

Strain rate vs critical strain normal vs. inverse behavior

[8]

Grain size

The structure of the material, as well, has an effect on the appearance and parameters that describe the PLC effect. For example, the magnitude of the stress drops is larger with a smaller grain size. The critical strain often increases with larger grains, which is linked to the dependence of the dislocation density to grain size.[8] Serration amplitude is greater in Al-Mg alloys for a finer grain size. There is a correlation between increasing the critical strain and the onset of serration with increasing grain size.[9] But some findings indicate that the grain size has practically no effect on the band velocity or the band width.[3]

Material finish

Polishing the material affects the beginning of the PLC effect and the band velocities. Apparently a rougher surface provides more nucleation points for high stress, which help initiate deformation bands. These bands also propagate twice as fast in the polished specimen.[2]

Non effects

The number of vacancies does not directly affect the PLC start point. It was found that if a material is pre-strained to a value ½ of that required to initiate jerky flow, and then rested at the test temperature or annealed to remove vacancies (but low enough that the dislocation structure is not affected), then the total critical strain is only slightly decreased as well as the types of serrations that do occur.[10]

Serrations descriptors

While properties like strain rate sensitivity and critical strain mark the beginning of the PLC effect, people have developed a system to describe the serrations themselves. These types are often dependent on strain rate, temperature, and grain size.[8] While usually the bands are labeled A, B, and C some sources have added a D and E type Bands.[11] Because the type A, B, and C type bands are most found in literature they will be the only ones covered here.

Serration types

Type A bands

Type A bands are often seen at high strain rate and low temperatures.[11] They are a random development of bands that form over the entire specimen.[12] They are usually described as continuously propagating with small stress drops.[3]

Type B bands

Type B bands are sometimes described as “hopping” bands and they appear at a medium to high strain rates.[12] They are often seen as each band forming ahead of the previous one in a spatially correlated way. The serrations are more irregular with smaller amplitudes than type C.[3]

Type C bands

C bands are often seen at low applied strain rate or high temperatures.[11] These are identified with random nucleated static bands with large characteristic stress drops the serration.[3]

Other notes on band types

The different types of bands are believed to represent different states of dislocation in the bands, and band types can change in a materials stress strain curve. Currently there are no models that can capture the change in band types [3]

Portevin-Le Chatelier (PLC) effect is a proof of non-uniform deformation of CuNi25 commercial alloys at intermediate temperature. In CuNi25 alloy it manifests itself as irregularities in the form of serrations on the stress–strain curve. It proves instability of force during tension and heterogeneity of microstructure and presence of many heterogeneous factors, affecting its mechanical properties.[13]

Problems caused by the PLC effect

Because the PLC effect is related to a strengthening mechanism, the strength of steel may increase; however, the plasticity and ductility of a material afflicted by the PLC effect decrease drastically. The PLC effect is known to induce blue brittleness in steel; additionally, the loss of ductility may cause rough surfaces to develop during deformation (Al-Mg alloys are especially susceptible to this), rendering them useless for autobody or casting applications.[2]

References

  1. 1 2 Van Den Beukel, A. (1975). "Theory of the effect of dynamic strain aging on mechanical properties". Physica Status Solidi A. 30 (1): 197–206. Bibcode:1975PSSAR..30..197V. doi:10.1002/pssa.2210300120.
  2. 1 2 3 4 5 6 Abbadi, M.; Hähner, P.; Zeghloul, A. (2002). "On the characteristics of Portevin–Le Chatelier bands in aluminum alloy 5182 under stress-controlled and strain-controlled tensile testing". Materials Science and Engineering: A. 337 (1–2): 194–201. doi:10.1016/S0921-5093(02)00036-9.
  3. 1 2 3 4 5 6 7 8 Ananthakrishna, G. (2007). "Current theoretical approaches to collective behavior of dislocations". Physics Reports. 440 (4–6): 113–259. Bibcode:2007PhR...440..113A. doi:10.1016/j.physrep.2006.10.003.
  4. ↑ Portevin, Albert; Le Chatelier, François (1923). "Sur un phénomène observé lors de l'essai de traction d'alliages en cours de transformation" [On a phenomenon observed in the tensile testing of alloys during processing]. Comptes rendus hebdomadaires des séances de l'Académie des sciences (in French). 176: 507–510.
  5. 1 2 Franklin, Scott V.; Mertens, F.; Marder, M. (1 December 2000). "Portevin–Le Chatelier effect". Physical Review E. 62 (6): 8195–8206. Bibcode:2000PhRvE..62.8195F. doi:10.1103/PhysRevE.62.8195. PMID 11138118.
  6. 1 2 Courtney, Thomas H. (2000). Mechanical behavior of materials (2nd ed.). Boston: McGraw Hill. ISBN 0070285942. OCLC 41932585.
  7. ↑ Brechet, Y.; Estrin, Y. (1995). "On the influence of precipitation on the Portevin-Le Chatelier effect". Acta Metallurgica et Materialia. 43 (3): 955–963. doi:10.1016/0956-7151(94)00334-E.
  8. 1 2 3 Mannan, S. L. (1993). "Role of dynamic strain ageing in low cycle fatigue". Bulletin of Materials Science. 16 (6): 561–582. doi:10.1007/BF02757656. S2CID 137504868.
  9. ↑ Van Den Beukel, A.; Kocks, U.F. (1982). "The strain dependence of static and dynamic strain-aging". Acta Metallurgica. 30 (5): 1027–1034. doi:10.1016/0001-6160(82)90211-5.
  10. ↑ Mulford, R.A.; Kocks, U.F. (1979). "New observations on the mechanisms of dynamic strain aging and of jerky flow". Acta Metallurgica. 27 (7): 1125–1134. doi:10.1016/0001-6160(79)90130-5.
  11. 1 2 3 Rodriguez, P. (1984). "Serrated plastic flow". Bulletin of Materials Science. 6 (4): 653–663. doi:10.1007/BF02743993. S2CID 136872405.
  12. 1 2 Bruggemann, C., Bohlke, T, Bertram, A. (2008) "Modeling and simulation of the Portevin Le Chatelier Effect" Micro-Macro-Interactions: In Structured Media and Particle SystemsBerlin: Springer-Verlag:53–62
  13. ↑ Sakiewicz, P.; Nowosielski, R.; Babilas, R. (August 2015). "Production aspects of inhomogeneous hot deformation in as-cast CuNi25 alloy" (PDF). Indian Journal of Engineering & Materials Sciences. 22: 389–398.

See also

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.