Pseudo-deltoidal icositetrahedron

(see 3D model)
TypeJohnson dual,
pseudo-uniform dual
Faces24, congruent
Face polygon
Kite with:
1 obtuse angle
3 equal acute angles
Edges24 short + 24 long = 48
Vertices8 of degree 3
18 of degree 4
26 in all
Vertex configurations4.4.4 (for 8 vertices)
4.4.4.4 (for 2+8+8 vertices)
Symmetry groupD4d = D4v, [2+,24], (2*4), order 4×4
Rotation groupD4, [2,4]+, (224), order 2×4
Dihedral anglesame value for short & long edges:

Propertiesconvex, regular vertices[1]
Net
(click to enlarge)
Dual polyhedron

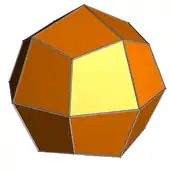
The pseudo-deltoidal icositetrahedron is a convex polyhedron with 24 congruent kites as its faces. It is the dual of the elongated square gyrobicupola, also known as the pseudorhombicuboctahedron.

As the pseudorhombicuboctahedron is tightly related to the rhombicuboctahedron, but has a twist along an equatorial belt of faces (and edges), the pseudo-deltoidal icositetrahedron is tightly related to the deltoidal icositetrahedron, but has a twist along an equator of (vertices and) edges.

Properties

Vertices

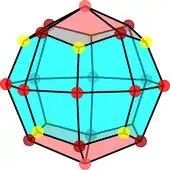
As the faces of the pseudorhombicuboctahedron are regular, the vertices of the pseudo-deltoidal icositetrahedron are regular.[1] But due to the twist, these 26 vertices are of four different kinds:

  • eight vertices connecting three short edges (yellow vertices in 1st figure below),
  • two apices connecting four long edges (top and bottom vertices, light red in 1st figure below),
  • eight vertices connecting four alternate edges: short-long-short-long (dark red vertices in 1st figure below),
  • eight vertices connecting one short and three long edges (twisted-equator vertices, medium red in 1st figure below).

Edges

A pseudo-deltoidal icositetrahedron has 48 edges: 24 short and 24 long, in the ratio of — their lengths are and respectively, if its dual pseudo-rhombicuboctahedron has unit edge length.[2]

Faces

As the pseudorhombicuboctahedron has only one type of vertex figure, the pseudo-deltoidal icositetrahedron has only one shape of face (it is monohedral); its faces are congruent kites. But due to the twist, the pseudorhombicuboctahedron is not vertex-transitive, with its vertices in two different symmetry orbits (*), and the pseudo-deltoidal icositetrahedron is not face-transitive, with its faces in two different symmetry orbits (*) (it is 2-isohedral); these 24 faces are of two different kinds:

  • eight faces with light red, dark red, yellow, dark red vertices (top and bottom faces, light red in 1st figure below),
  • sixteen faces with yellow, dark red, medium red, medium red vertices (side faces, blue in 1st figure below).

(*) (three different symmetry orbits if we only consider rotational symmetries)

Pseudo- and actual deltoidal icositetrahedron
Pseudo- and actual rhombicuboctahedron
Pseudo- and actual deltoidal icositetrahedron
Pseudo- and actual great deltoidal icositetrahedron
Pseudo-deltoidal icositetrahedron as die

References

  1. 1 2 "duality". www.polyhedra-world.nc. Retrieved 2022-10-26.
  2. ↑ http://mathworld.wolfram.com/DeltoidalIcositetrahedron.html
Wikimedia Commons has media related to Pseudo-strombic icositetrahedron.


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.