A pulse in signal processing is a rapid, transient change in the amplitude of a signal from a baseline value to a higher or lower value, followed by a rapid return to the baseline value.[1]
Pulse shapes
Pulse shapes can arise out of a process called pulse-shaping. Optimum pulse shape depends on the application.
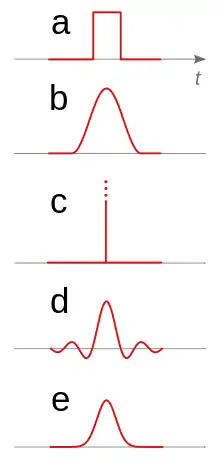
Rectangular pulse
These can be found in pulse waves, square waves, boxcar functions, and rectangular functions. In digital signals the up and down transitions between high and low levels are called the rising edge and the falling edge. In digital systems the detection of these sides or action taken in response is termed edge-triggered, rising or falling depending on which side of rectangular pulse. A digital timing diagram is an example of a well-ordered collection of rectangular pulses.
Nyquist pulse
A Nyquist pulse is one which meets the Nyquist ISI criterion and is important in data transmission. An example of a pulse which meets this condition is the sinc function. The sinc pulse is of some significance in signal-processing theory but cannot be produced by a real generator for reasons of causality.
In 2013, Nyquist pulses were produced in an effort to reduce the size of pulses in optical fibers, which enables them to be packed 10 times more closely together, yielding a corresponding 10-fold increase in bandwidth. The pulses were more than 99 percent perfect and were produced using a simple laser and modulator.[2][3]
Dirac pulse
A Dirac pulse has the shape of the Dirac delta function. It has the properties of infinite amplitude and its integral is the Heaviside step function. Equivalently, it has zero width and an area under the curve of unity. This is another pulse that cannot be created exactly in real systems, but practical approximations can be achieved. It is used in testing, or theoretically predicting, the impulse response of devices and systems, particularly filters. Such responses yield a great deal of information about the system.
Gaussian pulse
A Gaussian pulse is shaped as a Gaussian function and is produced by the impulse response of a Gaussian filter. It has the properties of maximum steepness of transition with no overshoot and minimum group delay.
See also
References
- ↑ Ángela Molina, Joaquín González, Pulse Voltammetry in Physical Electrochemistry and Electroanalysis, Springer, 2015 ISBN 3319212516.
- ↑ Joel Detrow. "Pointy pulses improve optical fiber throughput by a factor of 10". Gizmag.com. Retrieved 2013-12-06.
- ↑ Marcelo A. Soto; Mehdi Alem; Mohammad Amin Shoaie; Armand Vedadi; Camille-Sophie Brès; Luc Thévenaz; Thomas Schneider. "Optical sinc-shaped Nyquist pulses of exceptional quality : Nature Communications : Nature Publishing Group". Nature.com. Retrieved 2013-12-07.
{{cite journal}}: Cite journal requires|journal=(help)