Pointer jumping or path doubling is a design technique for parallel algorithms that operate on pointer structures, such as linked lists and directed graphs. Pointer jumping allows an algorithm to follow paths with a time complexity that is logarithmic with respect to the length of the longest path. It does this by "jumping" to the end of the path computed by neighbors.

The basic operation of pointer jumping is to replace each neighbor in a pointer structure with its neighbor's neighbor. In each step of the algorithm, this replacement is done for all nodes in the data structure, which can be done independently in parallel. In the next step when a neighbor's neighbor is followed, the neighbor's path already followed in the previous step is added to the node's followed path in a single step. Thus, each step effectively doubles the distance traversed by the explored paths.

Pointer jumping is best understood by looking at simple examples such as list ranking and root finding.

List ranking

One of the simpler tasks that can be solved by a pointer jumping algorithm is the list ranking problem. This problem is defined as follows: given a linked list of N nodes, find the distance (measured in the number of nodes) of each node to the end of the list. The distance d(n) is defined as follows, for nodes n that point to their successor by a pointer called next:

• If n.next is nil, then d(n) = 0.
• For any other node, d(n) = d(n.next) + 1.

This problem can easily be solved in linear time on a sequential machine, but a parallel algorithm can do better: given n processors, the problem can be solved in logarithmic time, O(log N), by the following pointer jumping algorithm:^[1]: 693

The pointer jumping occurs in the last line of the algorithm, where each node's next pointer is reset to skip the node's direct successor. It is assumed, as in common in the PRAM model of computation, that memory access are performed in lock-step, so that each n.next.next memory fetch is performed before each n.next memory store; otherwise, processors may clobber each other's data, producing inconsistencies.^[1]: 694

The following diagram follows how the parallel list ranking algorithm uses pointer jumping for a linked list with 11 elements. As the algorithm describes, the first iteration starts initialized with all ranks set to 1 except those with a null pointer for next. The first iteration looks at immediate neighbors. Each subsequent iteration jumps twice as far as the previous.

Analyzing the algorithm yields a logarithmic running time. The initialization loop takes constant time, because each of the N processors performs a constant amount of work, all in parallel. The inner loop of the main loop also takes constant time, as does (by assumption) the termination check for the loop, so the running time is determined by how often this inner loop is executed. Since the pointer jumping in each iteration splits the list into two parts, one consisting of the "odd" elements and one of the "even" elements, the length of the list pointed to by each processor's n is halved in each iteration, which can be done at most O(log N) time before each list has a length of at most one.^{[1]: 694–695}

Root finding

Following a path in a graph is an inherently serial operation, but pointer jumping reduces the total amount of work by following all paths simultaneously and sharing results among dependent operations. Pointer jumping iterates and finds a successor — a vertex closer to the tree root — each time. By following successors computed for other vertices, the traversal down each path can be doubled every iteration, which means that the tree roots can be found in logarithmic time.

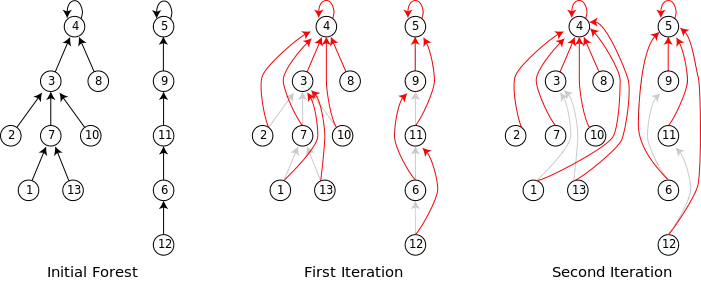
Pointer doubling operates on an array successor with an entry for every vertex in the graph. Each successor[i] is initialized with the parent index of vertex i if that vertex is not a root or to i itself if that vertex is a root. At each iteration, each successor is updated to its successor's successor. The root is found when the successor's successor points to itself.

The following pseudocode demonstrates the algorithm.

algorithm
    Input: An array parent representing a forest of trees. parent[i] is the parent of vertex i or itself for a root
    Output: An array containing the root ancestor for every vertex

    for i ← 1 to length(parent) do in parallel
        successor[i] ← parent[i]
    while true
        for i ← 1 to length(successor) do in parallel
            successor_next[i] ← successor[successor[i]]
        if successor_next = successor then
            break
        for i ← 1 to length(successor) do in parallel
            successor[i] ← successor_next[i]
    return successor

The following image provides an example of using pointer jumping on a small forest. On each iteration the successor points to the vertex following one more successor. After two iterations, every vertex points to its root node.

History and examples

Although the name pointer jumping would come later, JáJá^[2]: 88 attributes the first uses of the technique in early parallel graph algorithms^[3][4]: 43 and list ranking.^[5] The technique has been described with other names such as shortcutting,^[6][7] but by the 1990s textbooks on parallel algorithms consistently used the term pointer jumping.^{[2]: 52–56 [1]: 692–701 [8]: 34–35} Today, pointer jumping is considered a software design pattern for operating on recursive data types in parallel.^[9]: 99

As a technique for following linked paths, graph algorithms are a natural fit for pointer jumping. Consequently, several parallel graph algorithms utilizing pointer jumping have been designed. These include algorithms for finding the roots of a forest of rooted trees,^{[2]: 52–53 [6]} connected components,^{[2]: 213–221} minimum spanning trees^[2],^{: 222–227 [10]} and biconnected components^{[2]: 227–239 [7]}. However, pointer jumping has also shown to be useful in a variety of other problems including computer vision,^[11] image compression,^[12] and Bayesian inference.^[13]

References