Surface roughness scattering or interface roughness scattering is the elastic scattering of particles against a rough solid surface or imperfect interface between two different materials. This effect has been observed in classical systems, such as microparticle scattering,^[1] as well as quantum systems, where it arises electronic devices, such as field effect transistors and quantum cascade lasers.^[2]

Classical description

In the classical mechanics framework, a rough surface, such as a machined metal surface, randomizes the probability distribution function governing the incoming particles, leading to net momentum loss of the particle flux.^[3]

Quantum description

The energy of charged particles in a quantum well is strongly affected by its thickness.

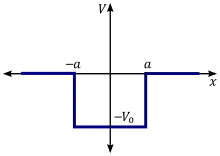
In the quantum mechanical framework, this scattering is most noticeable in confined systems, in which the energies for charge carriers are determined by the locations of interfaces. An example of such a system is a quantum well, which may be constructed from a sandwich of different layers of semiconductor. Variations in the thickness of these layers therefore causes the energy of particles to be dependent on their in-plane location in the layer.^[4] Classification of the roughness at a given position, ${\displaystyle \Delta _{z}(\mathbf {r} )}$, is complex, but as in the classical models, it has been modeled as a Gaussian distribution by some researchers ^[5] This assumption may be formulated in terms of the ensemble average for some given characteristic height, ${\displaystyle \Delta }$, and correlation length, ${\displaystyle \Lambda }$, such that

${\displaystyle \langle \Delta _{z}(\mathbf {r} )\Delta _{z}(\mathbf {r'} )\rangle =\Delta ^{2}\exp \left(-{\frac {|\mathbf {r} -\mathbf {r'} |^{2}}{\Lambda ^{2}}}\right)}$

Types of Scattering

Selective Scattering : In selective Scattering scattering depends upon the wavelength of light.

Mie scattering : Mie theory can describe how electromagnetic waves interact with homogeneously spherical particles. However, a theory for homogeneous spheres will completely fail to predict polarization effects.^[6][7] When the size of the molecules is greater than the wavelength of light, the result is a non-uniform scattering of light.

Lambertian Scattering: This type of scattering occurs when a surface has microscopic irregularities that scatter light perfectly uniformly in all directions, causing it to appear equally bright from all viewing angles.

Subsurface Scattering: This type of scattering occurs when light scatters within a material before exiting the surface at a different point.

Isotropic crystal scattering (aka powder diffraction): This type of scattering occurs when every crystalline orientation is represented equally in a powdered sample. Powder X-ray diffraction (PXRD) operates under the assumption that the sample is randomly arranged such that each plane will be represented in the signal.

Notes