In control engineering, the sensitivity (or more precisely, the sensitivity function) of a control system measures how variations in the plant parameters affects the closed-loop transfer function. Since the controller parameters are typically matched to the process characteristics and the process may change, it is important that the controller parameters are chosen in such a way that the closed loop system is not sensitive to variations in process dynamics. Moreover, the sensitivity function is also important to analyse how disturbances affects the system.
Sensitivity function
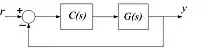
Let and denote the plant and controller's transfer function in a basic closed loop control system written in the Laplace domain using unity negative feedback.
Sensitivity function as a measure of robustness to parameter variation
The closed-loop transfer function is given by
Differentiating with respect to yields
where is defined as the function
and is known as the sensitivity function. Lower values of implies that relative errors in the plant parameters has less effects in the relative error of the closed-loop transfer function.
Sensitivity function as a measure of disturbance attenuation
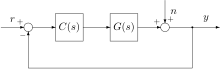
The sensitivity function also describes the transfer function from external disturbance to process output. In fact, assuming an additive disturbance n after the output
of the plant, the transfer functions of the closed loop system are given by
Hence, lower values of suggest further attenuation of the external disturbance. The sensitivity function tells us how the disturbances are influenced by feedback. Disturbances with frequencies such that is less than one are reduced by an amount equal to the distance to the critical point and disturbances with frequencies such that is larger than one are amplified by the feedback.[1]
Sensitivity peak and sensitivity circle
Sensitivity peak
It is important that the largest value of the sensitivity function be limited for a control system. The nominal sensitivity peak is defined as[2]
and it is common to require that the maximum value of the sensitivity function, , be in a range of 1.3 to 2.
Sensitivity circle
The quantity is the inverse of the shortest distance from the Nyquist curve of the loop transfer function to the critical point . A sensitivity guarantees that the distance from the critical point to the Nyquist curve is always greater than and the Nyquist curve of the loop transfer function is always outside a circle around the critical point with the radius , known as the sensitivity circle. defines the maximum value of the sensitivity function and the inverse of gives you the shortest distance from the open-loop transfer function to the critical point .[3][4]
References
- ↑ K.J. Astrom, "Model uncertainty and robust control," in Lecture Notes on Iterative Identification and Control Design. Lund, Sweden: Lund Institute of Technology, Jan. 2000, pp. 63–100.
- ↑ K.J. Astrom and T. Hagglund, PID Controllers: Theory, Design and Tuning, 2nd ed. Research Triangle Park, NC 27709, USA: ISA - The Instrumentation, Systems, and Automation Society, 1995.
- ↑ A. G. Yepes, et al., "Analysis and design of resonant current controllers for voltage-source converters by means of Nyquist diagrams and sensitivity function" in IEEE Trans. on Industrial Electronics, vol. 58, No. 11, Nov. 2011, pp. 5231–5250.
- ↑ Karl Johan Åström and Richard M. Murray. Feedback systems : an introduction for scientists and engineers. Princeton University Press, Princeton, NJ, 2008.