In mathematics, the sinhc function appears frequently in papers about optical scattering,[1] and hyperbolic geometry.[2] For , it is defined as[3][4]
_plotted_in_the_complex_plane_from_-2-2i_to_2%252B2i.svg.png.webp)
The cardinal hyperbolic sine function sinhc(z) plotted in the complex plane from -2-2i to 2+2i
The sinhc function is the hyperbolic analogue of the sinc function, defined by . It is a solution of the following differential equation:
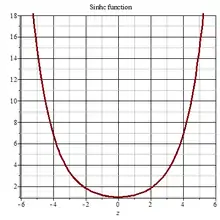
Sinhc 2D plot
_2D_plot.png.webp)
Sinhc'(z) 2D plot
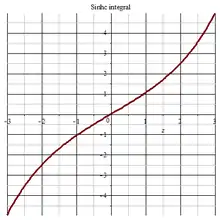
Sinhc integral 2D plot
Properties
The first-order derivative is given by
The Taylor series expansion is
The Padé approximant is
In terms of other special functions
- , where is Kummer's confluent hypergeometric function.
- , where is the biconfluent Heun function.
- , where is a Whittaker function.
Gallery
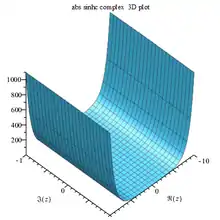 Sinhc abs complex 3D |
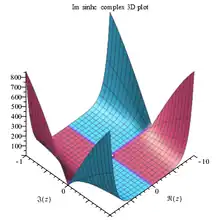 Sinhc Im complex 3D plot |
 Sinhc Re complex 3D plot |
_Im_complex_3D_plot.png.webp) Sinhc'(z) Im complex 3D plot |
_Re_complex_3D_plot.png.webp) Sinhc'(z) Re complex 3D plot |
_abs_complex_3D_plot.png.webp) Sinhc'(z) abs complex 3D plot |
 Sinhc abs plot |
 Sinhc Im plot |
 Sinhc Re plot |
_Im_plot.JPG.webp) Sinhc'(z) Im plot |
_abs_plot.JPG.webp) Sinhc'(z) abs plot |
_Re_plot.JPG.webp) Sinhc'(z) Re plot |
See also
References
- ↑ den Outer, P. N.; Lagendijk, Ad; Nieuwenhuizen, Th. M. (1993-06-01). "Location of objects in multiple-scattering media". Journal of the Optical Society of America A. 10 (6): 1209. Bibcode:1993JOSAA..10.1209D. doi:10.1364/JOSAA.10.001209. ISSN 1084-7529.
- ↑ Nilgün Sönmez, A Trigonometric Proof of the Euler Theorem in Hyperbolic Geometry, International Mathematical Forum, 4, 2009, no. 38, 1877–1881
- ↑ ten Thije Boonkkamp, J. H. M.; van Dijk, J.; Liu, L.; Peerenboom, K. S. C. (2012). "Extension of the Complete Flux Scheme to Systems of Conservation Laws". Journal of Scientific Computing. 53 (3): 552–568. doi:10.1007/s10915-012-9588-5. ISSN 0885-7474. S2CID 8455136.
- ↑ Weisstein, Eric W. "Sinhc Function". mathworld.wolfram.com. Retrieved 2022-11-17.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.