Moderately difficult Slitherlink puzzle (solution)

Slitherlink (also known as Fences, Takegaki, Loop the Loop, Loopy, Ouroboros, Suriza, Rundweg and Dotty Dilemma) is a logic puzzle developed by publisher Nikoli.

Rules

Slitherlink is played on a rectangular lattice of dots. Some of the squares formed by the dots have numbers inside them. The objective is to connect horizontally and vertically adjacent dots so that the lines form a simple loop with no loose ends. In addition, the number inside a square represents how many of its four sides are segments in the loop.

Other types of planar graphs can be used in lieu of the standard grid, with varying numbers of edges per vertex or vertices per polygon. These patterns include snowflake, Penrose, Laves and Altair tilings. These add complexity by varying the number of possible paths from an intersection, and/or the number of sides to each polygon; but similar rules apply to their solution.

Solution methods

Notation

Whenever the number of lines around a cell matches the number in the cell, the other potential lines must be eliminated. This is usually indicated by marking an X on lines known to be empty.

Another useful notation when solving Slitherlink is a ninety degree arc between two adjacent lines, to indicate that exactly one of the two must be filled. A related notation is a double arc between adjacent lines, indicating that both or neither of the two must be filled. These notations are not necessary to the solution, but can be helpful in deriving it.

Arc notation around a 2 in a corner.

Many of the methods below can be broken down into two simpler steps by use of arc notation.

Exactly 2 or 0 lines at each point

A key to many deductions in Slitherlink is that every point has either exactly two lines connected to it, or no lines. So if a point which is in the centre of the grid, not at an edge or corner, has three incoming lines which are X'd out, the fourth must also be X'd out. This is because the point cannot have just one line - it has no exit route from that point. Similarly, if a point on the edge of the grid, not at a corner, has two incoming lines which are X'd out, the third must also be X'd out. And if a corner of the grid has one incoming line which is X'd out, the other must also be X'd out.

Application of this simple rule leads to increasingly complex deductions. Recognition of these simple patterns will help greatly in solving Slitherlink puzzles.

Corners

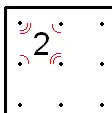
  • If a 1 is in a corner, the actual corner's lines may be X'd out, because a line that entered said corner could not leave it except by passing by the 1 again. This also applies if two lines leading into the 1-box at the same corner are X'd out.
A 1 in a corner.
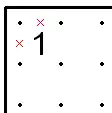
  • If a 3 is in a corner, the two outside edges of that box can be filled in because otherwise the rule above would have to be broken.
A 3 in a corner.
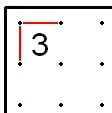
  • If a 2 is in a corner, two lines must be going away from the 2 at the border.
A 2 in a corner.

Rules for squares with 1

  • If a line comes into a corner of a 1 and if one of the three remaining directions that the line can continue, the one that is not a side of the 1 is a known blank, then the two sides of the 1 opposite that corner can be X'd out.
A 1 next to a line.
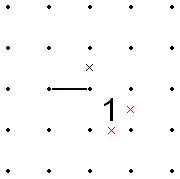
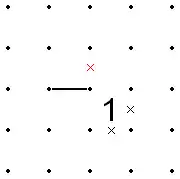
  • This also applies in reverse. That is, if a line comes into the corner of a 1, and the two opposite edges of the 1 are already X'd out, the line cannot go away from the 1 since that would put Xs around all sides of the 1.
A 1 next to a line (opposite)
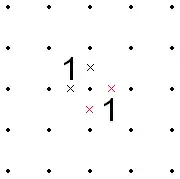
  • If two 1s are diagonally adjacent, then of the eight segments around those two cells, either the "inner" set of four segments sharing a common endpoint (the point shared by the 1s) or the other "outer" set of four segments must all be X'd out. Thus if any two inner or outer segments in one 1 are X'd, the respective inner or outer segments of the other 1 must also be X'd.
Diagonally adjacent 1s
Diagonally adjacent 1s
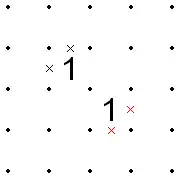
  • If two 1s are adjacent along the edge of the grid, the line between them can be X'd out, because there would be no direction for it to continue when it reached the edge.

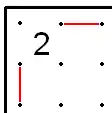
A rule for squares with 2

If a 2 has any surrounding line X’d, then a line coming into either of the two corners not adjacent to the X’d out line cannot immediately exit at right angles away from the 2, as then two lines around the 2 would be impossible, and can therefore be X’d. This means that the incoming line must continue on one side of the 2 or the other. This in turn means that the second line of the 2 must be on the only remaining free side, adjacent to the originally X’d line, so that can be filled in.
Conversely, if a 2 has a line on one side, and an adjacent X’d out line, then the second line must be in one of the two remaining sides, and exit from the opposite corner (in either direction). If either of those two exits is X’d out, then it must take the other route.

A 2 next to a line.

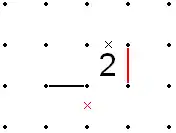
Rules for squares with 3

  • If a 3 is adjacent to a 0, either horizontally or vertically, then all edges of that 3 can be filled except for the one touching the 0. In addition, the two lines perpendicular to the adjacent boxes can be filled.
A 3 adjacent to an 0.
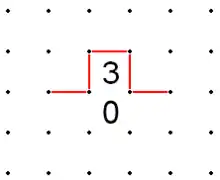
  • If two 3s are adjacent to each other horizontally or vertically, their common edge must be filled in, because the only other option is a closed oval that is impossible to connect to any other line. Second, the two outer lines of the group (parallel to the common line) must be filled in. Thirdly, the line through the 3s will always wrap around in an "S" shape. Therefore, the line between the 3s cannot continue in a straight line, and those sides which are in a straight line from the middle line can be X'd out.
Two adjacent 3s.
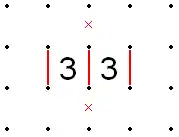
  • If a 3 is adjacent to a 0 diagonally, both sides of the 3 that meet the 0's corner must be filled. This is because if either of those sides were open, the line ending in the corner of the 0 would have no place to go. This is similar to the 3-in-a-corner rule.
3 diagonally next to 0.
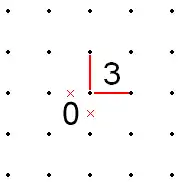
  • Similarly, if a 3 has a corner with Xs in both directions going away from that corner, then both sides of the 3 that meet that corner must be filled. This is because if one of those two sides of the 3 were open, the other would have to be filled (because the 3 can only have one open side) but would meet 3 Xs at that corner, which is impossible because each point on the grid must have exactly 2 or 0 lines.
  • If a line reaches a corner of a 3, there must be lines on both sides of the 3 that said corner is not adjacent to, because if the 3's sole empty space were not adjacent to it, the corner would have three lines connected to it. Furthermore, the segment leading away from the 3 at the corner reached by the line must be empty; if it were filled, neither of the remaining 2 undetermined sides of the 3 would be able to contain a line.
A 3 next to a line.

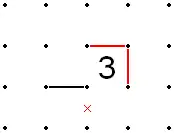
Diagonals of 3s and 2s

  • If two 3s are adjacent diagonally, the edges which do not run into the common point must be filled in.
Two diagonal 3s.
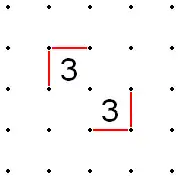
  • Similarly, if two 3s are in the same diagonal, but separated by any number of 2s (and only 2s) the outside edges of the 3s must be filled in, just as if they were adjacent diagonally.
Diagonal 3s with 2 between them.
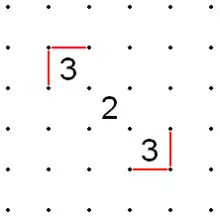
  • If there is a series of 2s in a diagonal line and an angled line meets the corner of the 2 at one end of the series, a matching angled line can be drawn all the way up the series.
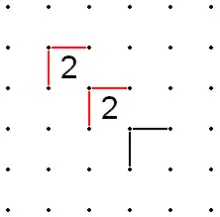
One or more diagonal 2s terminated by two filled lines pointing into them.
  • If a line reaches the starting point (A) of a diagonal that contains one or more 2s and ends with a 3, both sides of the far corner (farthest from A on the diagonal) of the 3 must be filled. If this were not true, it would imply that both sides of the near corner of the 3 must be filled, which would imply that the near corners of all the 2s must be filled, including the 2 at the start of the diagonal, which is impossible because it conflicts with the line that has reached the starting point (A).
A diagonal of 2s ending with a 3.

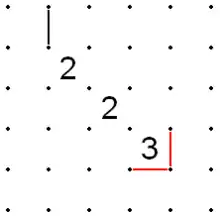
Diagonals of a 3 and 1

  • If a 1 and a 3 are adjacent diagonally and the outer two sides of the 1 are X'd out, then the outer two sides of the 3 must be filled in.
Diagonals of a 3 and 1
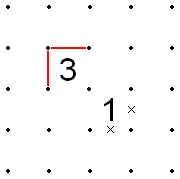
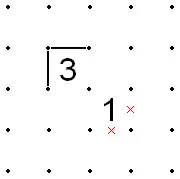
  • The opposite is the same: if the outer two corners of the 3 are filled in, then the outer two corners of the 1 must be X'd out.
Diagonals of a 3 and 1 opposite

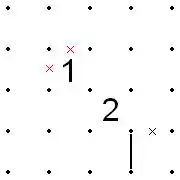
Diagonals starting with a 2

  • If a line reaches a corner of a 2, and the line must continue through one of the two connecting sides of the 2, then exactly one of the other two sides of the 2 must be filled, and that line must continue through one of the two connecting sides of the diagonally adjacent square.

A rule for closed regions

If a region of the lattice is closed-off (such that no lines can "escape"), and is not empty, there must be a non-zero, even number of lines entering the region that begin outside the region. (An odd number of lines entering implies an odd number of segment ends inside the region, which makes it impossible for all the segment ends to connect. If there are no such lines, the lines inside the region cannot connect with the lines outside, making a solution impossible.) Often, this rule will eliminate one or more otherwise feasible options.

In the figure below, the line at the top-left will close off the top-right region of the lattice whether it proceeds down or to the right. The line to the right (around two sides of the 3) has entered the closed region. To satisfy the rule, the first line must enter the region, and the second line must not enter the region a second time. (Since the boundary of any closed region also closes off the remainder of the puzzle, the rule can also be applied to the larger, bottom-left region. To apply the rule, it is only necessary to count the lines crossing the boundary.)

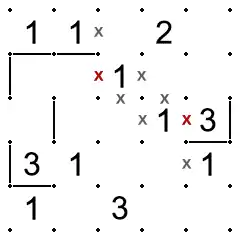
Jordan curve theorem

In an exceptionally difficult puzzle, one may use the Jordan curve theorem, which states that any open curve that starts and ends outside of a closed curve must intersect the closed curve an even number of times. In particular, this means that any row of the grid must have an even number of vertical lines and any column must have an even number of horizontal lines. When only one potential line segment in one of these groups is unknown, you can determine whether it is part of the loop or not with this theorem. This also means that if you mentally trace an arbitrary path from an outer edge of the grid, to another outer edge of the grid, the path will intersect the closed curve an even number of times.

A simple strategy to assist in using this theorem is to "paint" (sometimes called "shade") the outside and the inside areas. When you see two outside cells, or two inside cells next to each other, then you know that there is not a line between them. The converse is also true: if you know there is no line between two cells, then those cells must be the same "color" (both inside or both outside). Similarly, if an outside cell and an inside cell are adjacent, you know there must be a filled line between them; and again the converse is true.

Rules for puzzles that have only 1 solution

  • If there are exactly two possible paths, A and B, between two points in the solution (two points that have been, or must be, reached by lines); and if a solution containing A must also work with B, and the reverse is not true; then B is the correct path, and the solution must pass through a point contained in A but not B.

In the figure below, if a solution could pass through the top and right sides of the 2, then there must be another solution which is exactly the same except that it passes through the bottom and left sides of the 2, because the squares to the top and right of the 2 are unconstrained (do not contain numbers). Also, the solution must pass through the top-right corner of the 2, otherwise there must be another solution which is exactly the same except that it passes through the top and right sides of the 2.

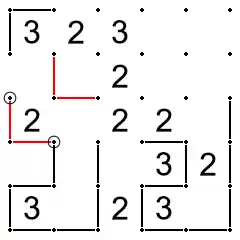
If there is a 2 in a corner, and the two non-diagonally adjacent squares are unconstrained, lines can be drawn as shown below. (In the figure, the question mark represents any number or blank, but the number will only be a 2 or 3. A puzzle with only one solution cannot have a 2 in a corner with two non-diagonally adjacent, unconstrained squares, and a diagonally adjacent 0 or 1.)

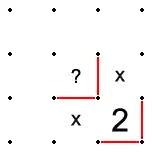
  • If there are two paths between two points, such that a solution containing one must also work with the other, then both paths can be ruled out.

In the figure below, the circled points can be connected by a line directly between them, and also by a line that traverses the other three sides of the square that extends to the left of the points. It should be clear (with the red line ignored) that for both paths the remainder of the solution can be the same – since the constraints for the remainder of the solution are the same – so both paths are ruled out.

History

Slitherlink is an original puzzle of Nikoli; it first appeared in Puzzle Communication Nikoli #26 (June 1989). The editor combined two original puzzles contributed there. At first, every square contained a number and the edges did not have to form a loop.

Video games

Slitherlink puzzles have been featured in video games on several platforms. A game titled Slither Link was published in Japan by Bandai for the Wonderswan portable console in 2000.[1] Slitherlink puzzles were included alongside Sudoku and Nonogram puzzles in the Loppi Puzzle Magazine: Kangaeru Puzzle series of games from Success for the Game Boy Nintendo Power cartridge in 2001.[2] Slitherlink games were also featured for the Nintendo DS handheld game console, with Hudson Soft releasing Puzzle Series Vol. 5: Slitherlink in Japan on November 16, 2006, and Agetec including Slitherlink in its Nikoli puzzle compilation, Brain Buster Puzzle Pak, released in North America on June 17, 2007.[3]

See also

References

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.