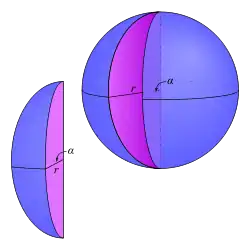
In geometry, a spherical wedge or ungula is a portion of a ball bounded by two plane semidisks and a spherical lune (termed the wedge's base). The angle between the radii lying within the bounding semidisks is the dihedral α. If AB is a semidisk that forms a ball when completely revolved about the z-axis, revolving AB only through a given α produces a spherical wedge of the same angle α.[1] Beman (2008)[2] remarks that "a spherical wedge is to the sphere of which it is a part as the angle of the wedge is to a perigon." [A] A spherical wedge of α = π radians (180°) is called a hemisphere, while a spherical wedge of α = 2π radians (360°) constitutes a complete ball.
The volume of a spherical wedge can be intuitively related to the AB definition in that while the volume of a ball of radius r is given by 4/3πr3, the volume a spherical wedge of the same radius r is given by[3]
Extrapolating the same principle and considering that the surface area of a sphere is given by 4πr2, it can be seen that the surface area of the lune corresponding to the same wedge is given by[A]
Hart (2009)[3] states that the "volume of a spherical wedge is to the volume of the sphere as the number of degrees in the [angle of the wedge] is to 360".[A] Hence, and through derivation of the spherical wedge volume formula, it can be concluded that, if Vs is the volume of the sphere and Vw is the volume of a given spherical wedge,
Also, if Sl is the area of a given wedge's lune, and Ss is the area of the wedge's sphere,[4][A]
See also
Notes
References
- ↑ Morton, P. (1830). Geometry, Plane, Solid, and Spherical, in Six Books. Baldwin & Cradock. p. 180.
- ↑ Beman, D. W. (2008). New Plane and Solid Geometry. BiblioBazaar. p. 338. ISBN 0-554-44701-0.
- 1 2 Hart, C. A. (2009). Solid Geometry. BiblioBazaar. p. 465. ISBN 1-103-11804-8.
- ↑ Avallone, E. A.; Baumeister, T.; Sadegh, A.; Marks, L. S. (2006). Marks' Standard Handbook for Mechanical Engineers. McGraw-Hill Professional. p. 43. ISBN 0-07-142867-4.