In mathematics, a split exact sequence is a short exact sequence in which the middle term is built out of the two outer terms in the simplest possible way.

Equivalent characterizations

A short exact sequence of abelian groups or of modules over a fixed ring, or more generally of objects in an abelian category

${\displaystyle 0\to A\mathrel {\stackrel {a}{\to }} B\mathrel {\stackrel {b}{\to }} C\to 0}$

is called split exact if it is isomorphic to the exact sequence where the middle term is the direct sum of the outer ones:

${\displaystyle 0\to A\mathrel {\stackrel {i}{\to }} A\oplus C\mathrel {\stackrel {p}{\to }} C\to 0}$

The requirement that the sequence is isomorphic means that there is an isomorphism ${\displaystyle f:B\to A\oplus C}$ such that the composite ${\displaystyle f\circ a}$ is the natural inclusion ${\displaystyle i:A\to A\oplus C}$ and such that the composite ${\displaystyle p\circ f}$ equals b. This can be summarized by a commutative diagram as:

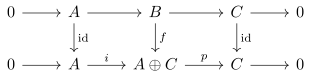
The splitting lemma provides further equivalent characterizations of split exact sequences.

Examples

A trivial example of a split short exact sequence is

${\displaystyle 0\to M_{1}\mathrel {\stackrel {q}{\to }} M_{1}\oplus M_{2}\mathrel {\stackrel {p}{\to }} M_{2}\to 0}$

where ${\displaystyle M_{1},M_{2}}$ are R-modules, ${\displaystyle q}$ is the canonical injection and ${\displaystyle p}$ is the canonical projection.

Any short exact sequence of vector spaces is split exact. This is a rephrasing of the fact that any set of linearly independent vectors in a vector space can be extended to a basis.

The exact sequence ${\displaystyle 0\to \mathbf {Z} \mathrel {\stackrel {2}{\to }} \mathbf {Z} \to \mathbf {Z} /2\to 0}$ (where the first map is multiplication by 2) is not split exact.

Related notions

Pure exact sequences can be characterized as the filtered colimits of split exact sequences.^[1]

References

Sources

• Fuchs, László (2015), Abelian Groups, Springer Monographs in Mathematics, Springer, ISBN 9783319194226
• Sharp, R. Y., Rodney (2001), Steps in Commutative Algebra, 2nd ed., London Mathematical Society Student Texts, Cambridge University Press, ISBN 0521646235