In geometry, a square trisection is a type of dissection problem which consists of cutting a square into pieces that can be rearranged to form three identical squares.

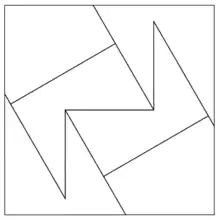
Square trisection using 6 pieces of same area (2010).

History

The dissection of a square in three congruent partitions is a geometrical problem that dates back to the Islamic Golden Age. Craftsman who mastered the art of zellige needed innovative techniques to achieve their fabulous mosaics with complex geometric figures. The first solution to this problem was proposed in the 10th century AD by the Persian mathematician Abu'l-Wafa' (940-998) in his treatise "On the geometric constructions necessary for the artisan".[1] Abu'l-Wafa' also used his dissection to demonstrate the Pythagorean theorem.[2] This geometrical proof of Pythagoras' theorem would be rediscovered in the years 1835 - 1840 [3] by Henry Perigal and published in 1875.[4]

Search of optimality

The beauty of a dissection depends on several parameters. However, it is usual to search for solutions with the minimum number of parts. Far from being minimal, the square trisection proposed by Abu'l-Wafa' uses 9 pieces. In the 14th century Abu Bakr al-Khalil gave two solutions, one of which uses 8 pieces.[5] In the late 17th century Jacques Ozanam came back to this issue [6] and in the 19th century, solutions using 8 and 7 pieces were found, including one given by the mathematician Édouard Lucas.[7] In 1891 Henry Perigal published the first known solution with only 6 pieces [8] (see illustration below). Nowadays, new dissections are still found [9] (see illustration above) and the conjecture that 6 is the minimal number of necessary pieces remains unproved.

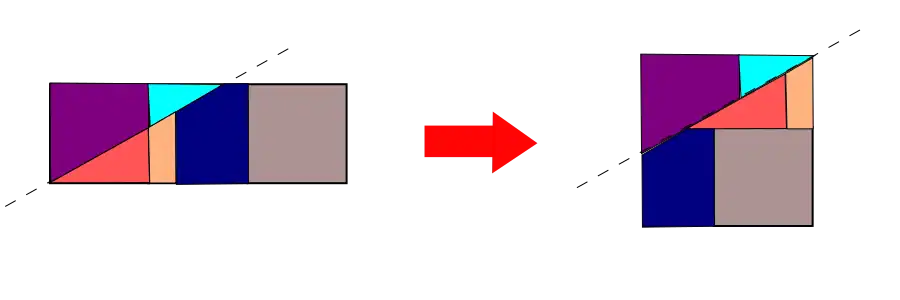
Henry Perigal (1891)

See also

Bibliography

  • Frederickson, Greg N. (1997). Dissections: Plane and Fancy. Cambridge University Press. ISBN 0-521-57197-9.
  • Frederickson, Greg N. (2002). Hinged Dissections: Swinging and Twisting. Cambridge University Press. ISBN 0-521-81192-9.
  • Frederickson, Greg N. (2006). Piano-hinged Dissections: Time to Fold!. en:A K Peters. ISBN 1-56881-299-X.

References

  1. ↑ Alpay Özdural (1995). Omar Khayyam, Mathematicians, and “conversazioni” with Artisans. Journal of the Society of Architectural Vol. 54, No. 1, Mar., 1995
  2. ↑ Reza Sarhangi, Slavik Jablan (2006). Elementary Constructions of Persian Mosaics. Towson University and The Mathematical Institute. online Archived 2011-07-28 at the Wayback Machine
  3. ↑ See appendix of L. J. Rogers (1897). Biography of Henry Perigal: On certain Regular Polygons in Modular Network. Proceedings London Mathematical Society. Volume s1-29, Appendix pp. 732-735.
  4. ↑ Henry Perigal (1875). On Geometric Dissections and Transformations, Messenger of Mathematics, No 19, 1875.
  5. ↑ Alpay Özdural (2000). Mathematics and Arts: Connections between Theory and Practice in the Medieval Islamic World, Historia Mathematica, Volume 27, Issue 2, May 2000, Pages 171-201.
  6. ↑ (fr) Jean-Etienne Montucla (1778), completed and re-edited by Jacques Ozanam (1640-1717) Récréations mathématiques, Tome 1 (1694), p. 297 Pl.15.
  7. ↑ (fr) Edouard Lucas (1883). Récréations Mathématiques, Volume 2. Paris, Gauthier-Villars. Second of four volumes. Second edition (1893) reprinted by Blanchard in 1960. See pp. 151 and 152 in Volume 2 of this edition. online (pp. 145-147).
  8. ↑ Henry Perigal (1891). Geometric Dissections and Transpositions, Association for the Improvement of Geometrical Teaching. wikisource
  9. ↑ Christian Blanvillain, János Pach (2010). Square Trisection. Bulletin d'Informatique Approfondie et Applications N°86 - Juin 2010 Archived 2011-07-24 at the Wayback Machine also at EPFL: oai:infoscience.epfl.ch:161493.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.