
In the mathematical theory of knots, the stick number is a knot invariant that intuitively gives the smallest number of straight "sticks" stuck end to end needed to form a knot. Specifically, given any knot , the stick number of , denoted by , is the smallest number of edges of a polygonal path equivalent to .
Known values
Six is the lowest stick number for any nontrivial knot. There are few knots whose stick number can be determined exactly. Gyo Taek Jin determined the stick number of a -torus knot in case the parameters and are not too far from each other:[1]
The same result was found independently around the same time by a research group around Colin Adams, but for a smaller range of parameters.[2]
Bounds
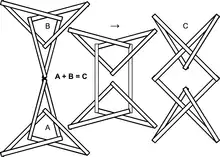
The stick number of a knot sum can be upper bounded by the stick numbers of the summands:[3]
Related invariants
The stick number of a knot is related to its crossing number by the following inequalities:[4]
These inequalities are both tight for the trefoil knot, which has a crossing number of 3 and a stick number of 6.
References
Notes
Introductory material
- Adams, C. C. (May 2001), "Why knot: knots, molecules and stick numbers", Plus Magazine. An accessible introduction into the topic, also for readers with little mathematical background.
- Adams, C. C. (2004), The Knot Book: An elementary introduction to the mathematical theory of knots, Providence, RI: American Mathematical Society, ISBN 0-8218-3678-1.
Research articles
- Adams, Colin C.; Brennan, Bevin M.; Greilsheimer, Deborah L.; Woo, Alexander K. (1997), "Stick numbers and composition of knots and links", Journal of Knot Theory and its Ramifications, 6 (2): 149–161, doi:10.1142/S0218216597000121, MR 1452436
- Calvo, Jorge Alberto (2001), "Geometric knot spaces and polygonal isotopy", Journal of Knot Theory and its Ramifications, 10 (2): 245–267, arXiv:math/9904037, doi:10.1142/S0218216501000834, MR 1822491
- Eddy, Thomas D.; Shonkwiler, Clayton (2019), New stick number bounds from random sampling of confined polygons, arXiv:1909.00917
- Jin, Gyo Taek (1997), "Polygon indices and superbridge indices of torus knots and links", Journal of Knot Theory and its Ramifications, 6 (2): 281–289, doi:10.1142/S0218216597000170, MR 1452441
- Negami, Seiya (1991), "Ramsey theorems for knots, links and spatial graphs", Transactions of the American Mathematical Society, 324 (2): 527–541, doi:10.2307/2001731, MR 1069741
- Huh, Youngsik; Oh, Seungsang (2011), "An upper bound on stick number of knots", Journal of Knot Theory and its Ramifications, 20 (5): 741–747, arXiv:1512.03592, doi:10.1142/S0218216511008966, MR 2806342
External links
- Weisstein, Eric W., "Stick number", MathWorld
- "Stick numbers for minimal stick knots", KnotPlot Research and Development Site.