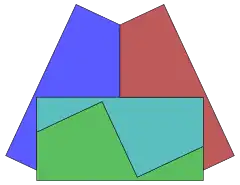
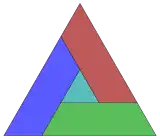
 Tetrad with one central region and 3 surrounding ones |
 Tetrad with a hole |
| Part of a series on |
| Puzzles |
|---|
 |
In geometry, a tetrad is a set of four simply connected disjoint planar regions in the plane, each pair sharing a finite portion of common boundary. It was named by Michael R. W. Buckley in 1975 in the Journal of Recreational Mathematics. A further question was proposed that became a puzzle, whether the 4 regions could be congruent, with or without holes, other enclosed regions.[1]
Fewest sides and vertices
The solutions with four congruent tiles include some with five sides.[2] However, their placement surrounds an uncovered hole in the plane. Among solutions without holes, the ones with the fewest possible sides are given by a hexagon identified by Scott Kim as a student at Stanford University.[1] It is not known whether five-sided solutions without holes are possible.[2]
Kim's solution has 16 vertices, while some of the pentagon solutions have as few as 11 vertices. It is not known whether fewer vertices are possible.[2]
Congruent polyform solutions
Gardner offered a number of polyform (polyomino, polyiamond, and polyhex) solutions, with no holes.[1]
 11 squares
11 squares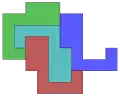 12 squares
12 squares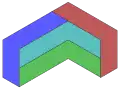 10 triangles
10 triangles 22 triangles
22 triangles 26 triangles
26 triangles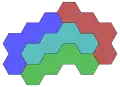 4 hexagons
4 hexagons
References
External links
- Polyform Tetrads and Polyomino and Polynar Tetrads
- A Tetrad Puzzle 7 April 2020
- Application of IT in Mathematical Proofs and in Checking of Results of Pupils’ Research
- Tetrads and their Counting Juris ČERŅENOKS, Andrejs CIBULIS