| Tetrakis cuboctahedron | |
|---|---|
 | |
| Type | Geodesic polyhedron (2,0) |
| Faces | 32 triangles (2 types) |
| Edges | 48 (2 types) |
| Vertices | 18 (2 types) |
| Vertex configuration | (6) 35 (12) 36 |
| Conway notation | k4aC |
| Symmetry group | Octahedral (Oh) |
| Dual polyhedron | chamfered cube |
| Properties | convex |
| Net | |
 | |
In geometry, the tetrakis cuboctahedron is a convex polyhedron with 32 triangular faces, 48 edges, and 18 vertices. It is a dual of the truncated rhombic dodecahedron.
Its name comes from a topological construction from the cuboctahedron with the kis operator applied to the square faces. In this construction, all the vertices are assumed to be the same distance from the center, while in general octahedral symmetry can be maintain even with the 6 order-4 vertices at a different distance from the center as the other 12.
Related polyhedra
It can also be topologically constructed from the octahedron, dividing each triangular face into 4 triangles by adding mid-edge vertices (an ortho operation). From this construction, all 32 triangles will be equilateral.
This polyhedron can be confused with a slightly smaller Catalan solid, the tetrakis hexahedron, which has only 24 triangles, 32 edges, and 14 vertices.
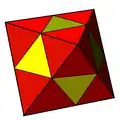Octahedron with edges bisected and faces divided into subtriangles of the tetrakis cuboctahedron
The nonconvex octahemioctahedron looks like a concave tetrakis cuboctahedron with inverted square pyramids meeting at the polyhedron center.
See also
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
- Chapter 21: Naming the Archimedean and Catalan polyhedra and Tilings (p284)
External links
- VTML polyhedral generator Try "k4aC" (Conway polyhedron notation)