 Involutional symmetry Cs, (*) [ ] = |
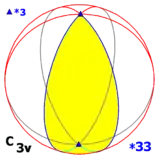 Cyclic symmetry Cnv, (*nn) [n] = |
 Dihedral symmetry Dnh, (*n22) [n,2] = | |
| Polyhedral group, [n,3], (*n32) | |||
|---|---|---|---|
 Tetrahedral symmetry Td, (*332) [3,3] = |
 Octahedral symmetry Oh, (*432) [4,3] = |
 Icosahedral symmetry Ih, (*532) [5,3] = | |
Finite spherical symmetry groups are also called point groups in three dimensions. There are five fundamental symmetry classes which have triangular fundamental domains: dihedral, cyclic, tetrahedral, octahedral, and icosahedral symmetry.
This article lists the groups by Schoenflies notation, Coxeter notation,[1] orbifold notation,[2] and order. John Conway uses a variation of the Schoenflies notation, based on the groups' quaternion algebraic structure, labeled by one or two upper case letters, and whole number subscripts. The group order is defined as the subscript, unless the order is doubled for symbols with a plus or minus, "±", prefix, which implies a central inversion.[3]
Hermann–Mauguin notation (International notation) is also given. The crystallography groups, 32 in total, are a subset with element orders 2, 3, 4 and 6.[4]
Involutional symmetry
There are four involutional groups: no symmetry (C1), reflection symmetry (Cs), 2-fold rotational symmetry (C2), and central point symmetry (Ci).
| Intl | Geo |
Orbifold | Schönflies | Conway | Coxeter | Order | Abstract | Fund. domain | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 11 | C1 | C1 | ][ [ ]+ | 1 | Z1 |  | |
| 2 | 2 | 22 | D1 = C2 |
D2 = C2 |
[2]+ | 2 | Z2 | 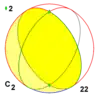 | |
| 1 | 22 | × | Ci = S2 |
CC2 | [2+,2+] | 2 | Z2 |  | |
| 2 = m |
1 | * | Cs = C1v = C1h |
±C1 = CD2 |
[ ] | 2 | Z2 |  | |
Cyclic symmetry
There are four infinite cyclic symmetry families, with n = 2 or higher. (n may be 1 as a special case as no symmetry)
| Intl | Geo |
Orbifold | Schönflies | Conway | Coxeter | Order | Abstract | Fund. domain | |
|---|---|---|---|---|---|---|---|---|---|
| 4 | 42 | 2× | S4 | CC4 | [2+,4+] | 4 | Z4 | 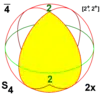 | |
| 2/m | 22 | 2* | C2h = D1d |
±C2 = ±D2 |
[2,2+] [2+,2] | 4 | Z4 | 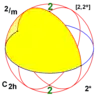 | |
| Intl | Geo |
Orbifold | Schönflies | Conway | Coxeter | Order | Abstract | Fund. domain | |
|---|---|---|---|---|---|---|---|---|---|
| 2 3 4 5 6 n |
2 3 4 5 6 n |
22 33 44 55 66 nn |
C2 C3 C4 C5 C6 Cn |
C2 C3 C4 C5 C6 Cn |
[2]+ [3]+ [4]+ [5]+ [6]+ [n]+ | 2 3 4 5 6 n |
Z2 Z3 Z4 Z5 Z6 Zn |
 | |
| 2mm 3m 4mm 5m 6mm nm (n is odd) nmm (n is even) |
2 3 4 5 6 n |
*22 *33 *44 *55 *66 *nn |
C2v C3v C4v C5v C6v Cnv |
CD4 CD6 CD8 CD10 CD12 CD2n |
[2] [3] [4] [5] [6] [n] | 4 6 8 10 12 2n |
D4 D6 D8 D10 D12 D2n |
 | |
| 3 8 5 12 - |
62 82 10.2 12.2 2n.2 |
3× 4× 5× 6× n× |
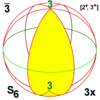
S6 S8 S10 S12 S2n |
±C3 CC8 ±C5 CC12 CC2n / ±Cn |
[2+,6+] [2+,8+] [2+,10+] [2+,12+] [2+,2n+] | 6 8 10 12 2n |
Z6 Z8 Z10 Z12 Z2n |
 | |
| 3/m=6 4/m 5/m=10 6/m n/m |
32 42 52 62 n2 |
3* 4* 5* 6* n* |
C3h C4h C5h C6h Cnh |
CC6 ±C4 CC10 ±C6 ±Cn / CC2n |
[2,3+] [2,4+] [2,5+] [2,6+] [2,n+] | 6 8 10 12 2n |
Z6 Z2×Z4 Z10 Z2×Z6 Z2×Zn ≅Z2n (odd n) |
 | |
Dihedral symmetry
There are three infinite dihedral symmetry families, with n = 2 or higher (n may be 1 as a special case).
| Intl | Geo |
Orbifold | Schönflies | Conway | Coxeter | Order | Abstract | Fund. domain |
|---|---|---|---|---|---|---|---|---|
| 222 | 2.2 | 222 | D2 | D4 | [2,2]+ |
4 | D4 |  |
| 42m | 42 | 2*2 | D2d | DD8 | [2+,4] |
8 | D4 | 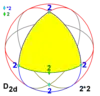 |
| mmm | 22 | *222 | D2h | ±D4 | [2,2] |
8 | Z2×D4 |  |
| Intl | Geo |
Orbifold | Schönflies | Conway | Coxeter | Order | Abstract | Fund. domain | |
|---|---|---|---|---|---|---|---|---|---|
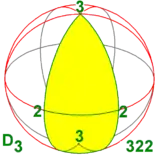
| 32 422 52 622 |
3.2 4.2 5.2 6.2 n.2 |
223 224 225 226 22n |
D3 D4 D5 D6 Dn |
D6 D8 D10 D12 D2n |
[2,3]+ [2,4]+ [2,5]+ [2,6]+ [2,n]+ | 6 8 10 12 2n |
D6 D8 D10 D12 D2n |
 | |
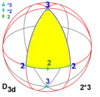
| 3m 82m 5m 12.2m |
62 82 10.2 12.2 n2 |
2*3 2*4 2*5 2*6 2*n |
D3d D4d D5d D6d Dnd |
±D6 DD16 ±D10 DD24 DD4n / ±D2n |
[2+,6] [2+,8] [2+,10] [2+,12] [2+,2n] | 12 16 20 24 4n |
D12 D16 D20 D24 D4n |
 | |
| 6m2 4/mmm 10m2 6/mmm |
32 42 52 62 n2 |
*223 *224 *225 *226 *22n |
D3h D4h D5h D6h Dnh |
DD12 ±D8 DD20 ±D12 ±D2n / DD4n |
[2,3] [2,4] [2,5] [2,6] [2,n] | 12 16 20 24 4n |
D12 Z2×D8 D20 Z2×D12 Z2×D2n ≅D4n (odd n) |
 | |
Polyhedral symmetry
There are three types of polyhedral symmetry: tetrahedral symmetry, octahedral symmetry, and icosahedral symmetry, named after the triangle-faced regular polyhedra with these symmetries.
| Intl | Geo |
Orbifold | Schönflies | Conway | Coxeter | Order | Abstract | Fund. domain |
|---|---|---|---|---|---|---|---|---|
| 23 | 3.3 | 332 | T | T | [3,3]+ |
12 | A4 | 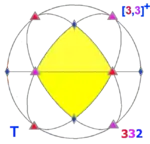 |
| m3 | 43 | 3*2 | Th | ±T | [4,3+] |
24 | 2×A4 | 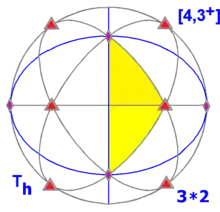 |
| 43m | 33 | *332 | Td | TO | [3,3] |
24 | S4 |  |
| Intl | Geo |
Orbifold | Schönflies | Conway | Coxeter | Order | Abstract | Fund. domain |
|---|---|---|---|---|---|---|---|---|
| 432 | 4.3 | 432 | O | O | [4,3]+ |
24 | S4 | 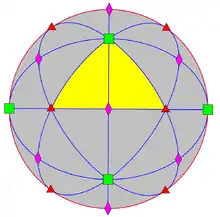 |
| m3m | 43 | *432 | Oh | ±O | [4,3] |
48 | 2×S4 |  |
| Intl | Geo |
Orbifold | Schönflies | Conway | Coxeter | Order | Abstract | Fund. domain |
|---|---|---|---|---|---|---|---|---|
| 532 | 5.3 | 532 | I | I | [5,3]+ |
60 | A5 | 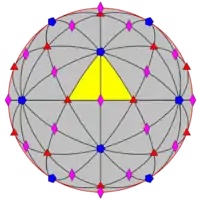 |
| 532/m | 53 | *532 | Ih | ±I | [5,3] |
120 | 2×A5 |  |
Continuous symmetries
All of the discrete point symmetries are subgroups of certain continuous symmetries. They can be classified as products of orthogonal groups O(n) or special orthogonal groups SO(n). O(1) is a single orthogonal reflection, dihedral symmetry order 2, Dih1. SO(1) is just the identity. Half turns, C2, are needed to complete.
| Rank 3 groups | Other names | Example geometry | Example finite subgroups | |
|---|---|---|---|---|
| O(3) | Full symmetry of the sphere |  | [3,3] = [4,3+] = | |
| SO(3) | Sphere group | Rotational symmetry | [3,3]+ = | |
| O(2)×O(1) O(2)⋊C2 | Dih∞×Dih1 Dih∞⋊C2 | Full symmetry of a spheroid, torus, cylinder, bicone or hyperboloid Full circular symmetry with half turn | 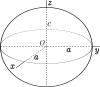 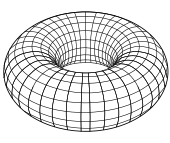 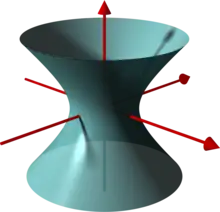 | [p,2] = [p]×[ ] = [2p,2+] = |
| SO(2)×O(1) | C∞×Dih1 | Rotational symmetry with reflection | [p+,2] = [p]+×[ ] = | |
| SO(2)⋊C2 | C∞⋊C2 | Rotational symmetry with half turn | [p,2]+ = | |
| O(2)×SO(1) | Dih∞ Circular symmetry | Full symmetry of a hemisphere, cone, paraboloid or any surface of revolution | .png.webp) .png.webp)  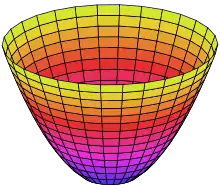 | [p,1] = [p] = |
| SO(2)×SO(1) | C∞ Circle group | Rotational symmetry | [p,1]+ = [p]+ = | |
See also
References
- ↑ Johnson, 2015
- ↑ Conway, John H. (2008). The symmetries of things. Wellesley, Mass: A.K. Peters. ISBN 978-1-56881-220-5. OCLC 181862605.
- ↑ Conway, John; Smith, Derek A. (2003). On quaternions and octonions: their geometry, arithmetic, and symmetry. Natick, Mass: A.K. Peters. ISBN 978-1-56881-134-5. OCLC 560284450.
- ↑ Sands, 1993
Further reading
- Peter R. Cromwell, Polyhedra (1997), Appendix I
- Sands, Donald E. (1993). "Crystal Systems and Geometry". Introduction to Crystallography. Mineola, New York: Dover Publications, Inc. p. 165. ISBN 0-486-67839-3.
- On Quaternions and Octonions, 2003, John Horton Conway and Derek A. Smith ISBN 978-1-56881-134-5
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN 978-1-56881-220-5
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
- N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, Table 11.4 Finite Groups of Isometries in 3-space