The tone clock, and its related compositional theory tone-clock theory, is a post-tonal music composition technique, developed by composers Peter Schat and Jenny McLeod. Music written using tone-clock theory features a high economy of musical intervals within a generally chromatic musical language. This is because tone-clock theory encourages the composer to generate all their harmonic and melodic material from a limited number of intervallic configurations (called "intervallic prime forms", or IPFs, in tone-clock terminology). Tone-clock theory is also concerned with the way that the three-note pitch-class sets (trichords or "triads" in tone-clock terminology) can be shown to underlie larger sets, and considers these triads as a fundamental unit in the harmonic world of any piece. Because there are twelve possible triadic prime forms, Schat called them the "hours", and imagined them arrayed in a clock face, with the smallest hour (012 or 1-1 in IPF notation) in the one o'clock position, and the largest hour (048 or 4-4 in IPF notation) in the 12 o'clock position. A notable feature of tone-clock theory is tone-clock steering: transposing or inverting hours so that each note of the chromatic aggregate is generated once and once only.
Relationship to pitch-class set theory and serialism
While tone-clock theory displays many similarities to Allen Forte's pitch-class set theory, it places greater emphasis on the creation of pitch fields from multiple transpositions and inversions of a single set-class, while also aiming to complete all twelve pitch-classes (the chromatic aggregate) with minimal, if any, repetition of pitch-classes. While the emphasis of tone-clock theory is on creating the chromatic aggregate, it is not a serial technique, as the ordering of pitch-classes is not important. However, it bears a certain similarity to the technique of serial derivation, which was used by Anton Webern and Milton Babbitt amongst others, in which a row is constructed from only one or two set-classes. It also bears a similarity to Josef Hauer's system of tropes, albeit generalised to sets of any cardinality.
Peter Schat
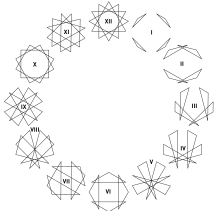
The term tone clock (toonklok in Dutch) was originally coined by Dutch composer Peter Schat, in reference to a technique he had developed of creating twelve-note pitch fields by transposing and inverting a trichord so that all twelve pitch-classes would be created once and once only.[1] Schat discovered that it was possible to achieve a trichordally partitioned aggregate from all twelve trichords, with the exception of the diminished triad (036 or 3-10 in Forte's pitch-class set theory). Schat called the 12 trichords the "hours", and they became central to the harmonic organization in a number of his works. He created a "zodiac" of the hours, which shows in graphical form the symmetrical patterns created by the tone-clock steerings of the hours. (Hour X is substituted with its tetrachord, the diminished seventh, which can be tone-clock steered).
Jenny McLeod
In her as-yet-unpublished monograph Chromatic Maps, New Zealand composer Jenny McLeod extended and expanded Schat's focus on trichords to encompass all 223 set-classes, thus becoming a true tone-clock theory.[2] She also introduced new terminology in order to "simplify" the labelling and categorization of the set-classes, and to draw attention to the specific transpositional properties within a field.
The most succinct musical expression of the theory is in her 24 Tone Clock Pieces, written between 1988–2011. Each of these piano works explores different aspects of tone-clock theory.
McLeod's terminology
The following terms are explained in McLeod's Chromatic Maps I:
- Intervallic prime form (IPF): the prime form of a pitch-class set, expressed as a series of interval classes (e.g. set-class (037) is called 3-4 in tone-clock theory, as these are the interval classes between successive pitches in the prime form). Where possible, IPFs is labelled using hour-group notation (see below). Furthermore, if an IPF can be rewritten so that the number of different interval classes in the title is one or two, then this is the preferred notation: e.g. IPF 143 (0158 in pc-set theory) can be rewritten as 414 or 434, which is to be preferred, as it makes the relationship to the trichords clearer.
- Hours: the 12 trichordal set-classes, called triads in tone-clock theory. The first hour is therefore IPF 1-1 (in pc-set theory, this would be set-class 3-1 or (012)), while the twelfth hour is IPF 4-4 (in pc-set theory, this would be set-class 3-12 or (048)). In tone-clock theory, the hours are often referred to using Roman numerals — so IV is IPF 1-4, while IX is IPF 2-5.
- Major and minor forms: For asymmetrical hours (hours that are formed from two different interval classes), the minor form is the inversion of the triad with the smallest ic on the bottom, while the major form is the inversion with the largest ic on the bottom. So, XIm is equivalent to a standard minor triad (3-4), while XIM is equivalent to a major triad (4-3).
- Hour groups: IPFs with only one or two interval classes can often be related to a single hour, and relabelled using the Roman numeral hour notation to make this relationship clear. For instance, the tetrachord IPF 242 clearly relates to the eighth hour, IPF 2-4 (set-class 3-8 in pc-set theory). It can therefore be labelled as VIII4 — the 4 relating to its cardinality, a tetrachord. Note that some IPFs cannot be labelled as hour-groups if the distribution of intervals is ambiguous: e.g. for IPF 2232, it is unclear as to whether the generating trichord is 2-2 (VI) or 2-3 (VII). However, 2232 can be rewritten as 3223, 5225 or 5555 or 2323, all of which are valid hour groups.
- Oedipus groups: The commonest kind of hour-group, in which two interval classes alternate (e.g. the octatonic scale, in which the interval classes proceed 1212121), relating to the second hour (II, or IPF 1-2). These are simply written in the form: II8.
- Multiple-hour groups: Some IPFs can be rearranged so that while they are no longer in prime form, they do display a different hour relationship — for instance, 414 (IVM4) can also be rewritten as 434 (XIM4). In tone-clock theory, this is considered to show that an IPF has multiple relationships to different hours, which can be brought out by the composer depending on how they are voiced and utilized.
- Symmetrical pentads: A pentachord/pentad that has a clear relationship to an asymmetrical hour, but in which the two interval classes are arrayed symmetrically rather than alternately (e.g. 2442) is called a 'symmetrical pentad', and is written thus: SP VIII.
- Steering: one IPF transposes by another (i.e. IPF a steers IPF b). If IPF a and b are the same, then this is self steering. Note that the IPF does not necessarily remain in its prime form, but can also appear inverted. In tone-clock theory, the steering group (the IPF that is underlying the transpositional levels) has a kind of deep structure status — the listener does not necessarily hear its immediate effect, but it governs elements such as voice-leadings.
- Reverse steering: the steering group becomes the steered group and vice versa — i.e. IPF b steers IPF A. In tone-clock theory, this is considered to have a kind of symmetry, and often appears to provide contrast or closure to a passage.
- Twelve-tone steering or tone-clock steering: a specific steering of an IPF so that the chromatic aggregate is created with no repetition of pc. All of the triads except the tenth hour (the diminished triad) can be steered in this way. Some tetrachords, and all hexachords that are self-complementary (i.e. not Z-related) can also be steered in this way.
- Anchor form: the creation of the twelve-tone aggregate with no pc repetition, typically from a tetrachord, but using a second IPF to complete the aggregate.
Mathematical generalizations of tessellating set-classes
New Zealand composer and music theorist Michael Norris has generalized the concept of tone-clock steering into a theory of pitch-class tessellation, and developed an algorithm that can provide tone-clock steerings, in 24TET. He has also written about and analyzed McLeod's tone clock pieces.[3][4]
References
- ↑ Schat, Peter (1993). Tone Clock (Contemporary Music Studies, vol. 7). Routledge.
- ↑ McLeod, Jenny (1994). "Chromatic Maps I & II". archive.org.
- ↑ Norris, Michael (2006). "Tessellations and Enumerations: generalizing chromatic theories". CANZONA: The Yearbook of the Composers Association of New Zealand: 92–100.
- ↑ Norris, Michael (2006). "Crystalline Aphorisms: commentary and analysis of Jenny McLeod's Tone Clock Pieces I–VII". Canzona: The Yearbook of the Composers Association of New Zealand: 74–86.