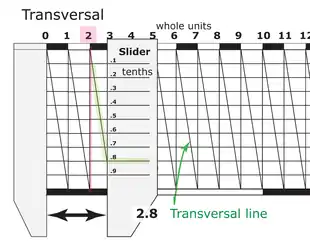
Transversal

Transversals are a geometric construction on a scientific instrument to allow a graduation to be read to a finer degree of accuracy. Their use creates what is sometimes called a diagonal scale, an engineering measuring instrument which is composed of a set of parallel straight lines which are obliquely crossed by another set of straight lines. Diagonal scales are used to measure small fractions of the unit of measurement.[1]

Transversals have been replaced in modern times by vernier scales. This method is based on the Intercept theorem (also known as Thales's theorem).

History

Transversals were used at a time when finely graduated instruments were difficult to make. They were found on instruments starting in the early 14th century, but the inventor is unknown. In 1342 Levi Ben Gerson introduced an instrument called Jacob's staff (apparently invented the previous century by Jacob Ben Makir) and described the method of the transversal scale applied to the mentioned instrument.[2][3]

Thomas Digges mistakenly attributed the discovery of the transversal scale to the navigator and explorer Richard Chancellor (cited by some authors as watchmaker and with other names, among them: Richard Chansler or Richard Kantzler).[4][5][6][7][8][9] Its use on astronomical instruments only began in the late 16th century. Tycho Brahe used them and did much to popularize the technique.[10][11] The technique began to die out once verniers became common in the late 18th century – over a century after Pierre Vernier introduced the technique.

In the interim between transversals and the vernier scale, the nonius system, developed by Pedro Nunes, was used. However, it was never in common use. Tycho also used nonius methods, but he appears to be the only prominent astronomer to do so.

Etymology

Diagonal scale is derived from the Latin word Diagonalis. The Latin word was originally coined from the Greek word diagōnios where dia means "through" and gonios denotes "corners".[1][12]

Principle of a diagonal scale

Diagonal scale follows the principle of similar triangles where a short length is divided into number of parts in which sides are proportional.[13] Divided into required number of equal parts

Linear transversals

Linear transversals
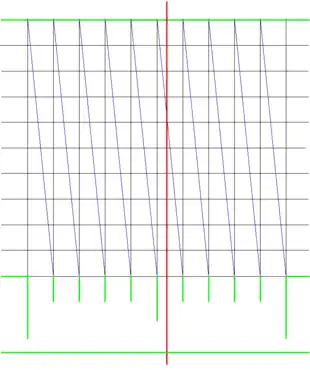
Black - grid lines
Blue - transversals
Green - instrument's graduations
Red - cursor line

Linear transversals were used on linear graduations. A grid of lines was constructed immediately adjacent to the linear graduations. The lines extending above the graduations formed part of the grid. The number of lines perpendicular to the extended graduation lines in the grid was dependent on the degree of fineness the instrument maker wished to provide.

A grid of five lines would permit determination of the measure to one-fifth of a graduation's division. A ten-line grid would permit tenths to be measured. The distance between the lines is not critical as long as the distance is precisely uniform. Greater distances makes for greater accuracy.

As seen in the illustration on the right, once the grid was scribed, diagonals (transverse lines) were scribed from the uppermost corner of a column in the grid to the opposite lowest corner. This line intersects the cross lines in the grid in equal intervals. By using an indicator such as a cursor or alidade, or by measuring using a pair of dividers with points on the same horizontal grid line, the closest point where the transversal crosses the grid is determined. That indicates the fraction of the graduation for the measure.

In the illustration, the reading is indicated by the vertical red line. This could be the edge of an alidade or a similar device. Since the cursor crosses the transversal closest to the fourth grid line from the top, the reading (assuming the leftmost long graduation line is 0.0) is 0.54.

Application

Diagonal scale is used in engineering to read lengths with higher accuracy as it represents a unit into three different multiple in metres, centimeters and millimeters.[14] Diagonal scale is an important part in Engineering drawings.[15]

Circular transversals

Circular transversals perform the same function as the linear ones but for circular arcs. In this case, the construction of the grid is significantly more complicated. A rectangular grid will not work. A grid of radial lines and circumferential arcs must be created. In addition, a linear transverse line will not divide the radial grid into equal segments. Circular arc segments must be constructed as transversals to provide the correct proportions.

Tycho Brahe

Tycho Brahe's transversal.

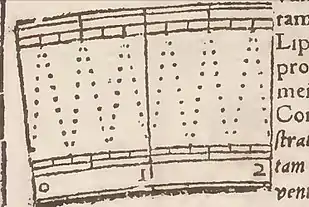
Tycho Brahe created a grid of transversal lines made with secants between two groups of arcs that form two graduated limbs. The secants are drawn by joining the division of a limb with the next division of the other limb, and so on (see figure with the magnification of 2 degrees of the Tycho Brahe's quadrant of 2m radius).[10]

He drew, for each degree, six straight transversals in an alternate mode forming a "V" and each transversal consisted of 9 points that divided it into 10 parts, which multiplied by 6 give 60 minutes.[16] While Abd al-Mun'im al 'Âmilî (16th century) drew them all in the same direction (although his instrument has less precision).[17]

Other authors

The method of the "straight transversals" applied to the measurements of angles on circular or semicircular limbs in astronomical and geographic instruments was treated by several authors. Studying the accuracy of the system, some of them indicated the convenience of employing "Circular transversals", instead of the "straight transversals".[18]

See also

References

  1. 1 2 Webster's Revised Unabridged Dictionary of the English Language: The Dictionary Proper Being the Authentic Ed. ... of 1890, to which is Now Added a Department of New Words Together with Many Valuable Special Features. Merriam-Webster. 1913.
  2. ↑ Bernard R. Goldstein (6 December 2012). The Astronomy of Levi ben Gerson (1288–1344): A Critical Edition of Chapters 1–20 with Translation and Commentary. Springer Science & Business Media. pp. 164–. ISBN 978-1-4613-8569-1.
  3. ↑ Brian Lasater (2008). The Dream of the West, Pt II. Lulu.com. pp. 355–. ISBN 978-1-4303-1382-3.
  4. ↑ Thomas Digges (1573). Alae seu scalae mathematicae, quibus visibilium remotissima coelorum theatra conscendi, & planetarum omnium itinera nouis & inauditis methodis explorari: ... Thoma Diggeseo, ... authore. pp. 86–.
  5. ↑ Joseph Needham (1959). Science and Civilisation in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Cambridge University Press. pp. 296–. ISBN 978-0-521-05801-8.
  6. ↑ Jean Baptiste Joseph Delambre (1819). Histoire de l'astronomie du moyen age; par m. Delambre, chevalier de Saint-Michel et de la Legion-d'honneur . mme ve Courcier, imprimeur-libraire pour les sciences. pp. 372–.
  7. ↑ Aimé Laussedat (1898). Recherches sur les instruments: Aperçu historique sur les instruments et les méthodes. La topographie dans tous les temps. Gauthier-Villars.
  8. ↑ Maurice Daumas (1953). Les Instruments scientifiques aux XVIIe et XVIIIe siècles. Presses Universitaires de France.
  9. ↑ A.D. Morrison-Low (2 March 2017). Making Scientific Instruments in the Industrial Revolution. Taylor & Francis. pp. 61–. ISBN 978-1-351-92074-2.
  10. 1 2 Tycho Brahe (1946). Tycho Brahe's description of his instruments and scientific work: as given in Astronomiae instauratae mechanica (Wandesburgi 1598). I Kommission hos E. Munksgaard.
  11. ↑ John Louis Emil Dreyer (13 February 2014). Tycho Brahe. Cambridge University Press. pp. 58–. ISBN 978-1-108-06871-0.
  12. ↑ Davidson, Thomas (1907). Chambers's Twentieth Century Dictionary of the English Language. W. & R. Chambers Limited.
  13. ↑ "Types of Scales in Engineering Surveying | Civil Engineering Projects". 28 October 2011. Retrieved 26 September 2016.
  14. ↑ Khan, Md Zulfequar Ahmad (1998). Text Book Of Practical Geography. Concept Publishing Company. p. 26. ISBN 9788170226826.
  15. ↑ Punmia, B. C. (2005). Surveying. Firewall Media. p. 11. ISBN 9788170088530. Retrieved 26 September 2016.
  16. ↑ Tycho Brahe (1602). Tychonis Brahe-Astronomiæ instauratæ mechanica. Noribergae [Nürnberg]: Levinum Hvlsivm.
  17. ↑ The Instruments of Istanbul Observatory (1977). The Instruments of Istanbul Observatory. p. 108.
  18. ↑ Allain Manesson-Mallet (1702). La Geometrie pratique: Tome second. Contenant la trigoniometrie, ou la mesure des distances par les instrumens geometriques ... chez Anisson directeur de l'Imprimerie Royale. pp. 32–.

Bibliography

  • Daumas, Maurice, Scientific Instruments of the Seventeenth and Eighteenth Centuries and Their Makers, Portman Books, London 1989 ISBN 978-0-7134-0727-3
  • Van Poelje, Otto E. (2004). "Diagonals and Transversals: Magnifying the Scale" (PDF). Journal of the Oughtred Society. 13 (2): 22–28.
Wikimedia Commons has media related to Nomograms.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.