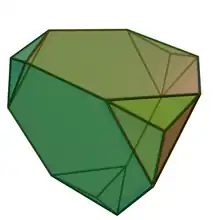
| Triakis truncated tetrahedron | |
|---|---|
 | |
| Type | Plesiohedron |
| Faces | 4 hexagons 12 isosceles triangles |
| Edges | 30 |
| Vertices | 16 |
| Conway notation | k3tT |
| Dual polyhedron | 16|Order-3 truncated triakis tetrahedron |
| Properties | convex |
In geometry, the triakis truncated tetrahedron is a convex polyhedron made from 4 hexagons and 12 isosceles triangles. It can be used to tessellate three-dimensional space, making the triakis truncated tetrahedral honeycomb.[1][2]
The triakis truncated tetrahedron is the shape of the Voronoi cell of the carbon atoms in diamond, which lie on the diamond cubic crystal structure.[3][4] As the Voronoi cell of a symmetric space pattern, it is a plesiohedron.[5]
Construction

Triakis truncated tetrahedral honeycomb
For space-filling, the triakis truncated tetrahedron can be constructed as follows:
- Truncate a regular tetrahedron such that the big faces are regular hexagons.
- Add an extra vertex at the center of each of the four smaller tetrahedra that were removed.
See also
References
- ↑ Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). The Symmetries of Things. p. 332. ISBN 978-1568812205.
- ↑ Grünbaum, B; Shephard, G. C. (1980). "Tilings with Congruent Tiles". Bull. Amer. Math. Soc. 3 (3): 951–973. doi:10.1090/s0273-0979-1980-14827-2.
- ↑ Föppl, L. (1914). "Der Fundamentalbereich des Diamantgitters". Phys. Z. 15: 191–193.
- ↑ Conway, John. "Voronoi Polyhedron". geometry.puzzles. Retrieved 20 September 2012.
- ↑ Grünbaum, Branko; Shephard, G. C. (1980), "Tilings with congruent tiles", Bulletin of the American Mathematical Society, New Series, 3 (3): 951–973, doi:10.1090/S0273-0979-1980-14827-2, MR 0585178.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.