Layers of Pascal's pyramid derived from coefficients in an upside-down ternary plot of the terms in the expansions of the powers of a trinomial – the number of terms is clearly a triangular number

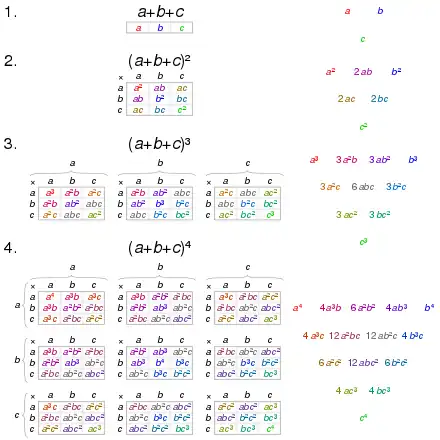
In mathematics, a trinomial expansion is the expansion of a power of a sum of three terms into monomials. The expansion is given by

${\displaystyle (a+b+c)^{n}=\sum _{{i,j,k} \atop {i+j+k=n}}{n \choose i,j,k}\,a^{i}\,b^{\;\!j}\;\!c^{k},}$

where n is a nonnegative integer and the sum is taken over all combinations of nonnegative indices i, j, and k such that i + j + k = n.^[1] The trinomial coefficients are given by

${\displaystyle {n \choose i,j,k}={\frac {n!}{i!\,j!\,k!}}\,.}$

This formula is a special case of the multinomial formula for m = 3. The coefficients can be defined with a generalization of Pascal's triangle to three dimensions, called Pascal's pyramid or Pascal's tetrahedron.^[2]

Derivation

The trinomial expansion can be calculated by applying the binomial expansion twice, setting ${\displaystyle d=b+c}$, which leads to

${\displaystyle {\begin{aligned}(a+b+c)^{n}&=(a+d)^{n}=\sum _{r=0}^{n}{n \choose r}\,a^{n-r}\,d^{r}\\&=\sum _{r=0}^{n}{n \choose r}\,a^{n-r}\,(b+c)^{r}\\&=\sum _{r=0}^{n}{n \choose r}\,a^{n-r}\,\sum _{s=0}^{r}{r \choose s}\,b^{r-s}\,c^{s}.\end{aligned}}}$

Above, the resulting ${\displaystyle (b+c)^{r}}$ in the second line is evaluated by the second application of the binomial expansion, introducing another summation over the index ${\displaystyle s}$.

The product of the two binomial coefficients is simplified by shortening ${\displaystyle r!}$,

${\displaystyle {n \choose r}\,{r \choose s}={\frac {n!}{r!(n-r)!}}{\frac {r!}{s!(r-s)!}}={\frac {n!}{(n-r)!(r-s)!s!}},}$

and comparing the index combinations here with the ones in the exponents, they can be relabelled to ${\displaystyle i=n-r,~j=r-s,~k=s}$, which provides the expression given in the first paragraph.

Properties

The number of terms of an expanded trinomial is the triangular number

${\displaystyle t_{n+1}={\frac {(n+2)(n+1)}{2}},}$

where n is the exponent to which the trinomial is raised.^[3]

Example

An example of a trinomial expansion with ${\displaystyle n=2}$ is :

${\displaystyle (a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2ab+2bc+2ca}$

See also

• Binomial expansion
• Pascal's pyramid
• Multinomial coefficient
• Trinomial triangle

References