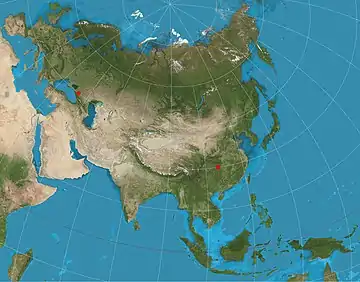

The two-point equidistant projection or doubly equidistant projection is a map projection first described by Hans Maurer in 1919 and Charles Close in 1921.[1][2] It is a generalization of the much simpler azimuthal equidistant projection. In this two-point form, two locus points are chosen by the mapmaker to configure the projection. Distances from the two loci to any other point on the map are correct: that is, they scale to the distances of the same points on the sphere.
The two-point equidistant projection maps a family of confocal spherical conics onto two families of planar ellipses and hyperbolas.[3]
The projection has been used for all maps of the Asian continent by the National Geographic Society atlases since 1959,[4] though its purpose in that case was to reduce distortion throughout Asia rather than to measure from the two loci.[5] The projection sometimes appears in maps of air routes. The Chamberlin trimetric projection is a logical extension of the two-point idea to three points, but the three-point case only yields a sort of minimum error for distances from the three loci, rather than yielding correct distances. Tobler extended this idea to arbitrarily large number of loci by using automated root-mean-square minimization techniques rather than using closed-form formulae.[6]
The projection can be generalized to an ellipsoid of revolution by using geodesic distance.[7]
See also
References
- ↑ Hans Maurer (1919). „Doppelbüschelstrahlige, orthodromische“ statt „doppelazimutale, gnomonische“ Kartenentwürfe. Doppel-mittabstandstreue Kartogramme. (Bemerkungen zu den Aufsätzen von W. Immler und H. Thorade. Ann. d. Hydr. usw 1919, S. 22 und 35.), Annalen der Hydrographie und Maritimen Meteorologie, 47 (3–4), 75–8.
- ↑ Charles Close (1921). “Note on a doubly-equidistant projection.” The Geographical Journal 57(6), 446–448. https://www.jstor.org/stable/1780793
- ↑ J.F. Cox (1946) “The doubly equidistant projection”. Bull. Geodesique 2, 74–76. https://doi.org/10.1007/BF02521618
- ↑ Snyder, J.P. (1993). Flattening the Earth: 2,000 years of map projections. pp. 234–235. ISBN 0226767469.
- ↑ "Portrait of Earth's largest continent", National Geographic Magazine, vol. 116, no. 6, p. 751, 1959
- ↑ Tobler, Waldo (April 1986). "Measuring the Similarity of Map Projections". Cartography and Geographic Information Science. 13 (2): 135–139. doi:10.1559/152304086783900103 – via Researchgate.
- ↑ Charles Karney, (2011). “Geodesics on an ellipsoid of revolution”. https://arxiv.org/abs/1102.1215
- Charles Close (1934). “A doubly equidistant projection of the sphere.” The Geographical Journal 83(2): 144-145.
- Charles Close (1947). Geographical By-ways: And Some Other Geographical Essays. E. Arnold.
- Waldo R. Tobler (1966). “Notes on two projections.” The Cartographic Journal 3(2). 87–89.
- François Reignier (1957). Les systèmes de projection et leurs applications a la géographie, a la cartographie, a la navigation, a la topométrie, etc... Institut géographique national.