The unified strength theory (UST).^[1][2][3][4] proposed by Yu Mao-Hong is a series of yield criteria (see yield surface) and failure criteria (see Material failure theory). It is a generalized classical strength theory which can be used to describe the yielding or failure of material begins when the combination of principal stresses reaches a critical value.^[5][6][7]

Mathematical Formulation

Mathematically, the formulation of UST is expressed in principal stress state as

${\displaystyle F={\sigma _{1}}-{\frac {\alpha }{1+b}}(b{\sigma _{2}}+{\sigma _{3}})={\sigma _{t}},\,{\text{ when }}{\sigma _{2}}\leqslant {\frac {{\sigma _{1}}+\alpha {\sigma _{3}}}{1+\alpha }}}$

${\displaystyle F'={\frac {1}{1+b}}({\sigma _{1}}+b{\sigma _{3}})-\alpha {\sigma _{3}}={\sigma _{t}},\,{\text{ when }}{\sigma _{2}}\geqslant {\frac {{\sigma _{1}}+\alpha {\sigma _{3}}}{1+\alpha }}}$

where ${\displaystyle {\sigma _{1}},{\sigma _{2}},{\sigma _{3}}}$ are three principal stresses, ${\displaystyle {\sigma _{t}}}$is the uniaxial tensile strength and ${\displaystyle \alpha }$ is tension-compression strength ratio (${\displaystyle \alpha ={\sigma _{t}}/{\sigma _{c}}}$). The unified yield criterion (UYC) is the simplification of UST when ${\displaystyle \alpha =1}$, i.e.

${\displaystyle f={\sigma _{1}}-{\frac {1}{1+b}}(b{\sigma _{2}}+{\sigma _{3}})={\sigma _{s}},{\text{ when }}{\sigma _{2}}\leqslant {\frac {1}{2}}({\sigma _{1}}+{\sigma _{3}})}$

${\displaystyle f'={\frac {1}{1+b}}({\sigma _{1}}+b{\sigma _{2}})-{\sigma _{3}}={\sigma _{s}},{\text{ when }}{\sigma _{2}}\geqslant {\frac {1}{2}}({\sigma _{1}}+{\sigma _{3}})}$

Limit surfaces of Unified Strength Theory

The limit surfaces of the unified strength theory in principal stress space are usually a semi-infinite dodecahedron cone with unequal sides. The shape and size of the limiting dodecahedron cone depends on the parameter b and ${\displaystyle \alpha }$. The limit surfaces of UST and UYC are shown as follows.

The limit surfaces of UST with ${\displaystyle \alpha }$=0.6

The limit surfaces of UYC

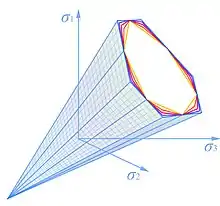
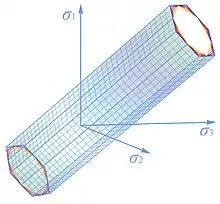
Derivation of Unified Strength Theory

Due to the relation (${\displaystyle {\tau _{13}}={\tau _{12}}+{\tau _{23}}}$), the principal stress state (${\displaystyle {\sigma _{1}},{\sigma _{2}},{\sigma _{3}}}$) may be converted to the twin-shear stress state (${\displaystyle {\tau _{13}},{\tau _{12}};{\sigma _{13}},{\sigma _{12}}}$) or (${\displaystyle {\tau _{13}},{\tau _{23}};{\sigma _{13}},{\sigma _{23}}}$). Twin-shear element models proposed by Mao-Hong Yu are used for representing the twin-shear stress state.^[1] Considering all the stress components of the twin-shear models and their different effects yields the unified strength theory as

${\displaystyle F={\tau _{13}}+b{\tau _{12}}+\beta ({\sigma _{13}}+b{\sigma _{12}})=C,{\text{ when }}{\tau _{12}}+\beta {\sigma _{12}}\geqslant {\tau _{23}}+\beta {\sigma _{23}}}$

${\displaystyle F'={\tau _{13}}+b{\tau _{23}}+\beta ({\sigma _{13}}+b{\sigma _{23}})=C,{\text{ when }}{\tau _{12}}+\beta {\sigma _{12}}\leqslant {\tau _{23}}+\beta {\sigma _{23}}}$

The relations among the stresses components and principal stresses read

${\displaystyle {\tau _{13}}={\frac {1}{2}}\left({{\sigma _{1}}-{\sigma _{3}}}\right)}$, ${\displaystyle {\sigma _{13}}={\frac {1}{2}}\left({{\sigma _{1}}+{\sigma _{3}}}\right)}$

${\displaystyle {\tau _{12}}={\frac {1}{2}}\left({{\sigma _{1}}-{\sigma _{2}}}\right)}$, ${\displaystyle {\sigma _{12}}={\frac {1}{2}}\left({{\sigma _{1}}+{\sigma _{2}}}\right)}$

${\displaystyle {\tau _{23}}={\frac {1}{2}}\left({{\sigma _{2}}-{\sigma _{3}}}\right)}$, ${\displaystyle {\sigma _{23}}={\frac {1}{2}}\left({{\sigma _{2}}+{\sigma _{3}}}\right)}$

The ${\displaystyle \beta }$ and C should be obtained by uniaxial failure state

${\displaystyle {\sigma _{1}}={\sigma _{t}},{\sigma _{2}}={\sigma _{3}}=0}$

${\displaystyle {\sigma _{1}}={\sigma _{2}}=0,{\sigma _{3}}=-{\sigma _{\text{c}}}}$

By substituting Eqs.(4a), (4b) and (5a) into the Eq.(3a), and substituting Eqs.(4a), (4c) and (5b) into Eq.(3b), the ${\displaystyle \beta }$ and C are introduced as

${\displaystyle \beta ={\frac {{\sigma _{\text{c}}}-{\sigma _{\text{t}}}}{{\sigma _{\text{c}}}+{\sigma _{\text{t}}}}}={\frac {1-\alpha }{1+\alpha }}}$, ${\displaystyle C={\frac {1+b{\sigma _{\text{c}}}{\sigma _{\text{t}}}}{{\sigma _{\text{c}}}+{\sigma _{\text{t}}}}}={\frac {1+b}{1+\alpha }}{\sigma _{t}}}$

History of Unified Strength Theory

The development of the unified strength theory can be divided into three stages as follows.
1. Twin-shear yield criterion (UST with ${\displaystyle \alpha =1}$ and ${\displaystyle b=1}$)^[8][9]

${\displaystyle f={\sigma _{1}}-{\frac {1}{2}}({\sigma _{2}}+{\sigma _{3}})={\sigma _{t}},{\text{ when }}{\sigma _{2}}\leqslant {\frac {{\sigma _{1}}+{\sigma _{3}}}{2}}}$

${\displaystyle f={\frac {1}{2}}({\sigma _{1}}+{\sigma _{2}})-{\sigma _{3}}={\sigma _{t}},{\text{ when }}{\sigma _{2}}\geqslant {\frac {{\sigma _{1}}+{\sigma _{3}}}{2}}}$

2. Twin-shear strength theory (UST with ${\displaystyle b=1}$)^[10].

${\displaystyle F={\sigma _{1}}-{\frac {\alpha }{2}}({\sigma _{2}}+{\sigma _{3}})={\sigma _{t}},{\text{ when }}{\sigma _{2}}\leqslant {\frac {{\sigma _{1}}+\alpha {\sigma _{3}}}{1+\alpha }}}$

${\displaystyle F={\frac {1}{2}}({\sigma _{1}}+{\sigma _{2}}){\text{ - }}\alpha {\sigma _{3}}={\sigma _{t}},{\text{ when }}{\sigma _{2}}\geqslant {\frac {{\sigma _{1}}+\alpha {\sigma _{3}}}{1+\alpha }}}$

3. Unified strength theory^[1].

Applications of the Unified Strength theory

Unified strength theory has been used in Generalized Plasticity,^[11] Structural Plasticity,^[12] Computational Plasticity^[13] and many other fields^[14][15]

References