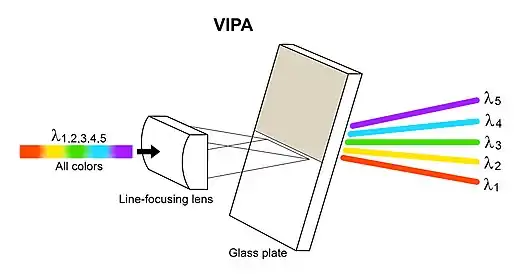
A virtually imaged phased array (VIPA) is an angular dispersive device that, like a prism or a diffraction grating, splits light into its spectral components. The device works almost independently of polarization. In contrast to prisms or regular diffraction gratings, the VIPA has a much higher angular dispersion but has a smaller free spectral range. This aspect is similar to that of an Echelle grating, since it also uses high diffraction orders. To overcome this disadvantage, the VIPA can be combined with a diffraction grating. The VIPA is a compact spectral disperser with high wavelength resolving power.
Basic mechanism
In a virtually imaged phased array, the phased array is the optical analogue of a phased array antenna at radio frequencies. Unlike a diffraction grating which can be interpreted as a real phased array, in a virtually imaged phased array the phased array is created in a virtual image. More specifically, the optical phased array is virtually formed with multiple virtual images of a light source. This is the fundamental difference from an Echelle grating, where a similar phased array is formed in the real space. The virtual images of a light source in the VIPA are automatically aligned exactly at a constant interval, which is critical for optical interference. This is an advantage of the VIPA over an Echelle grating. When the output light is observed, the virtually imaged phased array works as if light were emitted from a real phased array.
History and applications
VIPA was proposed and named by Shirasaki in 1996.[1] Prior to the publication in the paper, a preliminary presentation was given by Shirasaki at a conference.[2] This presentation was reported in Laser Focus World.[3] The details of this new approach to producing angular dispersion were described in the patent.[4] Since then, in the first ten years, the VIPA was of particular interest in the field of optical fiber communication technology. The VIPA was first applied to optical wavelength division multiplexing (WDM) and a wavelength demultiplexer was demonstrated for a channel spacing of 0.8 nm,[1] which was a standard channel spacing at the time. Later, a much smaller channel separation of 24 pm and a 3 dB bandwidth of 6 pm were achieved by Weiner in 2005 at 1550 nm wavelength range.[5] For another application, by utilizing the wavelength-dependent length of the light path due to the angular dispersion of the VIPA, the compensation of chromatic dispersion of fibers was studied and demonstrated (Shirasaki, 1997).[6][7] The compensation was further developed for tunable systems by using adjustable mirrors[8][9][10] or a spatial light modulator (Weiner, 2006).[11] Using the VIPA, compensation of polarization mode dispersion was also achieved (Weiner, 2008).[12] Furthermore, pulse shaping using the combination of a VIPA for high-resolution wavelength splitting/recombining and a SLM was demonstrated (Weiner, 2010).[13]
A drawback of the VIPA is its limited free spectral range due to the high diffraction order. To expand the functional wavelength range, Shirasaki combined a VIPA with a regular diffraction grating in 1997 to provide a broadband two-dimensional spectral disperser.[14] This configuration can be a high performance substitute for diffraction gratings in many grating applications. After the mid 2000s, the two-dimensional VIPA disperser has been used in various fields and devices, such as high-resolution WDM (Weiner, 2004),[15] a laser frequency comb (Diddams, 2007),[16] a spectrometer (Nugent-Glandorf, 2012),[17] an astrophysical instrument (Le Coarer, 2017),[18] Brillouin spectroscopy in biomechanics (Scarcelli, 2008, Rosa, 2018, and Margueritat, 2020),[19][20][21] other Brillouin spectroscopy (Loubeyre, 2022 and Wu, 2023),[22][23] beam scanning (Ford, 2008),[24] microscopy (Jalali, 2009),[25] tomography imaging (Ellerbee, 2014),[26] metrology (Bhattacharya, 2015),[27] fiber laser (Xu, 2020),[28] LiDAR (Fu, 2021),[29] and surface measurement (Zhu, 2022).[30]
Structure and operational principle
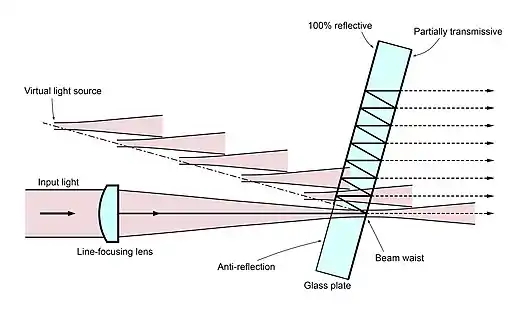
The main component of a VIPA is a glass plate whose normal is slightly tilted with respect to the input light. One side (light input side) of the glass plate is coated with a 100% reflective mirror and the other side (light output side) is coated with a highly reflective but partially transmissive mirror. The side with the 100% reflective mirror has an anti-reflection coated light entrance area, through which a light beam enters the glass plate. The input light is line-focused to a line (focal line) on the partially transmissive mirror on the light output side. A typical line-focusing lens is a cylindrical lens, which is also part of the VIPA. The light beam is diverging after the beam waist located at the line-focused position.
After the light enters the glass plate through the light entrance area, the light is reflected at the partially transmissive mirror and the 100% reflective mirror, and thus the light travels back and forth between the partially transmissive mirror and the 100% reflective mirror.
It is noted that the glass plate is tilted as a result of its slight rotation where the axis of rotation is the focal line. This rotation/tilt prevents the light from leaving the glass plate out of the light entrance area. Therefore, in order for the optical system to work as a VIPA, there is a critical minimum angle of tilt that allows the light entering through the light entrance area to return only to the 100% reflective mirror.[1] Below this angle, the function of the VIPA is severely impaired. If the tilting angle were zero, the reflected light from the partially transmissive mirror would travel exactly in reverse and exit the glass plate through the light entrance area without being reflected by the 100% reflective mirror. In the figure, refraction at the surfaces of the glass plate was ignored for simplicity.[1]
When the light beam is reflected each time at the partially transmissive mirror, a small portion of the light power passes through the mirror and travels away from the glass plate. For a light beam passing through the mirror after multiple reflections, the position of the line-focus can be seen in the virtual image when observed from the light output side. Therefore, this light beam travels as if it originated at a virtual light source located at the position of the line-focus and diverged from the virtual light source. The positions of the virtual light sources for all the transmitted light beams automatically align along the normal to the glass plate with a constant spacing, that is, a number of virtual light sources are superimposed to create an optical phased array. Due to the interference of all the light beams, the phased array emits a collimated light beam in one direction, which is at a wavelength dependent angle, and therefore, an angular dispersion is produced.
Wavelength resolution
Similarly to the resolving power of a diffraction grating, which is determined by the number of the illuminated grating elements and the order of diffraction, the resolving power of a VIPA is determined by the reflectivity of the back surface of the VIPA and the thickness of the glass plate. For a fixed thickness, a high reflectivity causes light to stay longer in the VIPA. This creates more virtual sources of light and thus increases the resolving power. On the other hand, with a lower reflectivity, the light in the VIPA is quickly lost, meaning fewer virtual sources of light are superimposed. This results in lower resolving power.
For large angular dispersion with high resolving power, the dimensions of the VIPA should be accurately controlled. Fine tuning of the VIPA characteristics was demonstrated by developing an elastomer-based structure (Metz, 2013).[31]
A constant reflectivity of the partially transmissive mirror in the VIPA produces a Lorentzian power distribution when the output light is imaged onto a screen, which has a negative effect on the wavelength selectivity. This can be improved by providing the partially transmissive mirror with a linearly decreasing reflectivity. This leads to a Gaussian-like power distribution on a screen and improves the wavelength selectivity or the resolving power.[32]
Spectral dispersion law
An analytical calculation of the VIPA was first performed by Vega and Weiner in 2003 [33] based on the theory of plane waves and an improved model based on the Fresnel diffraction theory was developed by Xiao and Weiner in 2004.[34]
Commercialization of the VIPA
VIPA devices have been commercialized by LightMachinery as spectral disperser devices or components with various customized design parameters.
References
- 1 2 3 4 Shirasaki, M. (1996). "Large angular dispersion by a virtually imaged phased array and its application to a wavelength demultiplexer". Optics Letters. 21 (5): 366–8. Bibcode:1996OptL...21..366S. doi:10.1364/OL.21.000366. PMID 19865407.
- ↑ Shirasaki, M. (October 1995). Large angular-dispersion by virtually-imaged phased-array (VIPA) and its application to wavelength demultiplexing. 5th Microoptics Conference (MOC'95). Hiroshima, Japan. Paper PD3.
- ↑ "Virtual imaging array splits light into ten wavelengths". Laser Focus World. 31 (12): 30–33. December 1995.
- ↑ US patent 5,999,320, Shirasaki, M., "Virtually imaged phased array as a wavelength demultiplexer"
- ↑ Xiao, S.; Weiner, A. M. (2005). "An eight-channel hyperfine wavelength demultiplexer using a virtually imaged phased-array (VIPA)". IEEE Photonics Technology Letters. 17 (2): 372. Bibcode:2005IPTL...17..372X. doi:10.1109/LPT.2004.839017. S2CID 37277234.
- ↑ Shirasaki, M. (1997). "Chromatic-dispersion compensator using virtually imaged phased array". IEEE Photonics Technology Letters. 9 (12): 1598–1600. Bibcode:1997IPTL....9.1598S. doi:10.1109/68.643280. S2CID 25043474.
- ↑ Shirasaki, M.; Cao, S. (March 2001). Compensation of chromatic dispersion and dispersion slope using a virtually imaged phased array. 2001 Optical Fiber Communication Conference. Anaheim, CA. Paper TuS1.
- ↑ Shirasaki, M.; Kawahata, Y.; Cao, S.; Ooi, H.; Mitamura, N.; Isono, H.; Ishikawa, G.; Barbarossa, G.; Yang, C.; Lin, C. (September 2000). Variable dispersion compensator using the virtually imaged phased array (VIPA) for 40-Gbit/s WDM transmission systems. 2000 European Conference on Optical Communication. Munich, Germany. Paper PD-2.3.
- ↑ Garrett, L. D.; Gnauck, A. H.; Eiselt, M. H.; Tkach, R. W.; Yang, C.; Mao, C.; Cao, S. (March 2000). Demonstration of virtually-imaged phased-array device for tunable dispersion compensation in 16 X10 Gb/s WDM transmission over 480 km standard fiber. 2000 Optical Fiber Communication Conference. Baltimore, MD. Paper PD7.
- ↑ Cao, S.; Lin, C.; Barbarossa, G.; Yang, C. (July 2001). Dynamically tunable dispersion slope compensation using a virtually imaged phased array (VIPA). 2001 LEOS Summer Topical Meetings Tech. Dig. Copper Mountain, CO.
- ↑ Lee, G-H; Xiao, S.; Weiner, A. M. (2006). "Optical dispersion compensator with >4000-ps/nm tuning range using a virtually imaged phased array (VIPA) and spatial light modulator (SLM)". IEEE Photonics Technology Letters. 18 (17): 1819. Bibcode:2006IPTL...18.1819L. doi:10.1109/LPT.2006.880732. S2CID 2418483.
- ↑ Miao, H.; Weiner, A. M.; Mirkin, L.; Miller, P. J. (2008). "AII-order polarization-mode dispersion (PMD) compensation via virtually imaged phased array (VIPA) - based pulse shaper". IEEE Photonics Technology Letters. 20 (8): 545. Bibcode:2008IPTL...20..545M. doi:10.1109/LPT.2008.918893. S2CID 26711798.
- ↑ Supradeepa, V. R.; Hamidi, E.; Leaird, D. E.; Weiner, A. M. (2010). "New aspects of temporal dispersion in high resolution Fourier pulse shaping: A quantitative description with virtually imaged phased array pulse shapers". Journal of the Optical Society of America B. 27 (9): 1833. arXiv:1004.4693. Bibcode:2010JOSAB..27.1833S. doi:10.1364/JOSAB.27.001833. S2CID 15594268.
- ↑ US patent 5,973,838, Shirasaki, M., "Apparatus which includes a virtually imaged phased array (VIPA) in combination with a wavelength splitter to demultiplex wavelength division multiplexed (WDM) light"
- ↑ Xiao, S.; Weiner, A. W. (2004). "2-D wavelength demultiplexer with potential for >1000 channels in the C-band" (PDF). Optics Express. 12 (13): 2895–902. Bibcode:2004OExpr..12.2895X. doi:10.1364/OPEX.12.002895. PMID 19483805. S2CID 22626277.
- ↑ Diddams, S. A.; Hollberg, L.; Mbele, V. (2007). "Molecular fingerprinting with the resolved modes of a femtosecond laser frequency comb". Nature. 445 (7128): 627–630. doi:10.1038/nature05524. PMID 17287805. S2CID 4420945.
- ↑ Nugent-Glandorf, L.; Neely, T.; Adler, F.; Fleisher, A. J.; Cossel, K. C.; Bjork, B.; Dinneen, T.; Ye, J.; Diddams, S. A. (2012). "Mid-infrared virtually imaged phased array spectrometer for rapid and broadband trace gas detection". Optics Letters. 37 (15): 3285–7. arXiv:1206.1316. Bibcode:2012OptL...37.3285N. doi:10.1364/OL.37.003285. PMID 22859160. S2CID 16831767.
- ↑ Bourdarot, G.; Coarer, E. L.; Bonfils, X.; Alecian, E.; Rabou, P.; Magnard, Y. (2017). "NanoVipa: a miniaturized high-resolution echelle spectrometer, for the monitoring of young stars from a 6U Cubesat". CEAS Space Journal. 9 (4): 411. Bibcode:2017CEAS....9..411B. doi:10.1007/s12567-017-0168-2. S2CID 125787048.
- ↑ Scarcelli, G.; Yun, S. H. (2008). "Confocal Brillouin microscopy for three-dimensional mechanical imaging". Nature Photonics. 2 (1): 39–43. Bibcode:2008NaPho...2...39S. doi:10.1038/nphoton.2007.250. PMC 2757783. PMID 19812712.
- ↑ Antonacci, G.; de Turris, V.; Rosa, A.; Ruocco, G. (2018). "Background-deflection Brillouin microscopy reveals altered biomechanics of intracellular stress granules by ALS protein FUS". Communications Biology. 10 (139): 139. doi:10.1038/s42003-018-0148-x. PMC 6131551. PMID 30272018.
- ↑ Yan, G; Bazir, A; Margueritat, J; Dehoux, T (2020). "Evaluation of commercial virtually imaged phase array and Fabry-Pérot based Brillouin spectrometers for applications to biology". Biomedical Optics Express. 11 (12): 6933–6944. doi:10.1364/BOE.401087. PMC 7747923.
- ↑ Forestier, A; Weck, G; Datchi, F; Loubeyre, P (2022). "Performances of a VIPA-based spectrometer for Brillouin scattering experiments in the diamond anvil cell under laser heating". High Pressure Research. 42 (3): 259–277. doi:10.1080/08957959.2022.2109968.
- ↑ Salzenstein, P; Wu, T (2023). "Uncertainty estimation for the Brillouin frequency shift measurement using a scanning tandem Fabry–Pérot interferometer". Micromachines. 14. doi:10.3390/mi14071429. PMC 10386179.
- ↑ Chan, T.; Myslivet, E.; Ford, J. E. (2008). "2-Dimensional beamsteering using dispersive deflectors and wavelength tuning". Optics Express. 16 (19): 14617–28. Bibcode:2008OExpr..1614617C. doi:10.1364/OE.16.014617. PMID 18794998.
- ↑ Tsia, K. K.; Goda, K.; Capewell, D.; Jalali, B. (2009). "Simultaneous mechanical-scan-free confocal microscopy and laser microsurgery". Optics Letters. 34 (14): 2099–101. Bibcode:2009OptL...34.2099T. doi:10.1364/OL.34.002099. hdl:10722/91309. PMID 19823514. S2CID 6265532.
- ↑ Lee, H. Y.; Marvdashti, T.; Duan, L.; Khan, S. A.; Ellerbee, A. K. (2014). "Scalable multiplexing for parallel imaging with interleaved optical coherence tomography". Biomedical Optics Express. 5 (9): 3192–203. doi:10.1364/BOE.5.003192. PMC 4230859. PMID 25401031.
- ↑ Berg, S. A.; Eldik, S.; Bhattacharya, N. (2015). "Mode-resolved frequency comb interferometry for high-accuracy long distance measurement". Scientific Reports. 5: 14661. Bibcode:2015NatSR...514661V. doi:10.1038/srep14661. PMC 4588503. PMID 26419282.
- ↑ Chen, X; Gao, Y; Jiang, J; Liu, M; Luo, A; Luo, Z; Xu, W (2020). "High-repetition-rate pulsed fiber laser based on virtually imaged phased array". Chinese Optics Letters. 18 (7): 071403. doi:10.3788/COL202018.071403.
- ↑ Li, Z; Zang, Z; Han, Y; Wu, L; Fu, H (2021). "Solid-state FMCW LiDAR with two-dimensional spectral scanning using a virtually imaged phased array". Optics Express. 29 (11): 16547–16562. doi:10.1364/OE.418003.
- ↑ Zou, W; Peng, C; Liu, A; Zhu, R; Ma, J; Gao, L (2022). "Ultrafast two-dimensional imaging for surface defects measurement of mirrors based on a virtually imaged phased-array". Optics Express. 30 (21): 37235–37244. doi:10.1364/OE.469315.
- ↑ Metz, P.; Block, H.; Behnke, C.; Krantz, M.; Gerken, M.; Adam, J. (2013). "Tunable elastomer-based virtually imaged phased array". Optics Express. 21 (3): 3324–35. Bibcode:2013OExpr..21.3324M. doi:10.1364/OE.21.003324. PMID 23481792.
- ↑ Shirasaki, M.; Akhter, A. N.; Lin, C. (1999). "Virtually imaged phased array with graded reflectivity". IEEE Photonics Technology Letters. 11 (11): 1443. Bibcode:1999IPTL...11.1443S. doi:10.1109/68.803073. S2CID 8915803.
- ↑ Vega, A.; Weiner, A. M.; Lin, C. (2003). "Generalized grating equation for virtually-imaged phased-array spectral dispersers". Applied Optics. 42 (20): 4152–5. Bibcode:2003ApOpt..42.4152V. doi:10.1364/AO.42.004152. PMID 12856727.
- ↑ Xiao, S.; Weiner, A. M.; Lin, C. (2004). "A dispersion law for virtually imaged phased-array spectral dispersers based on paraxial wave theory". IEEE Journal of Quantum Electronics. 40 (4): 420. Bibcode:2004IJQE...40..420X. doi:10.1109/JQE.2004.825210. S2CID 1352376.