| Walther graph | |
|---|---|
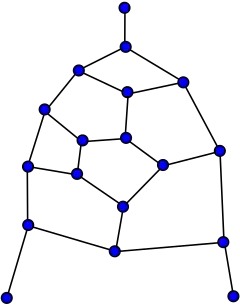 Walther graph | |
| Named after | Hansjoachim Walther |
| Vertices | 25 |
| Edges | 31 |
| Radius | 5 |
| Diameter | 8 |
| Girth | 3 |
| Automorphisms | 1 |
| Chromatic number | 2 |
| Chromatic index | 3 |
| Properties | Bipartite Planar |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Walther graph, also called the Tutte fragment, is a planar bipartite graph with 25 vertices and 31 edges named after Hansjoachim Walther.[1] It has chromatic index 3, girth 3 and diameter 8.
If the single vertex of degree 1 whose neighbour has degree 3 is removed, the resulting graph has no Hamiltonian path. This property was used by Tutte when combining three Walther graphs to produce the Tutte graph,[2] the first known counterexample to Tait's conjecture that every 3-regular polyhedron has a Hamiltonian cycle.[3]
Algebraic properties
The Walther graph is an identity graph; its automorphism group is the trivial group.
The characteristic polynomial of the Walther graph is :
References
- ↑ Weisstein, Eric W. "Walther Graph". MathWorld.
- ↑ Tutte, W. T. (1946), "On Hamiltonian circuits" (PDF), Journal of the London Mathematical Society, 21 (2): 98–101, doi:10.1112/jlms/s1-21.2.98
- ↑ Tait, P. G. (1884), "Listing's Topologie", Philosophical Magazine, 5th Series, 17: 30–46. Reprinted in Scientific Papers, Vol. II, pp. 85–98.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.