In graph theory, the Weisfeiler Leman graph isomorphism test is a heuristic test for the existence of an isomorphism between two graphs G and H.[1] It is based on a normal form for graphs first described in an article by Weisfeiler and Leman in 1968.[2] There are several versions of the test, these versions are referred to in the literature by various names, which easily leads to confusion.
The basic Weisfeiler Leman graph isomorphism test
The basic version called WLtest takes a graph as input, produces a partition of the nodes which is invariant under automorphisms and outputs a string certificate encoding the partition. When applied to two graphs G and H we can compare the certificates. If the certificates do not agree the test fails and G and H cannot be isomorphic. If the certificates agree, G and H may or may not be isomorphic.
The partition is produced in several rounds starting from the trivial partition where all nodes belong to the same component. In each round the partition is refined, which means that once two nodes are in different components they will also be in different components at future rounds. The partition refinement stops when the partition from the last round and the current partition are the same. This means that the refinement stops after rounds where n is the number of nodes in the graph. This is because the number of components need to grow by at least 1 in each step and the number of components cannot exceed n.
Membership of a node in a component is indicated by a label. In each round labels are recomputed and refined. After termination of the refinement, stringing together the labels after sorting yields the certificate. In order for isomorphic graphs to produce the same certificate one has to be very cautious with the labels because an isomorphism may swap nodes and may modify the order in which nodes are processed which in turn may alter the certificate. As an example the labels in the end may be 2-fold x, a single y and 2-fold z for one graph and a 2-fold x, 2-fold y and single z for an isomorphic graph yielding after sorting and stringing x_x_y_z_z resp. x_x_y_y_z.
One can be less careful with the labels, if one applies WLtest to a single graph created as the disjoint union of the two graphs G and H. Applying to the disjoint union will ensure that both graphs are processed in parallel at each stage, which will avoid such a swap of labels, say x and y as in the example above. Additionally the parallel processing can distinguish even more pairs of non-isomorphic graphs, see the examples below. In what follows we will discuss this version WLpairs.
The refinement of the partition in each step is by processing for each node its label and the labels of its nearest neighbors. Therefore WLtest can be viewed as a message passing algorithm.
Code
# ALGORITHM WLpairs
# INPUT: two graphs G and H to be tested for isomorphism
# OUTPUT: Certificates for G and H and whether they agree
U = combineTwo(G, H)
glabels = initializeLabels(U) # dictionary where every node gets the same label 0
labels = {} # dictionary that will provide translation from a string of labels of a node and its neighbors to an integer
newLabel = 1
done = False
while not(done):
glabelsNew = {} # set up the dictionary of labels for the next step
for node in U:
label = str(glabels[node]) + str([glabels[x] for x in neighbors of node].sort())
if not(label in labels): # a combination of labels from the node and its neighbors is encountered for the first time
labels[label] = newLabel # assign the string of labels to a new number as an abbreviated label
newLabel += 1 # increase the counter for assigning new abbreviated labels
glabelsNew[node] = labels[label]
if (number of different labels in glabels) == (number of different labels in glabelsNew):
done = True
else:
glabels = glabelsNew.copy()
certificateG = certificate for G from the sorted labels of the G-part of U
certificateH = certificate for H from the sorted labels of the H-part of U
if certificateG == certificateH:
test = True
else:
test = False
Here is some actual Python code which includes the description of the first examples.
g5_00 = {0: {1, 2, 4}, 1: {0, 2}, 2: {0, 1, 3}, 3: {2, 4}, 4: {0, 3}}
g5_01 = {0: {3, 4}, 1: {2, 3, 4}, 2: {1, 3}, 3: {0, 1, 2}, 4: {0, 1}}
g5_02 = {0: {1, 2, 4}, 1: {0, 3}, 2: {0, 3}, 3: {1, 2, 4}, 4: {0, 3}}
def combineTwo(g1, g2):
g = {}
n = len(g1)
for node in g1:
s = set()
for neighbor in g1[node]:
s.add(neighbor)
g[node] = s.copy()
for node in g2:
s = set()
for neighbor in g2[node]:
s.add(neighbor + n)
g[node + n] = s.copy()
return g
g = combineTwo(g5_00, g5_02)
labels = {}
glabels = {}
for i in range(len(g)):
glabels[i] = 0
glabelsCount = 1
newlabel = 1
done = False
while not (done):
glabelsNew = {}
glabelsCountNew = 0
for node in g:
label = str(glabels[node])
s2 = []
for neighbor in g[node]:
s2.append(glabels[neighbor])
s2.sort()
for i in range(len(s2)):
label += "_" + str(s2[i])
if not (label in labels):
labels[label] = newlabel
newlabel += 1
glabelsCountNew += 1
glabelsNew[node] = labels[label]
if glabelsCount == glabelsCountNew:
done = True
else:
glabelsCount = glabelsCountNew
glabels = glabelsNew.copy()
print(glabels)
g0labels = []
for i in range(len(g0)):
g0labels.append(glabels[i])
g0labels.sort()
certificate0 = ""
for i in range(len(g0)):
certificate0 += str(g0labels[i]) + "_"
g1labels = []
for i in range(len(g1)):
g1labels.append(glabels[i + len(g0)])
g1labels.sort()
certificate1 = ""
for i in range(len(g1)):
certificate1 += str(g1labels[i]) + "_"
if certificate0 == certificate1:
test = True
else:
test = False
print("Certificate 0:", certificate0)
print("Certificate 1:", certificate1)
print("Test yields:", test)
Examples
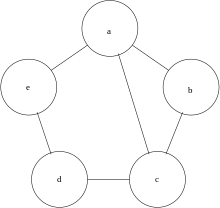
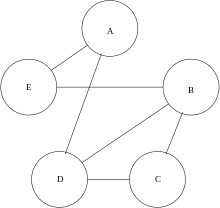
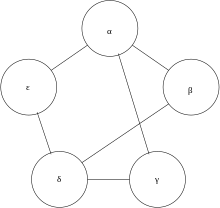
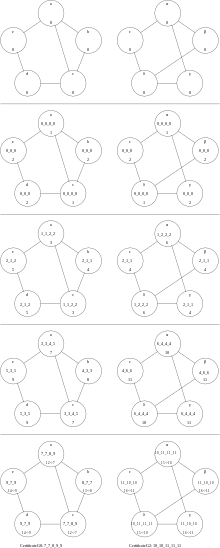
The first three examples are for graphs of order 5.[3]
| Graph G0 | Graph G1 | Graph G2 |
|---|---|---|
|
|
|
|
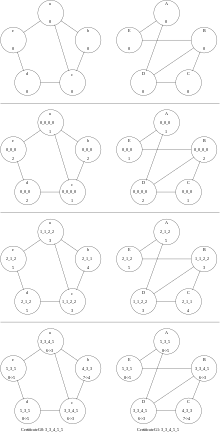
WLpair takes 3 rounds on 'G0' and 'G1'. The test succeeds as the certificates agree.
WLpair takes 4 rounds on 'G0' and 'G2'. The test fails as the certificates disagree. Indeed 'G0' has a cycle of length 5, while 'G2' doesn't, thus 'G0' and 'G2' cannot be isomorphic.
WLpair takes 4 rounds on 'G1' and 'G2'. The test fails as the certificates disagree. From the previous two instances we already know .
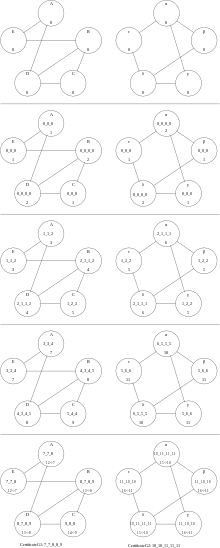
| G0 vs. G1 | G0 vs. G2 | G1 vs. G2 |
|---|---|---|
|
|
|
|
Indeed G0 and G1 are isomorphic. Any isomorphism must respect the components and therefore the labels. This can be used for kernelization of the graph isomorphism problem. Note that not every map of vertices that respects the labels gives an isomorphism. Let and be maps given by resp. . While is not an isomorphism constitutes an isomorphism.
When applying WLpair to G0 and G2 we get for G0 the certificate 7_7_8_9_9. But the isomorphic G1 gets the certificate 7_7_8_8_9 when applying WLpair to G1 and G2. This illustrates the phenomenon about labels depending on the execution order of the WLtest on the nodes. Either one finds another relabeling method that keeps uniqueness of labels, which becomes rather technical, or one skips the relabeling altogether and keeps the label strings, which blows up the length of the certificate significantly, or one applies WLtest to the union of the two tested graphs, as we did in the variant WLpair. Note that although G1 and G2 can get distinct certificates when WLtest is executed on them separately, they do get the same certificate by WLpair.
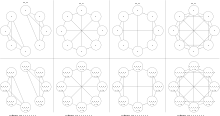
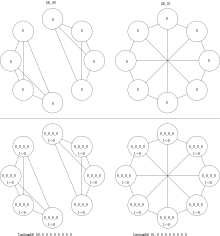
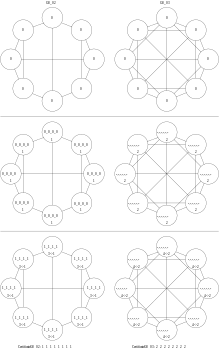
The next example is about regular graphs. WLtest cannot distinguish regular graphs of equal order,[4]: 31 but WLpair can destinguish regular graphs of distinct degree even if they have the same order. In fact WLtest terminates after a single round as seen in these examples of order 8, which are all 3-regular except the last one which is 5-regular.
All four graphs are pairwise non-isomorphic. G8_00 has two connected components, while the others do not. G8_03 is 5-regular, while the others are 3-regular. G8_01 has no 3-cycle while G8_02 does have 3-cycles.
| WLtest applied to four regular graphs of order 8. | WLpair applied to G8_00 and G8_01 of same degree. | WLpair applied to G8_02 and G8_03 of distinct degree. |
|---|---|---|
|
|
|
|
Another example example of two non-isomorphic graphs that WLpair cannot distinguish is given here.[5]
Applications
The theory behind the Weisfeiler Leman test is applied in graph neural networks.
Weisfeiler Leman graph kernels
In machine learning of nonlinear data one uses kernels to represent the data in a high dimensional feature space after which linear techniques such as support vector machines can be applied. Data represented as graphs often behave nonlinear. Graph kernels are method to preprocess such graph based nonlinear data to simplify subsequent learning methods. Such graph kernels can be constructed by partially executing a Weisfeiler Leman test and processing the partition that has been constructed up to that point.[6] These Weisfeiler Leman graph kernels have attracted considerable research in the decade after their publication.[1] They are also implemented in dedicated libraries for graph kernels such as GraKeL.[7]
Note that kernels for artificial neural network in the context of machine learning such as graph kernels are not to be confused with kernels applied in heuristic algorithms to reduce the computational cost for solving problems of high complexity such as instances of NP-hard problems in the field of complexity theory. As stated above the Weisfeiler Leman test can also be applied in the later context.
See also
References
- 1 2 Huang, Ningyuan; Villar, Soledad (2022), "A Short Tutorial on the Weisfeiler-Lehman Test and Its Variants", ICASSP 2021 - 2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 8533–8537, arXiv:2201.07083, doi:10.1109/ICASSP39728.2021.9413523, ISBN 978-1-7281-7605-5, S2CID 235780517
- ↑ Weisfeiler, B. Yu.; Leman, A. A. (1968). "A Reduction of a Graph to a Canonical Form and an Algebra Arising during This Reduction" (PDF). Nauchno-Technicheskaya Informatsia. 2 (9): 12–16. Retrieved 2023-10-28.
- ↑ Bieber, David (2019-05-10). "The Weisfeiler-Lehman Isomorphism Test". Retrieved 2023-10-28.
- ↑ Kiefer, Sandra (2020). Power and limits of the Weisfeiler-Leman algorithm (PhD thesis). RWTH Aachen University. Retrieved 2023-10-29.
- ↑ Bronstein, Michael (2020-12-01). "Expressive Power Of Graph Neural Networks And The Weisfeiler-Lehman Test". Retrieved 2023-10-28.
- ↑ Shervashidze, Nino; Schweitzer, Pascal; Van Leeuwen, Erik Jan; Mehlhorn, Kurt; Borgwardt, Karsten M. (2011). "Weisfeiler-lehman graph kernels". Journal of Machine Learning Research. 12 (9): 2539−2561. Retrieved 2023-10-29.
- ↑ "Weisfeiler Lehman Framework". 2019. Retrieved 2023-10-29.
This Weisfeiler Lehman framework operates on top of existing graph kernels and is inspired by the Weisfeiler-Lehman test of graph isomorphism [WL68].