William Chapple (1718–1781) was an English surveyor and mathematician. His mathematical discoveries were mostly in plane geometry and include:

He was also one of the earliest mathematicians to calculate the values of annuities.

Life

Chapple was born in Witheridge on 25 January 1719 [O.S. 14 January 1718], the son of a poor farmer and parish clerk.[1] He was a devoted bibliophile,[2] and gained much of his knowledge of mathematics from Ward's The Young Mathematician's Guide: Being a Plain and Easie Introduction to the Mathematicks, in Five Parts.[3] He became an assistant to the parish priest, and a regular contributor to The Ladies' Diary, especially concerning mathematical problems. He also later contributed work on West Country English to The Gentleman's Magazine.[1]

His correspondence led him to become, in 1738, the clerk for a surveyor in Exeter. He married the surveyor's niece, supervised the construction of a new hospital in Exeter, and became secretary of the hospital.[1] He also worked as the estate steward for William Courtenay, 1st Viscount Courtenay.[4] In 1772 he began work on an update to Tristram Risdon's Survey of the County of Devon, and spent much of the rest of his life working on it; it was published in part throughout his life, and in complete form posthumously in 1785.[1]

He died in early September 1781.[1] A tablet in his memory could be found in the west end of the nave of the Church of St Mary Major, Exeter, prior to that church's demolition in 1971.[5] Chapple Road in Witheridge is named after him.[2]

Contributions to mathematics

Andrea del Centina writes that:

"To illustrate the work of Chapple, whose arguments are often confused and whose logic is very poor, even for the standard of his time, is not easy especially when trying to keep as faithful as possible to his thought."[3]

Nevertheless, Chapple made several significant discoveries in mathematics.

Plane geometry

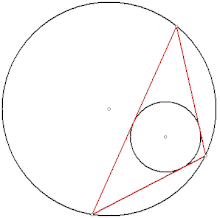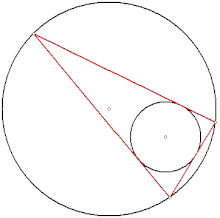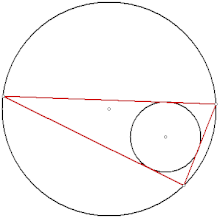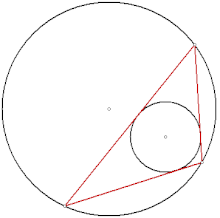
The triangular case of Poncelet's closure theorem

Euler's theorem in geometry gives a formula for the distance between the incentre and circumcentre of a circle, as a function of the inradius and circumradius :

An immediate consequence is the related inequality . Although these results are named for Leonhard Euler, who published them in 1765, they were found earlier by Chapple, in a 1746 essay in The Gentleman's Magazine.[6][7] In the same work he stated that, when two circles are the incircle and circumcircle of a triangle, then there is an infinite family of triangles for which they are the incircle and circumcircle. This is the triangular case of Poncelet's closure theorem, which applies more generally to polygons of any number of sides and to conics other than circles. It is the first known mathematical publication on pairs of inscribed and circumscribed circles of polygons, and significantly predates Poncelet's own 1822 work in this area.[3]

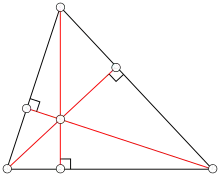
Three altitudes of a triangle meet at the orthocentre

In 1749, Chapple published the first known proof of the existence of the orthocentre of a triangle, the point where the three perpendiculars from the vertices to the sides meet. The orthocentre itself was known previously, but Chapple writes that its existence was "often taken for granted, but no where demonstrated".[8]

Finance

Chapple learned of the problem of valuation of annuities through his correspondence with John Rowe and Thomas Simpson, and carried out this valuation for Courtenay. In this, he became one of the first mathematicians to work on this problem, along with Simpson, Abraham de Moivre, James Dodson, and William Jones.[4]

References

  1. 1 2 3 4 5 Pengelly, W. (1887), "Prince's "Worthies of Devon" and the "Dictionary of National Biography", part III", Report & Transactions of the Devonshire Association, Devonshire Association for the Advancement of Science Literature & the Arts, 19: 217–348. See in particular "Chapple, William", pp. 316–318.
  2. 1 2 "William Chapple", Witheridge Historical Archive, retrieved 18 November 2019
  3. 1 2 3 Del Centina, Andrea (2016), "Poncelet's porism: a long story of renewed discoveries, I", Archive for History of Exact Sciences, 70 (1): 1–122, doi:10.1007/s00407-015-0163-y, MR 3437893, S2CID 253898210
  4. 1 2 Bellhouse, David R. (2017), Leases for Lives: Life Contingent Contracts and the Emergence of Actuarial Science in Eighteenth-Century England, Cambridge University Press, p. 79, ISBN 9781108509121
  5. ↑ Lysons, Daniel (1822), Magna Brittanica; being a concise topographical account of the several counties of Great Britain, Vol. VI: Devonshire, Thomas Cadell, p. 215
  6. ↑ Milne, Antony (2015), "The Euler and Grace-Danielsson inequalities for nested triangles and tetrahedra: a derivation and generalisation using quantum information theory", Journal of Geometry, 106 (3): 455–463, arXiv:1404.0525, doi:10.1007/s00022-014-0257-8, MR 3420559
  7. ↑ Chapple, William (1749), "An essay on the properties of triangles inscribed in, and circumscribed about two given circles", Miscellanea Curiosa Mathematica, The Gentleman's Magazine, vol. 4, pp. 117–124
  8. ↑ Bogomolny, Alexander, "A Possibly First Proof of the Concurrence of Altitudes", Cut The Knot, retrieved 17 November 2019. See also Chapple's letter with the proof.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.