XPIC, or cross-polarization interference cancelling technology, is an algorithm to suppress mutual interference between two received streams in a Polarization-division multiplexing communication system.

The cross-polarization interference canceller (known as XPIC) is a signal processing technique implemented on the demodulated received signals at the baseband level. It is typically necessary in Polarization Division Multiplexing systems: the data sources to be transmitted are coded and mapped into QAM modulating symbols at the system's symbol rate and upconverted to a carrier frequency, generating two radio streams radiated by a single dual-polarized antenna (see feed pattern of Parabolic antenna). A corresponding dual-polarized antenna is located at the remote site and connected to two receivers, which downconvert the radio streams into baseband signals (BB H, BB V).

This multiplexing/demultiplexing technique is based on the expected discrimination between the two orthogonal polarizations (XPD):

• an ideal, infinite XPD of the whole system guarantees that each signal at the receivers contains only the signal generated by the corresponding transmitter (plus any thermal noise);
• any real, finite, level of XPD instead manifests itself as a partial recombination between the two signals, so that the receivers observe an interference due to the cross-polarization leakage. Some of the factors causing such cross-polarization interference are listed in Polarization-Division Multiplexing.

Polarization-Division Communication System

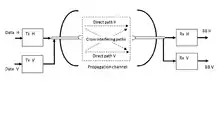
As a practical consequence, at the receiving site the two streams are received with a residual mutual interference. In many practical cases, especially for high-level M-QAM modulations, the communication system cannot tolerate the experienced levels of cross-polarization interference and an improved suppression is necessary. The two received polarizations at the antenna outputs, normally linear horizontal H and vertical V, are routed each to a receiver whose baseband output is further processed by an ad-hoc cross-polarization cancelling scheme, commonly implemented as a digital stage. The XPIC algorithm attains the correct reconstruction of H by summing V to H to cancel any residual interference, and vice versa.

Cross-polarization cancelling scheme involving equalization on the main path, XPIC filtering on the cross-polarized component and decision (slicing) with computation of residual error

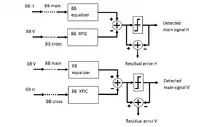
The cancelling process is typically implemented using two blocks: a baseband equalizer and the baseband XPIC. The output from the latter is subtracted from the former and then sent to the decision stage, responsible for yielding the estimation of the data stream. The equalization and XPIC blocks are normally adaptive for a correct tracking of the time-variant channel transfer function: XPIC must provide a shaping of the received cross signal equal to the portion of the cross interference affecting the main one. The feedback control to drive the adapting criteria comes from the measure of the residual error across the decision block.

Equalization and XPIC filtering stages; the output of the latter is subtracted from the former before decision and computation of decision error

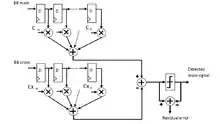
In the example, both blocks are based on the typical structure of the Finite Impulse Response digital filter and whose the coefficients are not fixed, but adapted to minimize a suitable functional ${\displaystyle J}$ while multiple delays ${\displaystyle D}$ act on the input signal.

Given:

• ${\displaystyle \epsilon _{k}}$: residual complex error at time instant ${\displaystyle k}$,
• ${\displaystyle s_{k}^{(m)}}$: baseband main received signal complex sample at time instant ${\displaystyle k}$,
• ${\displaystyle s_{k}^{(x)}}$: baseband cross received signal complex sample at time instant ${\displaystyle k}$,
• ${\displaystyle C_{j,k}^{(m)}}$: complex coefficient of baseband equalizer on the tap j and time instant ${\displaystyle k}$,
• ${\displaystyle C_{j,k}^{(x)}}$: XPIC complex coefficient on tap j and time instant ${\displaystyle k}$,
• ${\displaystyle j=-n,...,n}$: index of tap
• ${\displaystyle y_{k}}$: result of cancelling action feeding the decision device at time instant ${\displaystyle k}$,
• ${\displaystyle d_{k}}$: estimated transmitted data at time instant ${\displaystyle k}$, so ${\displaystyle \epsilon _{k}}$ = ${\displaystyle y_{k}}$ - ${\displaystyle d_{k}}$
• ${\displaystyle \gamma }$: step-size or compression factor for adaptativity,

if the function to minimize is for example the mean power the residual error, ${\displaystyle J=E[|\epsilon _{k}|^{2}]}$, the adapting gradient algorithm prescribes that the coefficients are updated after every time step ${\displaystyle k}$ as:^[1]

• ${\displaystyle C_{j,k+1}^{(m)}=C_{j,k}^{(m)}-\gamma \epsilon _{k}(s_{k-j}^{(m)})^{*}}$;
• ${\displaystyle C_{j,k+1}^{(x)}=C_{j,k}^{(x)}-\gamma \epsilon _{k}(s_{k-j}^{(x)})^{*}}$;

where the asterisk denotes complex-conjugation. No a-priori knowledge on the transmitted symbols is required with this basic scheme (blind or zero-knowledge).

When the delay ${\displaystyle D}$ is equal to the symbol period, the blocks are denoted as symbol-spaced, while if ${\displaystyle D}$ is a fraction of the symbol period the blocks are said to be fractionally-spaced.^[2] Other minimizing functions are least mean square LMS or zero forcing ZF while the architecture can be a Decision Feedback or further improved by means of known signals (Pilot signal).

See also

• Interference erasing system with independent receivers patent
• Cross-polarization transmission system with asynchronous receivers patent
• Communications system
• Adaptive equalizer

References