Z-HIT, also denoted as ZHIT, Z-HIT-Algorithmn or Z-HIT-Approximation, is a bidirectional mathematical relation, connecting the two parts of any complex function, - i.e. real and imaginary part. Concerning practical impedance measurements and in contrast to the Kramers–Kronig relations, where the real part can be computed from the imaginary part (or vice versa), in the Z-HIT the impedance modulus is computed by the course of the phase angle. In addition, the angular frequency (ω) boundaries for computing one component of the complex function from the other one using the Kramers-Kronig relations, are ω=0 and ω=∞; these boundaries require extrapolation procedures of the measured impedance spectra. Concerning the ZHIT however, the computing of the course of the impedance modulus from the course of the phase shift can be performed within the measured frequency range, without the need of extrapolation. This avoids complications which may arise from the fact that impedance spectra can only be measured in a limited frequency range. Therefore, the Z-HIT-algorithm allows for verification of the stationarity of the measured test object as well as calculating the impedance values using the phase data. The latter property becomes important when drift effects are present in the impedance spectra which had to be detected or even removed when analysing and/or interpreting the spectra.
Motivation
An important application of Z-HIT is the examination of experimental impedance spectra for artifacts. The examination of EIS series measurements is often difficult due to the tendency of examined objects to undergo changes during the measurement. This may occur in many standard EIS applications such as the evaluation of fuel cells or batteries during discharge. Further examples include the investigation of light-sensitive systems under illumination (e.g. Photoelectrochemistry) or the analysis of water uptake of lacquers on metal surfaces (e.g. corrosion-protection). A descriptive example for an unsteady system is a Lithium-ion battery. Under cyclization or discharging, the amount of charge in the battery changes over time. The change in charge is coupled with a chemical redox reaction, transferring to a change in concentrations of the involved substances. This violates the principles of stationarity and causality which are prerequisites for proper EIS measurements. In theory, this would exclude drift-affected samples from valid evaluation. Using the ZHIT-algorithm, these and similar artifacts can be recognized and spectra following causality can even be reconstructed, which are consistent with the Kramers–Kronig relations and thereby valid for analysis.
Mathematical Formulation
Z-HIT is a special case of the Hilbert transform and through restriction by the Kramers–Kronig relations it can be derived for one-Port-systems. The frequency-dependent relationship between impedance and phase angle can be observed in the Bode plot of an impedance spectrum. Equation (1) is obtained as a general solution of the correlation between impedance modulus and phase shift.[1][2]
Equation (1) indicates that the logarithm of the impedance () at a specific frequency can be calculated up to a constant value of (), if the phase shift is integrated up to the frequency point of interest , while the starting value of the integral can be freely chosen. As an additional contribution to the calculation of , the odd-numbered derivatives of the phase shift at the point have to be added, weighted with the factors . The factors can be calculated according to equation (2), whereat represents the Riemann ζ-function.
| 2 | ||
| 4 | ||
| 6 | ||
| 8 |
The practically applied Z-HIT approximation is obtained from equation (1) by limitation to the first derivative of the phase shift neglecting higher derivatives (equation (3)), where C represents a constant.
The free choice of the integration boundaries in the ZHIT algorithm is a fundamental difference concerning the Kramers-Kronig relations; in ZHIT the integration boundaries are and . The greatest advantage of the ZHIT results from the fact, that both integration boundaries can be chosen within the measured spectrum, and thus does not require extrapolation to frequencies 0 and , as with the Kramers-Kronig relations.
Practical implementation
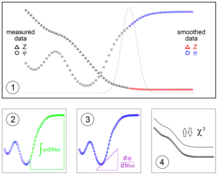
The practical implementation of the Z-HIT approximation is shown schematically in Figure 1. A continuous curve (spline) for each of the two independent measured quantities (impedance and phase) is created by smoothing (part 1 in Figure (1)) from the measured data points. With the help of the spline for the phase shift, values for the impedance are now calculated. First, the integral of the phase shift is calculated up to the corresponding frequency , where (if suited) the highest measured frequency is selected as starting point for the integration - c.f. part 2 in Figure (1). From the spline of the phase shift, its slope can be calculated at (part 3 in figure (1)). Thereby, a reconstructed curve of the impedance is obtained which is (in the ideal case) only shifted parallelly with regard to the measured curve. There exist several possibilities to determine the constant C in the Z-HIT equation (part 4 in Figure (1)), one of which contains a parallel shift of the reconstructed impedance in a frequency range not affected by artifacts (see notes). This shift is performed by a linear regression procedure. Comparing the resulting reconstructed impedance curve to the measured data (or the Splines of the impedance), artifacts can easily be detected. These are usually located in the high frequency range (caused by induction or mutual induction, especially when low impedance systems are investigated) or in the low frequency range (caused by the change of the system during the measurement (=drift)).
Notes (time requirements during measurement)
The measurement time required for a single impedance measurement point strongly depends on the frequency of interest. While frequencies above about 1 Hz can be measured within seconds, the measurement time increases significantly in the lower frequency range. Although the exact duration for measuring a complete impedance spectrum depends on the measauring device as well as on internal settings, the following measurement times can be considered as rules of thumb when measuring the frequency measurement points sequentially, with the upper frequency assumed as 100 kHz or 1 MHz:
- Down to approx. 1 Hz, the measuring time is approx. 1 minute
- Down to 0.1 Hz approx. 5 minutes
- Down to 0.05 Hz approx. 10 minutes
- Down to 0.02 Hz approx. 15 minutes
- Down to 0.01 Hz approx. 30 minutes
Measurements down to or below 0.01 Hz are typically associated with measurement times in the range of several hours. Therefore, a spectrum can be roughly divided into three sub-ranges with regard to the occurrence of artifacts: in the high-frequency domain (approx. > 100 to 1000 Hz), induction or mutual induction can dominate. In the low frequency region (< 1 Hz), drift can occur due to noticeable change in the system. The range between about 1 Hz and 1000 Hz is usually not affected by high- or low-frequency artifacts. However, the mains frequency (50/60 Hz) may come into play as distorting artifact in this region.
Notes (application procedure)
In addition to the reconstruction of the impedance from the phase shift, the reverse approach is also possible.[2] However, the herein presented procedure possesses several advantages:
- When calculating the phase shift from the impedance, a function of the angular frequency ω comes into play which is more difficult to determine compared to the constant C in equation (3).
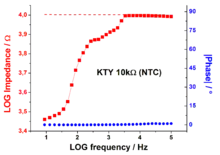 Figure 2: Impedance measurement of a temperature sensor KTY (10 KΩ), where heating of the sensor was started during the measurement.
Figure 2: Impedance measurement of a temperature sensor KTY (10 KΩ), where heating of the sensor was started during the measurement. - Generally, the phase shift is more stable than the impedance. This is based on the fact that for impedance elements (more precisely: Constant phase element, CPE[4][5] ) the property "phase shift" remains constant even if the value of the impedance drastically changes. Such Constant Phase-elements are the typical electronic elements, among others such as the electrical resistor, capacitor and coil. For illustration, Figure 2 shows the impedance spectrum of an NTC resistor heated during the measurement (starting between 1 kHz and 10 kHz down to lower frequencies). It can clearly be seen that the value of the impedance (red curve) changes with temperature, while the phase shift (blue curve) remains constant. In other words, "a resistor remains a resistor".
- The reconstruction of the impedance from the phase shift further restores the "inner (= complex)" relationship between these two quantities. This relationship is lost by the independent construction of the supporting point splines for impedance and phase (Figure 1). Depending on the system under investigation, this restored correlation - even in the absence of artifacts - can lead to an improved evaluation of the spectra. In such cases, the gain in accuracy due to the reconstruction of the complex impedance outweighs the approximation error according to equation (3), which results from the neglection of the higher derivatives.
Applications
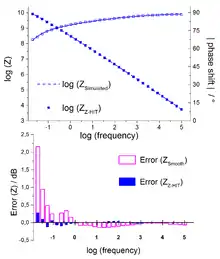
Figure 3 shows an impedance spectrum of a measurement series of a painted steel sample during water uptake [6] (upper part in Figure 3). The symbols in the diagram represent the interpolation points (nodes) of the measurement, while the solid lines represent the theoretical values simulated according to an appropriate model. The interpolation points for the impedance were obtained by the Z-HIT reconstruction of the phase shift. The bottom part of Figure 3 depicts the normalized error (ZZHIT − Zsmooth)/ZZHIT·100 of the impedance. For the error calculation, two different procedures are used to determine the "extrapolated impedance values":
- the "extrapolated impedance values" can be calculated from the "splined (=Zsmooth)" data of the impedance (magenta)
- the impedance values (blue) can be reconstructed by the Z-HIT (= ZZ-HIT) using the spline of the phase shift
The simulation according to the appropriate model is performed using the two different impedance curves. The corresponding residuals are calculated and depicted in the bottom part of the diagram in Figure (3). Note: Error patterns as shown in the magenta bottom diagram in Figure (3) may be the motivation to extend an existing model by additional elements to minimize the fitting error. However, this is not possible in every case. The drift in the impedance spectrum mainly influences the low-frequency part by means of a changing system during the measurement. The spectrum in Figure 3 is caused by water penetrating into the pores of the lacquer, which reduces the impedance (resistance) of the coating. Therefore, the system behaves as if at each low-frequency measurement point the resistance of the coating was replaced by a further, smaller resistance due to the water uptake. However, there is no impedance element that exhibits such behavior. Therefore, any extension of the model would only result in a "smearing" of the error over a wider frequency range without reducing the error itself. Only the removal of the drift by reconstructing the impedance using Z-HIT leads to a significantly better compatibility between measurement and model.
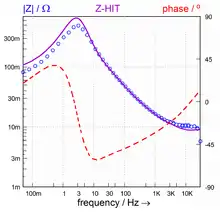
Figure 4 shows a Bode plot of an impedance series measurement, performed on a fuel cell where the hydrogen of the fuel gas was deliberately poisoned by the addition of carbon monoxide.[7] Due to the poisoning, active centers of the platinum catalyst are blocked, which severely impairs the performance of the fuel cell. Thereby, the blocking of the catalyst is depending on the potential, resulting in an alternating sorption and desorption of the carbon monoxide on the catalyst surface within the cell. This cyclical change of the active catalyst surface translates to pseudo-inductive behavior, which can be observed in the impedance spectrum of Figure 4 at low frequencies (< 3 Hz). The impedance curve was reconstructed by Z-HIT and is represented by the purple line, while the originally measured values are represented by the blue circles. The deviation in the low frequency part of the measurement can be clearly observed. Evaluation of the spectra shows [7] significantly better agreement between model and measurement if the reconstructed Z-HIT impedances are used instead of the original data.
References
Original work:
- C. A. Schiller; F. Richter; E. Gülzow; N. Wagner (2001), "Validation and evaluation of electrochemical impedance spectra of systems with states that change with time", Physical Chemistry Chemical Physics (in German), vol. 3, no. 3, pp. 374–378, doi:10.1039/B007678N
- W. Ehm, R. Kaus, C. A. Schiller, W. Strunz: Z-HIT — A Simple Relation Between Impedance Modulus and Phase Angle. Providing a New Way to the Validation of Electrochemical Impedance Spectra. In: F. Mansfeld, F. Huet, O. R. Mattos (Hrsg.): New Trends in Electrochemical Impedance Spectroscopy and Electrochemical Noise Analysis. Electrochemical Society Inc., Pennington, NJ, 2001, vol. 2000-24, ISBN 1-56677-291-5, S. 1–10.
- Andrzej Lasia: Z-HIT Transform. In:Electrochemical Impedance Spectroscopy and its Application. Springer New York Heidelberg Dordrecht London, 2014, ISBN 978-1-4614-8932-0, S. 299.
References
- ↑ W. Ehm; H. Gohr; R. Kaus; B. Roseler; C. A. Schiller (2000), "The evaluation of electrochemical impedance spectra using a modified logarithmic Hilbert transform", ACH-Models in Chemistry (in German), vol. 137, no. 2–3, pp. 145–157
- 1 2 W. Ehml (1998), Expansions for the Logarithmic Kramers—Kronig Relations (PDF auf www.zahner.de) (in German), retrieved 2014-11-29
- ↑ Numerical values of the Zetafunction
- ↑ CPE(mathematical)
- ↑ CPE(physical)
- ↑ W. Strunz; C. A. Schiller; J. Vogelsang (2008), "The change of dielectric properties of barrier coatings during the initial state of immersion", Materials and Corrosion (in German), vol. 59, no. 2, pp. 159–166, doi:10.1002/maco.200804156
- 1 2 C. A. Schiller; F. Richter; E. Gülzow; N. Wagner (2001), "Relaxation impedance as a model for the deactivation mechanism of fuel cells due to carbon monoxide poisoning", Physical Chemistry Chemical Physics (in German), vol. 3, no. 11, pp. 2113–2116, doi:10.1039/B007674K