亚历山大的希罗
亚历山大的希罗(希腊语:)(公元10年—70年) ,是一位古希腊数学家,居住于羅馬時期的埃及省。他也是一名活跃於其家鄉亚历山大的工程师,他被认为是古代最伟大的实验家[1],他的著作於希臘化時代科學傳統方面享負盛名。[2]
| 亚历山大的希罗 | |
|---|---|
 | |
| 出生 | 公元10年(在世時期) |
| 居住地 | 羅馬帝國時期的亚历山大 |
| 知名于 | 汽轉球 |
| 科学生涯 | |
| 研究领域 | 數學 |
海龍發明了一種叫汽轉球的蒸汽機。在他這麼多種發明之中,最著名的是風輪,這發明是其中一種最早利用風能的設備。一般認為他也是一位原子論者,他的一些思想乃源自克特西比烏斯(Ctesibius)的著作。
背景
由於希羅的作品深受巴比倫文化的影響,所以他曾被少數學者認為他是一位帶有埃及或腓尼基血統的希臘人。[3]但現代學者卻認為他是一位純希臘人。[4][1][5]數學歷史學家卡爾·本雅明·博耶(C. B. Boyer)解釋,希羅之所以被認為是埃及人或腓尼基人,是因為他的作品帶有濃烈的巴比倫色彩。但是最少自亚历山大大帝時期起至古典時代(Classical antiquity)結束的一段時期,希臘的確與美索不達米亞有許多來往,而且不難看到巴比倫的算術和代數幾何學一直對希臘化文明產生重大影響。[4]
事蹟
由於希羅大部份的作品(包括數學、力學、物理和氣體力學)都以講稿的形式出現,所以他被認為曾在繆斯之家教學(包括亞歷山大圖書館)。此外,雖然這些學術領域在二十世紀之前尚未正式化,但他的發明為模控學的研究資料。[6]希羅發明了許多設備,例如:汽轉球、自動售賣機、注射器、蒸氣風琴等。
發明
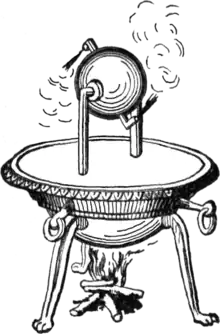
汽轉球
數學成就
希羅發明了一種用於反覆計算平方根的方法,[7] 叫做Babylonian method。這公式以Babylonian命名,是因為巴比倫人比希羅早知道這種計算法。現今人們比較熟悉希羅發明的海龍公式,這公式是以三角形的邊長來計算三角形的面積。
參考文獻
- Research Machines plc. . 亞平頓: Helicon Publishing. 2004年: 546.
Hero of Alexandria (lived c. AD 60) Greek mathematician and engineer, the greatest experimentalist of antiquity
- Marie Boas, "Hero's Pneumatica: A Study of Its Transmission and Influence", Isis, Vol. 40, No. 1 (Feb., 1949), p. 38 and supra
- George Sarton (1936年). "The Unity and Diversity of the Mediterranean World", Osiris 2, 第406至463頁 [第429頁] .
John H. Lienhard. . . 第1038集http://www.uh.edu/engines/epi1038.htm|transcripturl=缺少标题 (帮助). 1995年. NPR. KUHF-FM Houston.
T. D. De Marco (1974年). "Gas-Turbine Standby-Power Generation for Water-Treatment Plants", Journal American Water Works Association 66 (2), 第133至138頁.
Victor J. Katz (1998年). A History of Mathematics: An Introduction, 第184頁. Addison Wesley. ISBN 0-321-01618-1.
Justin E. Wilson (2006年). Heron’s Formula (页面存档备份,存于), University of North Carolina at Charlotte. - Boyer. . . 1968年 [1991年]: 第171至172頁.
At least from the days of Alexander the Great to the close of the classical world, there undoubtedly was much intercommunication between Greece and Mesopotamia, and it seems to be clear that the Babylonian arithmetic and algebraic geometry continued to exert considerable influence in the Hellenistic world. This aspect of mathematics, for example, appears so strongly in Heron of Alexandria (fl. ca. A.D. 100) that Heron once was thought to be Egyptian or Phoenician rather than Greek. Now it is thought that Heron portrays a type of mathematics that had long been present in Greece but does not find a representative among the great figures - except perhaps as betrayed by Ptolemy in the Tetrabiblos.
- Gregory A Tokaty. . Courier Dover Publications. 1994: 26. ISBN 0486681033.
Grolier Incorporated. . Grolier University of Michigan. 1989: 144. ISBN 0717220249.
Encyclopædia Britannica Online - Heron of Alexandria (页面存档备份,存于)
Israel Shatzman, Michael Avi-Yonah. . Harper and Row. 1975: 234. ISBN 0060101784.
Gillian Clements. . frances lincoln ltd. 2005: 13. ISBN 0711216053.
Enc. Britannica 2007, "Heron of Alexandria" - Kelly, Kevin. . Boston: Addison-Wesley. 1994年. ISBN 0-201-48340-8.
- Heath, Thomas. . 牛津: 牛津大学出版部印刷所. 1921年: 第323至324頁 [2009-07-06]. (原始内容存档于2013-06-07).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.