交叉數
在圖論,交叉數是將圖畫在平面上時,邊的交叉點的最小數目。若,則稱為平面圖。在圖形製圖方面,計算圖的交叉數仍是一個重要問題,因為讀者研究發現,畫圖的交叉越少,越有利於讀者理解。[1]
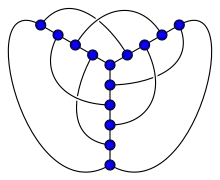
交叉數的研究始於圖蘭磚廠問題。圖蘭·帕爾想求磚廠中,將每個窯爐各與全部貨倉用路軌連接的最優方案,使路軌的交叉儘可能少。按上述定義,即是問完全二部圖的交叉數。[2]同一問題約莫同時在社會學研究提出,因為事關社會關係圖的繪製。[3] 圖蘭猜想了完全二部圖交叉數的公式,但該公式迄今未獲證,完全圖的交叉數公式亦然。
交叉數不等式斷言,若邊數与頂點數的比值大于某个常数,則交叉數不小于乘以另一个固定的常数。此結論在超大规模集成电路設計與組合幾何方面有應用。
如無特別註明,交叉數允許使用任意曲線來畫邊。另一個相關概念是直線交叉數,其要求僅使用直線段來畫邊,所以未必等於交叉數。更具體說,完全圖的直線交叉數就是平面上處於一般位置的個點所能組成的凸四邊形的最少數目,因為每個凸四邊形的兩條對角線產生一個交叉。直線交叉數問題與幸福結局問題密切相關。[4]
給定一個圖,計算其交叉數是一個NP難問題。[5]
定義
定義交叉數之前,先定義無向圖的畫法。圖的畫法是一個映射,其將圖的頂點映到平面上互異的點,並將每條邊映到一條連接其兩端的曲線段,但頂點不能映到其他邊上(除非該邊以其為頂點),且若兩條邊的曲線段在公共頂點以外相交,則其僅產生有限多個交叉,並於每個交叉處橫截相交。若一個交叉點有多於兩條邊相交,則每對相交邊計算一次。圖的交叉數是所有畫法當中,交叉的數目的最小值。[6]
一些作者對於畫法有更多限制,例如要求每對邊的交集至多只有一點(可為公共端點或交叉)。對於上段定義的交叉數,此項限制沒有任何影響,因為交叉最少的畫法當中,兩條邊必定相交至多一次。(若兩條邊有公共端點,而且相交,則可以將首個交點以前的兩段曲線互換,從而減少一個交叉。類似地,若兩條邊有兩個或更多交叉,則可以將相鄰兩個交叉之間的兩段曲線互換,以減少兩個交叉。)然而,若考慮交叉數的變式定義,例如只計算有多少對邊交叉(稱為兩兩交叉數),而非有多少個交叉,則上述限制確實會影響兩兩交叉數的值。[6]
特殊情況
截止2015年4月,僅得很少幾類圖的交叉數為人所知。即使是完全圖、完全二部圖、兩個環的積等結構較簡單的圖,也僅得初始幾個的交叉數是已知的,但交叉數的下界方面,已有一定進展。[7]
完全二部圖
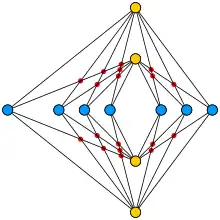
在第二次世界大戰期間,匈牙利數學家圖蘭·帕爾被迫在磚廠工作,要將一車車的磚從窯爐推到貨倉。工廠的每個窯爐到每個貨倉之間各有一條路軌,而磚車在路軌交叉處特別難推。於是,圖蘭提出其磚廠問題:窯爐、貨倉和路軌應如何安排,才能使交叉的數目最少?數學上,窯爐和貨倉可視為完全二部圖的頂點,而路軌則是二部圖的邊。於是工廠的佈局就是該圖在平面上的一個畫法,換言之問題變成: 完全二部圖的畫法中,交叉的最少數目是多少?[8]
卡齊米日·扎蘭凱維奇嘗試解決圖蘭磚廠問題,[9]但其證明有錯。不過,他成功推導出完全二部圖交叉數的一個上界:
一個猜想是,上述上界確實是所有完全二部圖的交叉數。[10]
完全圖與圖染色
完全圖的交叉數問題最先由安東尼·希爾提出,並於1960年出版。[11]希爾及其合作者約翰·恩斯特皆為對數學甚感興趣的構成主義藝術家。兩位不僅提出了問題,還猜想了該交叉數的公式,公式由理查·蓋於1960年出版。[11]具體來說,已知總有一種畫法,其交叉的數目為
上式在時,取值分別為,見整數數列線上大全的A000241號數列。希爾等人猜想,不存在更好的畫法,即上式給出了完全圖的交叉數。湯瑪士·沙提於1964年獨立地作出了同一個猜想。[12]
對於,沙提驗證了上式確實給出交叉的最小可能數目。潘(Shengjun Pan)和布魯斯·里希特(Bruce Richter)驗證了的情況。[13]
2007年,米高·艾伯森(Michael O. Albertson)提出了艾伯森猜想,其斷言:在所有色數為的圖之中,完全圖的交叉數最小。換言之,若此猜想與上段的猜想均成立,則每個染色數為的圖,交叉數皆不小於上段的公式。現已證明,艾伯森猜想對於成立。[14]
立方圖
已知交叉數為至的最小的立方圖,其頂點數分別為(OEIS數列A110507),如下表所記:
| 交叉數 | 最小立方圖例子 | 頂點數 |
|---|---|---|
| 1 | 完全二部圖 | 6 |
| 2 | 佩特森圖 | 10 |
| 3 | 希伍德圖 | 14 |
| 4 | 莫比烏斯-坎特圖 | 16 |
| 5 | 帕普斯圖 | 18 |
| 6 | 笛沙格圖 | 20 |
| 7 | 有4個不同構的例子,但並無熟知命名[15] | 22 |
| 8 | 瑙魯圖、麥基圖、(3,7)-籠圖[16] | 24 |
| 9 | 麥基圖加某一條邊[17] | 26 |
| 10 | 麥基圖加某兩條邊[17] | 28 |
| 11 | 考克斯特圖[18] | 28 |
2009年,愛德華·柏奇和Geoffrey Exoo猜想交叉數為13的最小立方圖為塔特-考克斯特圖,以及交叉數為170的最小立方圖為塔特12-籠。[16][19]
複雜度與近似
一般情況下,很難計算圖的交叉數。米高·加里和大衛·詹森於1983年證明了計算交叉數是NP難問題。[5]即使僅考慮立方圖[20],或者僅考慮將近平面的特殊情況(即可藉刪走一條邊使之變成平面圖)[21],問題仍然NP難。另一個相關問題是計算僅能使用直線段畫圖時,交叉數目的最小值。該最小值稱為直線交叉數(rectilinear crossing number)。該問題對於實數的存在理論是完全的。[22]
另一方面,對於固定的常數,有高效算法判定交叉數是否小於。換言之,交叉數問題是固定參數可馴順的。[23][24]但若不是常數,而是與輸入大小有關的函數,例如,則問題仍然很難。對於度數有界的圖,有高效的近似算法能夠近似計算交叉數。[25]實務上,常使用啟發式算法,例如從空圖開始,逐條邊加入,使得每次產生的交叉數儘可能小。直線交叉數分布式计算計劃(Rectilinear Crossing Number project)使用了此類算法。[26]
交叉數不等式
此種邊數、頂點數與交叉數的關係,最早由奧伊陶伊·米克洛什、瓦茨拉夫·赫瓦塔爾、蒙提·紐邦、塞邁雷迪·安德烈四人[27]和湯姆森·雷頓[28]分別獨立發現,稱為交叉數不等式或交叉數引理。不等式的上述版本是為伊爾·艾克曼(Eyal Ackerman)的結果,其中常數為截至2019年所知最優。[29]条件中的常數也可以縮少至更佳的,但代價是要換成較差的。[27][28]
雷頓之所以研究交叉數,是為了理論計算機科學中,超大型積體電路設計方面的應用。[28]其後,Székely 發現交叉數不等式用在關聯幾何方面,能夠簡短證明一些重要定理,例如塞邁雷迪-特羅特定理和貝克定理。[30]塔馬爾·戴伊類似地證明了幾何k-集數的上界。[31]
變式
若僅允許用直線段畫邊,而非任意曲線,則一些圖需要更多交叉才能畫出。對於此類畫法,交叉數目的最小可能值稱為直線交叉數。直線交叉數必不小於交叉數,甚至對某些圖而言,直線交叉數嚴格大於交叉數。完全圖至的直線交叉數依序為(OEIS數列A014540)。已知直至的直線交叉數,而則可能需要7233或7234個交叉。直線交叉數分布式计算計劃(Rectilinear Crossing Number project)收集了更多數據。[26]
若一個圖有畫法使得每條邊至多個交叉,但不能更少,則稱為其局部交叉數(local crossing number)。若圖有畫法使每條邊至多個交叉,則稱其為-平面圖(-planar)。[32]
其他變式包括兩兩相交數(pairwise crossing number,即任何畫法中,有交叉的邊對數目的最小可能值)和奇相交數(odd crossing number,即任何畫法中,交叉次數恰為奇數的邊對數目的最小可能值)。奇相交數不大於兩兩相交數,兩兩相交數也不大於相交數。然而,哈納尼-塔特定理說明,若這三個數中有任何一個為零,則皆為零。[6] Schaefer (2014, 2018)綜述了許多變式。[33][34]
參考
- Purchase, Helen C.; Cohen, Robert F.; James, Murray I. Brandenburg, Franz-Josef , 编. . Lecture Notes in Computer Science 1027. Springer: 435–446. 1995. doi:10.1007/BFb0021827
 .
. |contribution=被忽略 (帮助). - Turán, P. . Journal of Graph Theory. 1977, 1: 7–9. doi:10.1002/jgt.3190010105.
- Bronfenbrenner, Urie. . Sociometry. 1944, 7 (3): 283–289. JSTOR 2785096. doi:10.2307/2785096.
The arrangement of subjects on the diagram, while haphazard in part, is determined largely by trial and error with the aim of minimizing the number of intersecting lines.
- Scheinerman, Edward R.; Wilf, Herbert S. . American Mathematical Monthly. 1994, 101 (10): 939–943. JSTOR 2975158. doi:10.2307/2975158.
- Garey, M. R.; Johnson, D. S. . SIAM Journal on Algebraic and Discrete Methods. 1983, 4 (3): 312–316. MR 0711340. doi:10.1137/0604033.
- Pach, J.; Tóth, G. : 617–626. 1998. doi:10.1109/SFCS.1998.743512.
|contribution=被忽略 (帮助). - de Klerk, E.; Maharry, J.; Pasechnik, D. V.; Richter, B.; Salazar, G. . SIAM Journal on Discrete Mathematics. 2006, 20 (1): 189–202 [2021-06-23]. S2CID 1509054. arXiv:math/0404142
 . doi:10.1137/S0895480104442741. (原始内容存档于2021-06-28).
. doi:10.1137/S0895480104442741. (原始内容存档于2021-06-28). - Pach, János; Sharir, Micha. . . Mathematical Surveys and Monographs 152. American Mathematical Society. 2009: 126–127.
- Zarankiewicz, K. . Fundamenta Mathematicae. 1954, 41: 137–145. doi:10.4064/fm-41-1-137-145
 .
. - Guy, Richard K. . . Academic Press, New York. 1969: 63–69. MR 0253931..
- Guy, R. K. . Nabla (Bulletin of the Malayan Mathematical Society). 1960, 7: 68–72.
- Saaty, T.L. . Proceedings of the National Academy of Sciences of the United States of America. 1964, 52 (3): 688–690. Bibcode:1964PNAS...52..688S. PMC 300329
 . PMID 16591215. doi:10.1073/pnas.52.3.688.
. PMID 16591215. doi:10.1073/pnas.52.3.688. - Pan, Shengjun; Richter, R. Bruce. . Journal of Graph Theory. 2007, 56 (2): 128–134. MR 2350621. doi:10.1002/jgt.20249..
- Barát, János; Tóth, Géza. . 2009. arXiv:0909.0413
 [math.CO].
[math.CO]. - Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Pegg, E. T.; Exoo, G. . Mathematica Journal. 2009, 11 (2). doi:10.3888/tmj.11.2-2.
- Sloane, N.J.A. (编). . The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- Haythorpe, Michael; Newcombe, Alex, , 2018, arXiv:1804.10336

- Exoo, G. . [2021-06-24]. (原始内容存档于2021-06-24).
- Hliněný, P. . Journal of Combinatorial Theory. Series B. 2006, 96 (4): 455–471. MR 2232384. doi:10.1016/j.jctb.2005.09.009.
- Cabello S. and Mohar B. . SIAM Journal on Computing. 2013, 42 (5): 1803–1829. S2CID 6535755. arXiv:1203.5944
 . doi:10.1137/120872310.
. doi:10.1137/120872310. - Schaefer, Marcus. (PDF). Graph Drawing, 17th International Symposium, GS 2009, Chicago, IL, USA, September 2009, Revised Papers. Lecture Notes in Computer Science 5849. Springer-Verlag: 334–344. 2010 [2020-11-04]. ISBN 978-3-642-11804-3. doi:10.1007/978-3-642-11805-0_32
 . (原始内容存档 (PDF)于2021-06-26)..
. (原始内容存档 (PDF)于2021-06-26).. - Grohe, M. . Journal of Computer and System Sciences. 2005, 68 (2): 285–302. MR 2059096. arXiv:cs/0009010
 . doi:10.1016/j.jcss.2003.07.008.
. doi:10.1016/j.jcss.2003.07.008. - Kawarabayashi, Ken-ichi; Reed, Bruce. . Proceedings of the 29th Annual ACM Symposium on Theory of Computing: 382–390. 2007. ISBN 978-1-59593-631-8. doi:10.1145/1250790.1250848.
- Even, Guy; Guha, Sudipto; Schieber, Baruch. . SIAM Journal on Computing. 2003, 32 (1): 231–252. doi:10.1137/S0097539700373520.
- Oswin Aichholzer. . (原始内容存档于2012-12-30)., and Rectilinear Crossing Number (页面存档备份,存于) on the Institute for Software Technology at Graz, University of Technology (2009).
- Ajtai, M.; Chvátal, V.; Newborn, M.; Szemerédi, E. . Theory and Practice of Combinatorics. North-Holland Mathematics Studies 60: 9–12. 1982. MR 0806962.
- Leighton, T. . Foundations of Computing Series. Cambridge, MA: MIT Press. 1983.
- Ackerman, Eyal. (PDF). 2013. (原始内容 (PDF)存档于2014-07-14).
- Székely, L. A. . Combinatorics, Probability and Computing. 1997, 6 (3): 353–358. MR 1464571. doi:10.1017/S0963548397002976.
- Dey, T. K. . Discrete and Computational Geometry. 1998, 19 (3): 373–382. MR 1608878. doi:10.1007/PL00009354
 .
. - Ringel, Gerhard. . Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg. 1965, 29 (1–2): 107–117. MR 0187232. S2CID 123286264. doi:10.1007/BF02996313 (德语).
- Schaefer, Marcus. . The Electronic Journal of Combinatorics. 2014. DS21 [2021-06-25]. (原始内容存档于2021-06-29).
- Schaefer, Marcus. . CRC Press. 2018.